方法一:暴力匹配 (Brute Force)
暴力解法虽然时间复杂度高,但是思路清晰、编写简单,因为编写的正确性高,完全可以使用暴力匹配算法检验我们编写的算法的正确性。
(这里就不展示暴力匹配的写法了,实际上是我很懒。)
方法二:中心扩散法
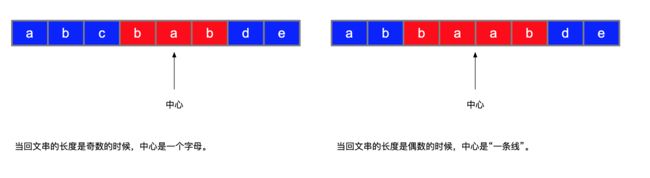
中心扩散法的想法很简单:遍历每一个索引,以这个索引为中心,利用“回文串”中心对称的特点,往两边扩散,看最多能扩散多远。要注意一个细节:回文串的长度可能是奇数,也可能是偶数。
我们完全可以设计一个方法,兼容以上两种情况:
1、如果传入重合的索引编码,进行中心扩散,此时得到的最长回文子串的长度是奇数;
2、如果传入相邻的索引编码,进行中心扩散,此时得到的最长回文子串的长度是偶数。
参考代码 1:
具体编码细节在以下的代码的注释中体现。
class Solution:
def longestPalindrome(self, s):
size = len(s)
if size == 0:
return ''
# 至少是 1
longest_palindrome = 1
longest_palindrome_str = s[0]
for i in range(size):
palindrome_odd, odd_len = self.__center_spread(s, size, i, i)
palindrome_even, even_len = self.__center_spread(s, size, i, i + 1)
# 当前找到的最长回文子串
cur_max_sub = palindrome_odd if odd_len >= even_len else palindrome_even
if len(cur_max_sub) > longest_palindrome:
longest_palindrome = len(cur_max_sub)
longest_palindrome_str = cur_max_sub
return longest_palindrome_str
def __center_spread(self, s, size, left, right):
"""
left = right 的时候,此时回文中心是一条线,回文串的长度是奇数
right = left + 1 的时候,此时回文中心是任意一个字符,回文串的长度是偶数
"""
l = left
r = right
while l >= 0 and r < size and s[l] == s[r]:
l -= 1
r += 1
return s[l + 1:r], r - l - 1
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len == 0) {
return "";
}
int longestPalindrome = 1;
String longestPalindromeStr = s.substring(0, 1);
for (int i = 0; i < len; i++) {
String palindromeOdd = centerSpread(s, len, i, i);
String palindromeEven = centerSpread(s, len, i, i + 1);
String maxLen = palindromeOdd.length() > palindromeEven.length() ? palindromeOdd : palindromeEven;
if (maxLen.length() > longestPalindrome) {
longestPalindrome = maxLen.length();
longestPalindromeStr = maxLen;
}
}
return longestPalindromeStr;
}
private String centerSpread(String s, int len, int left, int right) {
int l = left;
int r = right;
while (l >= 0 && r < len && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 这里要特别小心,跳出 while 循环的时候,是第 1 个满足 s.charAt(l) != s.charAt(r) 的时候
// 所以,不能取 l,不能取 r
return s.substring(l + 1, r);
}
}
复杂度分析:
- 时间复杂度:。
- 空间复杂度:。
方法三:动态规划(推荐)
推荐理由:暴力解法太 naive,中心扩散不普适,Manacher 就更不普适了,是专门解这个问题的方法。而用动态规划我认为是最有用的,可以帮助你举一反三的方法。
补充说明:Manacher 算法有兴趣的朋友们可以了解一下,有人就借助它的第一步字符串预处理思想,解决了 LeetCode 第 4 题。因此以上推荐仅代表个人观点。
解决这类 “最优子结构” 问题,可以考虑使用 “动态规划”:
1、定义 “状态”;
2、找到 “状态转移方程”。
记号说明: 下文中,使用记号 s[l, r] 表示原始字符串的一个子串,l、r 分别是区间的左右边界的索引值,使用左闭、右闭区间表示左右边界可以取到。举个例子,当 s = 'babad' 时,s[0, 1] = 'ba' ,s[2, 4] = 'bad'。
1、定义 “状态”,这里 “状态”数组是二维数组。
dp[l][r] 表示子串 s[l, r](包括区间左右端点)是否构成回文串,是一个二维布尔型数组。即如果子串 s[l, r] 是回文串,那么 dp[l][r] = true。
2、找到 “状态转移方程”。
首先,我们很清楚一个事实:
1、当子串只包含 个字符,它一定是回文子串;
2、当子串包含 2 个以上字符的时候:如果
s[l, r]是一个回文串,例如“abccba”,那么这个回文串两边各往里面收缩一个字符(如果可以的话)的子串s[l + 1, r - 1]也一定是回文串,即:如果dp[l][r] == true成立,一定有dp[l + 1][r - 1] = true成立。
根据这一点,我们可以知道,给出一个子串 s[l, r] ,如果 s[l] != s[r],那么这个子串就一定不是回文串。如果 s[l] == s[r] 成立,就接着判断 s[l + 1] 与 s[r - 1],这很像中心扩散法的逆方法。
事实上,当 s[l] == s[r] 成立的时候,dp[l][r] 的值由 dp[l + 1][r - l] 决定,这一点也不难思考:当左右边界字符串相等的时候,整个字符串是否是回文就完全由“原字符串去掉左右边界”的子串是否回文决定。但是这里还需要再多考虑一点点:“原字符串去掉左右边界”的子串的边界情况。
1、当原字符串的元素个数为 个的时候,如果左右边界相等,那么去掉它们以后,只剩下 个字符,它一定是回文串,故原字符串也一定是回文串;
2、当原字符串的元素个数为 个的时候,如果左右边界相等,那么去掉它们以后,只剩下 个字符,显然原字符串也一定是回文串。
把上面两点归纳一下,只要 s[l + 1, r - 1] 至少包含两个元素,就有必要继续做判断,否则直接根据左右边界是否相等就能得到原字符串的回文性。而“s[l + 1, r - 1] 至少包含两个元素”等价于 l + 1 < r - 1,整理得 l - r < -2,或者 r - l > 2。
综上,如果一个字符串的左右边界相等,以下二者之一成立即可:
1、去掉左右边界以后的字符串不构成区间,即“ s[l + 1, r - 1] 至少包含两个元素”的反面,即 l - r >= -2,或者 r - l <= 2;
2、去掉左右边界以后的字符串是回文串,具体说,它的回文性决定了原字符串的回文性。
于是整理成“状态转移方程”:
dp[l, r] = (s[l] == s[r] and (l - r >= -2 or dp[l + 1, r - 1]))
或者
dp[l, r] = (s[l] == s[r] and (r - l <= 2 or dp[l + 1, r - 1]))
编码实现细节:因为要构成子串 l 一定小于等于 r ,我们只关心 “状态”数组“上三角”的那部分取值。理解上面的“状态转移方程”中的 (r - l <= 2 or dp[l + 1, r - 1]) 这部分是关键,因为 or 是短路运算,因此,如果收缩以后不构成区间,那么就没有必要看继续 dp[l + 1, r - 1] 的取值。
读者可以思考一下:为什么在动态规划的算法中,不用考虑回文串长度的奇偶性呢。想一想,答案就在状态转移方程里面。
具体编码细节在代码的注释中已经体现。
参考代码 2:
class Solution:
def longestPalindrome(self, s: str) -> str:
size = len(s)
if size <= 1:
return s
# 二维 dp 问题
# 状态:dp[l,r]: s[l:r] 包括 l,r ,表示的字符串是不是回文串
# 设置为 None 是为了方便调试,看清楚代码执行流程
dp = [[False for _ in range(size)] for _ in range(size)]
longest_l = 1
res = s[0]
# 因为只有 1 个字符的情况在最开始做了判断
# 左边界一定要比右边界小,因此右边界从 1 开始
for r in range(1, size):
for l in range(r):
# 状态转移方程:如果头尾字符相等并且中间也是回文
# 在头尾字符相等的前提下,如果收缩以后不构成区间(最多只有 1 个元素),直接返回 True 即可
# 否则要继续看收缩以后的区间的回文性
# 重点理解 or 的短路性质在这里的作用
if s[l] == s[r] and (r - l <= 2 or dp[l + 1][r - 1]):
dp[l][r] = True
cur_len = r - l + 1
if cur_len > longest_l:
longest_l = cur_len
res = s[l:r + 1]
# 调试语句
# for item in dp:
# print(item)
# print('---')
return res
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len <= 1) {
return s;
}
int longestPalindrome = 1;
String longestPalindromeStr = s.substring(0, 1);
boolean[][] dp = new boolean[len][len];
// abcdedcba
// l r
// 如果 dp[l, r] = true 那么 dp[l + 1, r - 1] 也一定为 true
// 关键在这里:[l + 1, r - 1] 一定至少有 2 个元素才有判断的必要
// 因为如果 [l + 1, r - 1] 只有一个元素,不用判断,一定是回文串
// 如果 [l + 1, r - 1] 表示的区间为空,不用判断,也一定是回文串
// [l + 1, r - 1] 一定至少有 2 个元素 等价于 l + 1 < r - 1,即 r - l > 2
// 写代码的时候这样写:如果 [l + 1, r - 1] 的元素小于等于 1 个,即 r - l <= 2 ,就不用做判断了
// 因为只有 1 个字符的情况在最开始做了判断
// 左边界一定要比右边界小,因此右边界从 1 开始
for (int r = 1; r < len; r++) {
for (int l = 0; l < r; l++) {
// 区间应该慢慢放大
// 状态转移方程:如果头尾字符相等并且中间也是回文
// 在头尾字符相等的前提下,如果收缩以后不构成区间(最多只有 1 个元素),直接返回 True 即可
// 否则要继续看收缩以后的区间的回文性
// 重点理解 or 的短路性质在这里的作用
if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1][r - 1])) {
dp[l][r] = true;
if (r - l + 1 > longestPalindrome) {
longestPalindrome = r - l + 1;
longestPalindromeStr = s.substring(l, r + 1);
}
}
}
}
return longestPalindromeStr;
}
}
写完代码以后,请读者在纸上写下代码运行的流程,以字符串 'babad' 为例:
(草稿太潦草了,大家将就看吧,懒得绘图了,原因是太麻烦,并且我觉得展示手写草稿可能更有意义一些。)
说明:上面示例代码填写 dp 数组(二维状态数组)是按照“从左到右、从上到下”的方向依次填写的(你不妨打开我上面的 Python 示例代码中的调试语句运行一下验证),当 “ s[l + 1, r - 1] 至少包含两个元素” 即 r - l > 2 时,dp[l, r] 的值要看 d[[l + 1, r - 1] ,即在 r - l > 2 的时候,dp[l, r] 的值看“左下角”的值,只要按照“从左到右、从上到下”的方向依次填写,当 r - l > 2 时,左下角就一定有值,这一点是动态规划算法得以有效的重要原因。
根据一个具体例子,在草稿纸上写下(绘图)代码的运行流程,有时是够加深我们对算法的理解,并且也有助于调试代码。
复杂度分析:
- 时间复杂度:。
- 空间复杂度:,二维 dp 问题,一个状态得用二维有序数对表示,因此空间复杂度是 。
方法四:Manacher 算法
维基百科中对于 Manacher 算法是这样描述的:
[Manacher(1975)] 发现了一种线性时间算法,可以在列出给定字符串中从字符串头部开始的所有回文。并且,Apostolico, Breslauer & Galil (1995) 发现,同样的算法也可以在任意位置查找全部最大回文子串,并且时间复杂度是线性的。因此,他们提供了一种时间复杂度为线性的最长回文子串解法。替代性的线性时间解决 Jeuring (1994), Gusfield (1997)提供的,基于后缀树(suffix trees)。也存在已知的高效并行算法。
Manacher 算法,被中国程序员戏称为“马拉车”算法。专门用于解决“最长回文子串”问题,时间复杂度为 ,事实上,“马拉车”算法在思想上和“KMP”字符串匹配算法有相似之处,都避免做了很多重复的工作。“KMP”算法也有一个很有意思的戏称,带有一点颜色。
挺有意思的一件事情是:我在学习“树状数组”和“Manacher 算法”的时候,都看了很多资料,但最后代码实现的时候,就只有短短十几行。
理解 Manacher 算法最好的办法,是根据查阅的关于 Manacher 算法的文章,自己在稿纸上写写画画,举一些具体的例子,这样 Manacher 算法就不难搞懂了。
Manacher 算法本质上还是中心扩散法,只不过它使用了类似 KMP 算法的技巧,充分挖掘了已经进行回文判定的子串的特点,提高算法的效率。
下面介绍 Manacher 算法的运行流程。
首先还是“中心扩散法”的思想:回文串可分为奇数回文串和偶数回文串,它们的区别是:奇数回文串关于它的“中点”满足“中心对称”,偶数回文串关于它“中间的两个点”满足“中心对称”。为了避免对于回文串字符个数为奇数还是偶数的套路。首先对原始字符串进行预处理,方法也很简单:添加分隔符。
第 1 步:对原始字符串进行预处理(添加分隔符)
我们先给出具体的例子,看看如何添加分隔符。
例1:给字符串 "level" 添加分隔符 "#"。
答:字符串 "level" 添加分隔符 "#" 以后得到:"#l#e#v#e#l#"。
例2:给字符串 "noon" 添加分隔符 "#"。
答:字符串 "noon" 添加分隔符 "#" 以后得到:"#n#o#o#n#"。
我想你已经看出来分隔符是如何添加的,下面是两点说明。
1、分隔符是一定是原始字符串中没有出现过的字符,这个分隔符的种类也只能有一个,即你不能同时添加 "#" 和 "?" 作为分隔符;
2、添加分隔符的方法是在字符串的首位置、尾位置和每个字符的“中间”都添加 个这个分隔符。可以很容易知道,如果这个字符串的长度是 len,那么添加的分隔符的个数就是 len + 1,得到的新的字符串的长度就是 2 * len + 1,显然它一定是奇数。
为什么要添加分隔符?
1、首先是正确性:添加了分隔符以后的字符串的回文性质与原始字符串是一样的(这句话不是很严谨,大家意会即可);
2、其次是避免回文串长度奇偶性的讨论(马上我们就会看到这一点是如何体现的)。
第 2 步:得到 p 数组
p 数组可以通过填表得到。以字符串 "abbabb" 为例,说明如何手动计算得到 p 数组。假设我们要填的就是下面这张表。
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | |||||||||||||
| p-1 |
第 1 行 char 数组:这个数组是原始字符串加上分隔符以后的字符构成的数组。
第 2 行 index 数组:这个数组是char 数组的索引数组,我们后面要利用到它,它的值就是索引编号,从 开始。
下面我们来看看 p 数组应该如何填写。首先我们定义“回文半径”。
回文半径:以 char[i] 作为回文中心,同时向左边、向右边进行“中心扩散”,直到“不能构成回文串”或“触碰到字符串边界”为止,能扩散的步数 + 1(这个 1 表示“中心”) ,即定义为 p 数组的值,也称之为“回文半径。
- 用上面的例子,我们首先填
p[0]。
以 char[0] = '#'为中心,同时向左边向右扩散,走 1 步就碰到边界了,因此“能扩散的步数”为0,“能扩散的步数 + 1 = 1”,因此 p[0] = 1;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | ||||||||||||
| p-1 |
- 下面填写
p[1]。
以 char[1] = 'a' 为中心,同时向左边向右扩散,走 1 步,左右都是 "#",构成回文子串,于是再继续同时向左边向右边扩散,左边就碰到边界了,因此“能扩散的步数”为1,“能扩散的步数 + 1 = 2”,因此 p[1] = 2;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | |||||||||||
| p-1 |
- 下面填写
p[2]。
以 char[2] = '#' 为中心,同时向左边向右扩散,走 1 步,左边是 "a",右边是 "b",不匹配,因此“能扩散的步数”为 ,“能扩散的步数 + 1 = 1”,因此 p[2] = 1;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | 1 | ||||||||||
| p-1 |
- 下面填写
p[3]。
以 char[3] = 'b' 为中心,同时向左边向右扩散,走 1 步,左右两边都是 “#”,构成回文子串,继续同时向左边向右扩散,左边是 "a",右边是 "b",不匹配,因此“能扩散的步数”为 1 ,“能扩散的步数 + 1 = 2”,因此 p[3] = 2;
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | 1 | 2 | |||||||||
| p-1 |
- 下面填写
p[4]。
以 char[4] = '#' 为中心,同时向左边向右扩散,最多可以走 4 步,左边到达边界,因此“能扩散的步数”为4,“能扩散的步数 + 1 = 5”,因此 p[4] = 5。
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | 1 | 2 | 5 | ||||||||
| p-1 |
- 继续填完 p 数组剩下的部分。
分析到这里,后面的数字不难填出,最后写成如下表格:
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 |
| p-1 |
p-1 数组很简单了,把 p 数组对应位置的值 -1 就行了。是不是觉得有点“绕”,刚才每一步要 + 1 ,现在每一步要 -1,这不是吃饱了撑的吗?你说的没错。这里得到 p 数组不过就是为了给“回文半径”一个定义而已。
即:p 数组可以称之为“回文半径数组”。
于是我们得到如下表格:
| char | # | a | # | b | # | b | # | a | # | b | # | b | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| p | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 |
| p-1 | 0 | 1 | 0 | 1 | 4 | 1 | 0 | 5 | 0 | 1 | 2 | 1 | 0 |
- p 数组的最大值是 ,对应的 “最长回文子串” 是
"#b#b#a#b#b#"; - p - 1 数组的最大值是 ,就对应了原字符串
"abbabb"的 “最长回文子串” :"bbabb"。
规律如下:
p -1 数组的最大值就是“最长回文子串”的长度。即“最大回文半径”知道了,减 1 就是原字符串的“最长回文子串”的长度。
- 可以在得到 p 数组的过程中记录这个最大值,并且记录最长回文子串。
那么如何编写程序得到 p 数组呢?其实也不难,即使用“回文串”的性质避免重复计算。下面这张图展示了这个思想:
{:width="500"}
{:align=center}
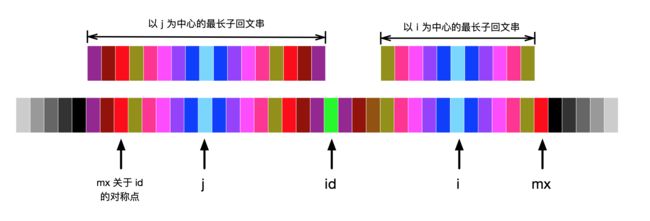
上面这张图画得仔细一点是下面这张图:
{:width="700"}
{:align=center}
这里 i 和 j 关于 id 中心对称:即 j = 2 * id - i。上面的两张图表示的意思是:p[i] 的值可以根据 p[j] 得到。因为我们遍历一个字符串的方向是“从左到右”,故数组 p 后面的值根据前面的值得来,这个思路没有问题。
接下来要介绍 id 和 mx 的含义了:
1、id :从开始到现在使用“中心扩散法”能得到的“最长回文子串”的中心的位置;
2、mx:从开始到现在使用“中心扩散法”能得到的“最长回文子串”能延伸到的最右端的位置。容易知道 mx = id + p[id]。
先从最简单的情况开始:
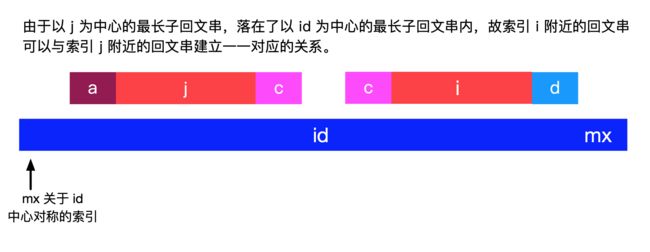
1、当 id < i < mx 的时候,此时 id 之前的 p 值都已经计算出来了,我们利用已经计算出来的 p 值来计算当前位置的 p 值。
由于以 j 为中心的最长子回文串,落在了以 id 为中心的最长子回文串内,由于 i 和 j 对称, 故索引 i 附近的回文串可以与索引 j 附近的回文串建立一一对应的关系。
- 如果
j的回文串很短,在mx关于id的对称点之前结束,一定有dp[i]=dp[j],如上图所示; - 如果
j的回文串很长,此时dp[i]的值不会超过i与mx之间的距离:mx - i,此时想一下mx是 以id为中心的最长回文子串的“最右边界”,就不难理解了,如下图所示 。
如果 p[j] 很大的话,即当 p[j] >= mx - i 的时候,以 s[j] 为中心的回文子串不一定完全包含于以 s[id] 为中心的回文子串中,但是基于对称性可知,以 s[i] 为中心的回文子串,其向右至少会扩张到 mx 的位置,也就是说 p[i] >= mx - i。至于 mx 之后的部分是否对称,就只能老老实实去匹配了。
{:width="700"}
{:align=center}
把上面说的整理一下,当 p[j] 的范围很小的时候,有 p[i] = p[j],p[i] 的值再大不过超过 mx - i :
if i < mx:
p[i] = min(p[2 * id - i], mx - i);
2、当 i >= mx 的时候,此时也只能老老实实使用“中心扩散法”来逐渐得到 p 数组的值,同时记录 id 和 mx。
以上可以合并成一行代码:
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
这一行代码拆开来看就是:
如果 mx > i, 则 p[i] = min(p[2 * id - i], mx - i),否则 p[i] = 1。
参考代码 3:
public class Solution {
/**
* 创建分隔符分割的字符串
*
* @param s 原始字符串
* @param divide 分隔字符
* @return 使用分隔字符处理以后得到的字符串
*/
private String generateSDivided(String s, char divide) {
int len = s.length();
if (len == 0) {
return "";
}
if (s.indexOf(divide) != -1) {
throw new IllegalArgumentException("参数错误,您传递的分割字符,在输入字符串中存在!");
}
StringBuilder sBuilder = new StringBuilder();
sBuilder.append(divide);
for (int i = 0; i < len; i++) {
sBuilder.append(s.charAt(i));
sBuilder.append(divide);
}
return sBuilder.toString();
}
public String longestPalindrome(String s) {
int len = s.length();
if (len == 0) {
return "";
}
String sDivided = generateSDivided(s, '#');
int slen = sDivided.length();
int[] p = new int[slen];
int mx = 0;
// id 是由 mx 决定的,所以不用初始化,只要声明就可以了
int id = 0;
int longestPalindrome = 1;
String longestPalindromeStr = s.substring(0, 1);
for (int i = 0; i < slen; i++) {
if (i < mx) {
// 这一步是 Manacher 算法的关键所在,一定要结合图形来理解
// 这一行代码是关键,可以把两种分类讨论的情况合并
p[i] = Integer.min(p[2 * id - i], mx - i);
} else {
// 走到这里,只可能是因为 i = mx
if (i > mx) {
throw new IllegalArgumentException("程序出错!");
}
p[i] = 1;
}
// 老老实实去匹配,看新的字符
while (i - p[i] >= 0 && i + p[i] < slen && sDivided.charAt(i - p[i]) == sDivided.charAt(i + p[i])) {
p[i]++;
}
// 我们想象 mx 的定义,它是遍历过的 i 的 i + p[i] 的最大者
// 写到这里,我们发现,如果 mx 的值越大,
// 进入上面 i < mx 的判断的可能性就越大,这样就可以重复利用之前判断过的回文信息了
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
if (p[i] - 1 > longestPalindrome) {
longestPalindrome = p[i] - 1;
longestPalindromeStr = sDivided.substring(i - p[i] + 1, i + p[i]).replace("#", "");
}
}
return longestPalindromeStr;
}
}
复杂度分析:
- 时间复杂度:,由于 Manacher 算法只有在遇到还未匹配的位置时才进行匹配,已经匹配过的位置不再匹配,所以对于对于字符串
S的每一个位置,都只进行一次匹配,所以算法的总体复杂度为 。 - 空间复杂度:。