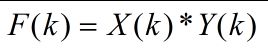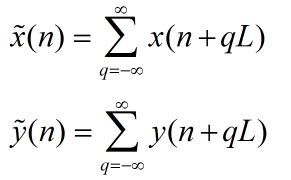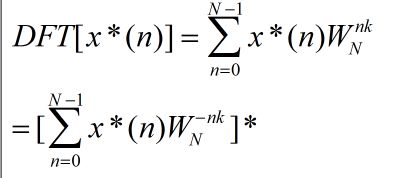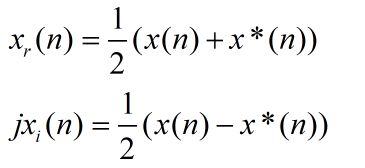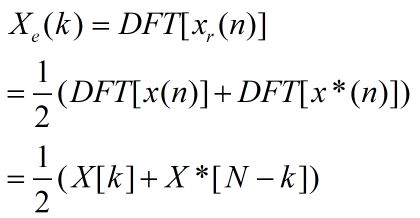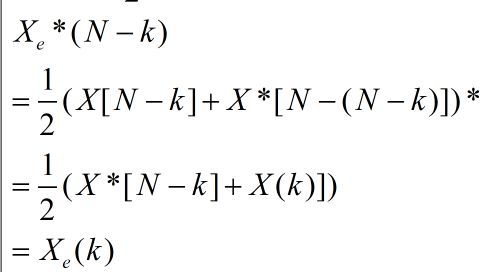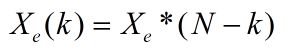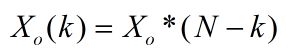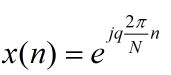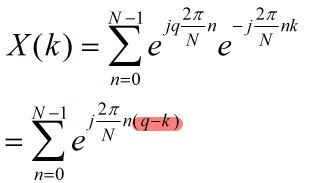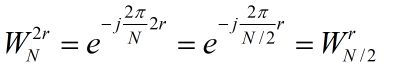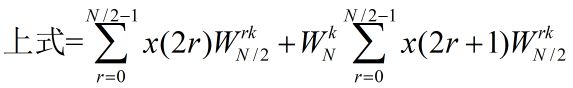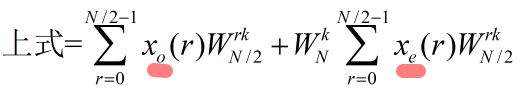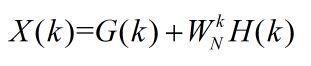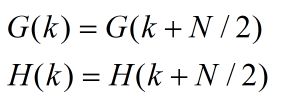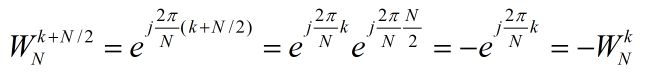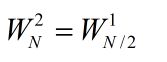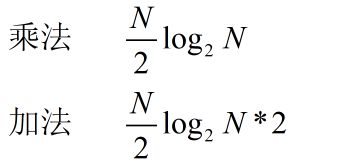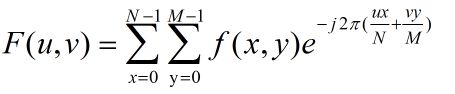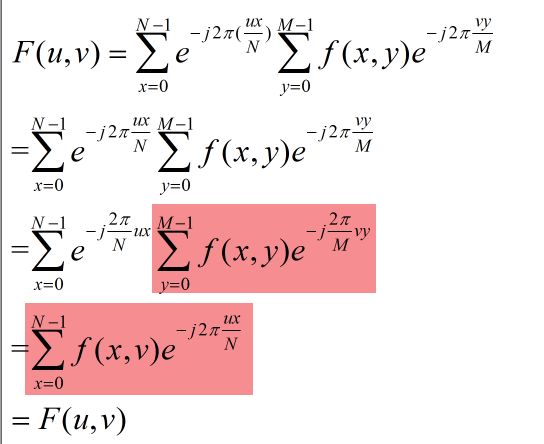因为要移植CSK得写快速傅里叶变换的算法,还是二维的,以前在pc平台上只需调用库就可以了,只是有点印象原信号和变换之后代表的是什么,但是对于离散傅里叶变换的来龙去脉忘得已经差不多了,最近要用到,于是重新来学习一遍,翻出了自己大三当时录的吴镇扬老师讲的数字信号处理的视频,DFT-FFT这里老师讲了有10讲之多,但每讲都不是很长,20分钟左右,这里记录一下学习的过程,前面的推导有点多,又打不了公式,mathtype的直接复制也不过来,截图又太麻烦,也为了自己再推导一遍,手写了前面一部分的内容。图片形式传上来。
简单说几句:DTFT有了之后为什么还要搞出来一个DFT呢,其根本原因就是因为DTFT的频域是连续的,无法用计算机进行处理。根据我们之前得到的的傅里叶变换的规律:
连续----非周期
离散----周期
周期----离散
非周期----连续
根据这四个规律,只有一种情况可以保证两个域都是离散的,那么就是周期离散的信号,对应的另外一个域是离散周期的,但是我们又知道周期的信号是没有傅里叶变换的,因为在整个Z平面是不收敛的,这就是一个问题了,讨论就从这里开始。
从DTFT到DFS
从DFS到DFT
简单的来说,DFT是针对有限长序列的,那么怎么来做DFT呢,这里的做法是找到其对应的周期延拓序列,做DFS,然后再截取主值序列。相当于是把DFS引申到有限长序列里来,之所以能够引申是因为DFS的时域和频域都是周期的,而且周期还是相同的。
上面讨论了DFT的三个性质,分别是 线性,循环移位和循环卷积,关于循环移位和循环卷积有必要说几句:
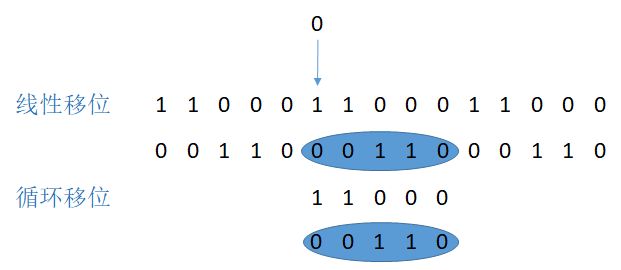
DFT的循环移位和循环卷积分别对应着DFS的线性移位和周期卷积,这两者实际上是有着很强烈的关系的,甚至在某种情况下是完全一样的:那就是当我们只关注DFS的一个周期时,循环卷积和线性卷积是一样的。(所谓循环移位就是从一端移出去的要从另一端移进来)
看个例子:
这里的根本原因在于:当我们只关注一个周期时,周期序列的线性移位和和非周期序列的循环移位的结果是完全相同的。
上面都是向右移动两个单位,如果只关注主值的话,循环移位和线性移位的结果是完全一样的。正是由于这个原因,所以才有了循环卷积,卷积里也有移位的操作,循环卷积和周期卷积来说,如果只关注一个主值序列的话,那么结果是一样的。
关于循环卷积还有一些更重要的性质。
循环卷积(针对两个有限长序列)
- 若:
则有:
主要意思:时域循环卷积相当于频域点积。 - 计算过程:
① 有限长序列构造周期序列
② 计算周期卷积
③ 周期卷积取主值
循环卷积是可以用DFT来做的,因为1的性质,如果直接用DFT来做的话,计算量实际上是要比卷积大的, 但是因为我们有FFT,所以许多情况下循环卷积还是可以通过FFT来做的,而且计算量会大大减小,特别是其中的一个序列不变的情况下(比如滤波器,那么这个滤波器只需要做一次FFT)。
这样可能又有疑问了:对于线性系统来说(比如脉冲响应),是通过线性卷积来算的,移出去就不会再移回来了,那么貌似循环卷积又没什么用了?答案肯定是否定的!,如果是这样我们讨论着半天不是白说了?实际上,在某些情况下是可以用循环卷积来计算线性卷积的,下面讨论这种情况,看下要满足什么条件。 - 有限长序列的循环卷积和线性卷积。
上面说了:循环卷积在一定条件下可以计算线性卷积。
假设有两个有限长序列:x(n)和y(n),长度分别为N,M,那么线性卷积的长度是N+M-1(算一下就知道了)。
那么我们如果对这两个序列做循环卷积呢?要做循环卷积,序列长度首先得一样,那么怎么变得一样呢?在后面添0。添多少呢?现在还不知道。
我们假设添到L(L>max(M,N)),添0对线性卷积是没有影响的,为了分析两者的循环卷积,先看其周期延拓:
那我们先把周期卷积算一下:
结论就是:周期卷积相当于线性卷积(上面红色的字打错了,我不小心把mathtype关了,懒得改了)的周期搬移。而循环卷积是周期卷积的主值序列。
这样就说明说明呢?说明周期卷积是线性卷积的周期延拓的关系,延拓的周期是L。
这时候就要关注混叠了,因为L必须足够长才能保证搬移的时候不会发生混叠,结合上面线性卷积的长度,那么L的长度最少就是L>=N+M-1,这样才不会产生混叠。这样取主值区间才能取到线性卷积的结果。
这样就可以用循环卷积做线性卷积。
共轭对称性
设x(n)的共轭复序列是x*(n).则:
DFT[x*(n)]=X*(N-K)
证明:
由于W是周期的,且周期是N,所以可以写作:
看这个结果和DFS其实是一样的,这里只不过把它移动到主值区间上罢了。
分别x(n)看实部和虚部:
根据线性变换的性质,实部和虚部分别做DFT,那么可以得到:
同理:
那么显然是有:
为什么把上面的叫做奇对称和偶对称分量呢?看下面的推导,对于偶对称来说:
即:
同理的:共轭奇对称分量为:
实际上:共轭偶对称就是实部DFT的结果,共轭奇对称是虚部DFT的结果,满足这样的关系。
那么对于纯实数序列来说,其只存在共轭偶对称部分,表明实数序列的DFT满足共轭偶对称性,利用这一特性,只要知道一半数目的X(k),就可以得到另一半,这一特点可以在DFT运算中加以利用,提高运算效率。。
还有一个例子:对于一个实数序列(长度为n)来说,其DFT是2n个点(那个虚数),数据量是增加了一倍了的,而他们之间只是线性变换而已,为什么多了这么多数据?实际上用共轭偶对称可以很好解释,实际上没有多,有一半的数据就可以通过共轭对称性得到另外一半。
另外值得一提的是:DFT的两端是对称的,即x(n)与X(K)是对称的,那么如果把频域作为原始数据,依然可以找到时域的共轭偶对称和奇对称部分。不细说了。
选频性
DFT具有选频性。
进行采样:
其中
其中q是整数,w0=2pi/N时: 其傅里叶变换为:
这个式子前面讨论过,这是n个模为1的向量,只有k=q+sN时是1,其他时候都是0,在这个主值序列里就是k=q。
这个是显而易见的,如果输入序列只有一个频率,那么对这个序列采样再进行DFT就应该只有一个频率是有值的。
当如数频率是qw0时,变换X(k)的N个值中只有X(q)=N,其余均是0,如果输入信号为若干不同频率的信号的组合,经离散傅里叶变换后,这些频率对应的X(k)应有对应输出,因此,离散傅里叶变换算法实质上对频率有选择性。
看个题:
一个余弦序列,频率是qw0,这样得到的频谱就是两条线,一个q,一个其对称位置。这也验证了刚才共轭偶对称的性质。
DFT和z变换。
DFT是DTFT频域采样的结果。
这样采样也会有问题的,就相当于通过一个栅栏来观察DTFT的结果,肯定有信息丢失,可能就会有有问题,到底采样密度怎样才是好的。
实际上从上面讨论中可以看到了,N个点的DFT是N个点,所以在频域的采样数M的条件应该是:M>=N。
证明:
这个证明的关键也是在于交换了一个积分顺序,结论是很直观的,就是 在频域采样就相当于是在时域周期延拓,那么对于一个长度为N的序列,只有当以大于N的周期去延拓时才不会发生混叠,所以频域的采样应该至少是N个点。把这个直观的结果记住,具体的证明如果要用到查书即可。
中间吴老师还讲了帕斯瓦尔定力,一些信号处理的流程,把整个知识串起来的,我快快得看了一遍。已经等不及去看FFT了。
频谱泄露这一次才真正理解了,频谱泄露就是加窗时发生的,离散周期信号要进行DFT时要进行截断,如果不是整周期截断,做DFT得到的频谱就会发生泄露,本质的原因就是周期延拓的时候就不是原先的信号了(因为没有整周期截断),这个是个充要条件。
其他的就不说了。
从DFT到FFT
DFT并不是新的算法,但是直到FFT的发现,才让DFT真正运用到工业和生活中,1965年cooley(IBM)和Tukey(MIT)提出了2FFT(2的幂次)算法。这样使得DFT的计算量提高了1,2数量级(与N有关)。这个是基2的DFT算法。
实际上还有其他的算法,一个典型的算法是:76年IBM的S.Winograd博士推导了WFTA算法,使FFT得运算再次下降很多,但是由于其用到了取模运算来映射地址,而这种寻址是非常耗时的,所有大数据的FFT都不用了,只在一些小范围内还有运用(查表方式取模),这段是吴老师科普的。
下面主要介绍基2的FFT的算法:
DFT的计算。
首先我们看下要进行n点DFT运算时要进行的计算量:
实际上这两者变换只是差了一个指数的负号和一个常数,其计算量是完全相同的。这里只讨论正变换的计算量:
一般来说,我们认为x(n),W,X(k)都是复数,那么每计算一个k,需要N的复数乘法,以及N-1个复数加法(N个相加),一共需要计算N各k,所以一次N点的DFT要用到:
N*N的复数乘法和N(N-1)的复数加法。
而实际上复数的乘法和加法都是通过实数完成的,每一次复数乘法需要4次实数乘法和2次实数加法,所以最后换算到实数计算量:
每一次N点的DFT所需的计算量:4N^2次乘法和2N(2N-1)次加法。
DFT有几个特点:
-
系数W是周期的和对称的。
- 计算量是正比于N^2的,所以当N比较小的时候,计算量是可以接受的,所以一个思路就是把大的序列拆成小的序列。
基2的FFT主要有两种,按时间抽取的和按频率抽取的。重点说按时间抽取的,即按照n抽取的。
按时间抽取的基2FFT
首先我们假定序列x(n)长度是2^M,不够的话补零。
带入求DFT得公式之中:
由于:
则有:
这两个求和实际上还是DFT,分别是偶数序列和奇数序列的,点数均是N/2。然后加权求和。
根据上面分析的,则有:其实我一开始很纠结这块关于括号里的2r,这个其实不要被表面蒙骗了,虽然是2r,但是在这个序列里还是代表的是第r个数,所有求和符号与W里都化简成了r,都是从0开始到N/2的自然数。
其中两个x分别是偶数序列和技术序列,这样就很明显了,就是两个分离的DFT。
但是我们知道,N点对应的DFT的点数是N点,这两个都是N/2的,那么对应变换再求和还是只有N/2个点啊,但是X(k)应该是有N个点的,怎么会少了一半呢?带着这个疑问再往下看吧。
其中G(k)和H(k)分别代表偶数序列和奇数序列的DFT。都是以N/2为周期的。
所以:
前面证明过:
所以有:
所以N点的DFT可以拆成奇偶两部分,然后分别以不同形式加权(加和减)获得,前一半的k做加法,后一半做减法,这样就能得到N点的DFT结果。
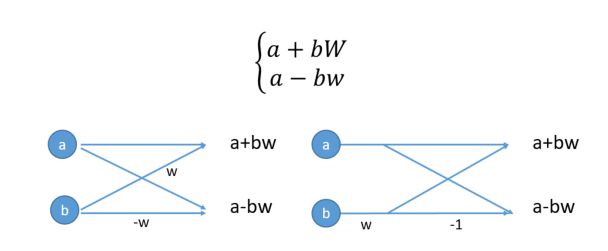
如果我们简化用a,b,w分别表示上面的式子,那么我们需要计算两个式子:
画的这个图就是简化的地方:右边的计算只需要一次复数乘法(wb只需要计算一次)和两次复数加法。这就是一个蝶形运算。
到这里归纳一下:一个偶数点的DFT可以分成奇偶两部分,然后通过蝶形运算加权起来,我们这里取得N是2的m次幂,所以这样我们可以按照这个思想一致分下去,一直分到2为止。
先看一个简单的:
以N=8为例,做一次奇偶分解,然后通过蝶形运算组合起来:
这个很好理解吧,还可以再拆一次,拆的过程省略了,直接看计算的结果:
x的下标是分解的结果,x1是第一次分解的偶数,x2是第一次分解的奇数,x3是x1分解的偶数,x4是x1分解的奇数,以此类推。
稍微有疑问的一点可能是做完N/4的DFT之后的因子为什么是W(N-0)和W(N-2),这是因为:
这样就很清楚了。这样表示是把所有的W因子都用N为底的来表示。写起来好看也好算
2点的DFT本身就是一个蝶形运算了,相当于再分解了一次:
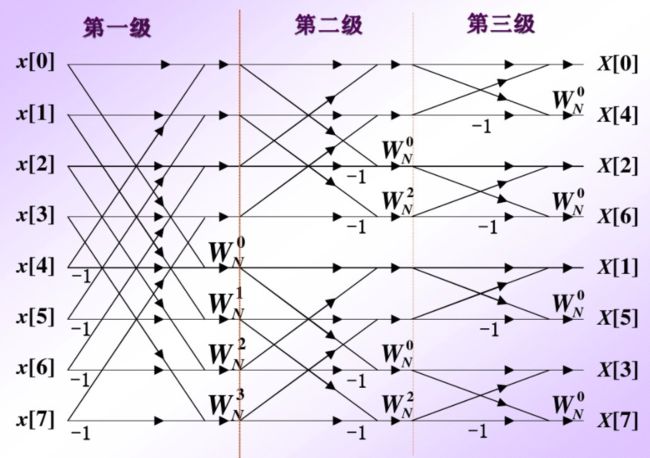
这就是N等于8时按时间抽取FFT的运算流程图。
所以2的整数次方的DFT完全可以由蝶形运算计算,这样就大大降低了计算量。
现在就只剩下一个问题了:如何分奇偶?如果要通过除以2判断余数的话,那么数据量大的时候这种算法效率还是不高的。
下面介绍时间抽取FFT的四个特点,根据这些特点才可以设计出高效的计算机计算算法。
-
蝶形运算
2^m点的数据,共有M排蝶形运算,有N/2个蝶形(每两个数据一次蝶形),每一次蝶形1次复数乘法,2次加法,m是N以2为底的对数,所以N点的计算量为:
这里写的都是复数的运算量。 - 原位计算
这是很好理解的,这是个单向的运算,一旦算到第二排,第一排所有的数据就不再需要了,这样的好处是一个流水操作,跟前面的是没有关系的,可以节省了很多的运算空间。 -
序数重排(乱序)
在进行蝶形运算之前,是要把原始自然顺序的数据要重新排列,这个如果没有规律耗时的话这个算法就不会成功了。
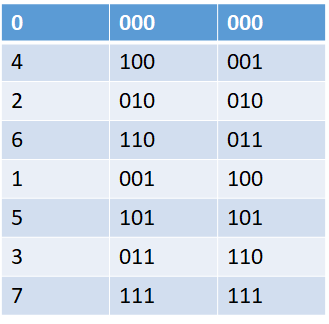
值得庆幸的是,基2fft的这种乱序是有规律的。以这八点为例,我们把这种乱序的序号用三位二进制表示,然后再中心对称,看看结果是什么:
看最右边的一列是什么?就是序列的顺序标号,这种操作显然是可逆的。也就是说我把自然顺序的地址反过来就可以得到新的地址,这种地址的规律性可以称作按位翻转的地址。
一些专门为信号处理的处理器内置了按位翻转单元,能够以更高的效率来进行fft运算。
实际上这个规律不是说硬是这样发现的,而是隐含在蝶形运算里的。第一次分奇偶的时候是按照最低位分的,分好的奇偶在各自的序列里同样是按照奇偶来分的。这样就是一位一位来分,反过来就相当于是从高位来。 - 蝶形的类型成倍增加
蝶形的类型主要区别在W上,取数的间隔也是这样的一个规律。
这样的话,有了这四个规律,基2FFT的整个计算就很明了了。不够2的基数是可以添0处理的,这样还能改进栅栏效应。
关于基于频率抽取的算法没有仔细关注,只是简单的看了一下,感觉和按照时间抽取整个过程是反过来的。计算量也是完全一样的,时间顺序不用重排,但是频谱的顺序是乱序的,依然需要重排。而且乱序的规律都是一样的。原位计算也是满足的,蝶形的类型是随着次数的增加而减少。
还有一个更有意思的,如果把这整个计算系统当做一个系统的话,把输入当输出,输出当输入,当中的箭头全部反向,这就是同一个东西了。我找了一张图,可以看下。
吴老师讲:这个在信号流图中被称作转置定理,如果有兴趣的话可以去看看这个,我这里不细究了。
当然还是有其他的算法,基4的,N是组合数的,如果有兴趣也可以找来研究,我了解到这里就足够了。
总结:至此为止,从DTFT开始,如何一步一步得来到DFT以及怎样得到FFT的算法,我觉得已经总结得很清楚了,中间有大量的公式都是在mathtype上敲好然后截图过来的。还是花费了一定的心力,这种经典的理论如果看进去了就真的和一本好书一样,常看常新,经常都会有新的理解。下面应该还会写编程实现和二维的怎么来算。如果写了链接贴在这里。
从一维到二维
本来想重写一篇的,后来发现从一维到二维的推导是如此的明了和简单,就放在这里了:
信号中的fft大都是一维的,图像是二维信号,在图像中的频谱分析都是一维的,所以有必要对二维的DFT进行分析。在看这个之前,应该要对一维的DFT有充分的了解,可以看这里。
二维DFT的公式是怎么来的就不仔细推导了,只是看着公式推导一下和一维DFT之间的关系。
二维DFT
对于M行N列的矩阵,我们定义其DFT为:我们按照其求和顺序写开:
当依照求和顺序把不相关的提出去的时候就很容易发现,这实际上是可以分解成两组DFT的,可以对每一列先进行DFT,然后得到的结果还是这么大的矩阵,然后在在此基础上进行行DFT,这样得到的最终结果就是二维矩阵的DFT,二维DFT我们也是依照这个思路去算的,DSP的函数库里提供了一维的DFT运算函数,应该是效率比较高的,可以去借助这个实现二维离散傅里叶变换。
1-18,修改了些错别字。