- 计算机木马详细编写思路
小熊同学哦
php开发语言木马木马思路
导语:计算机木马(ComputerTrojan)是一种恶意软件,通过欺骗用户从而获取系统控制权限,给黑客打开系统后门的一种手段。虽然木马的存在给用户和系统带来严重的安全风险,但是了解它的工作原理与编写思路,对于我们提高防范意识、构建更健壮的网络安全体系具有重要意义。本篇博客将深入剖析计算机木马的详细编写思路,以及如何复杂化挑战,以期提高读者对计算机木马的认识和对抗能力。计算机木马的基本原理计算机木
- 非对称加密算法原理与应用2——RSA私钥加密文件
私语茶馆
云部署与开发架构及产品灵感记录RSA2048私钥加密
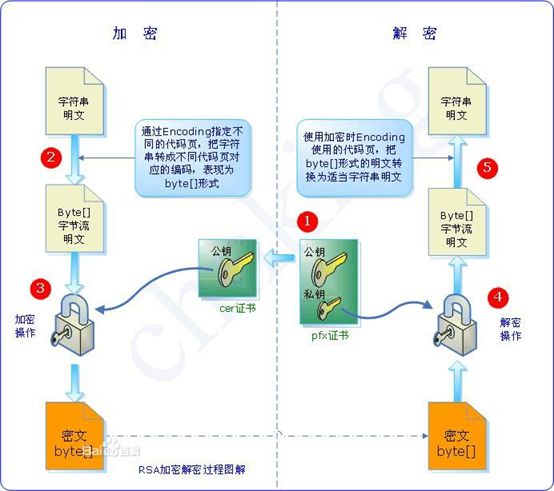
作者:私语茶馆1.相关章节(1)非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对,并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容,包括从密钥库或文件中读取私钥,并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件,只能由该私钥对应的公钥来解密。
- 非对称加密算法————RSA理论及详情
hu19930613
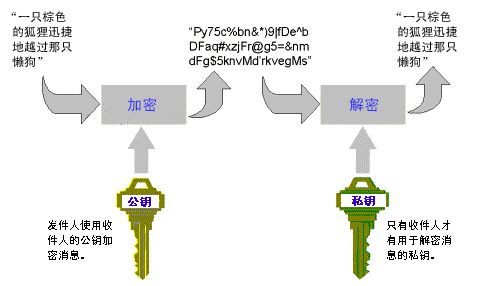
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- 【加密算法基础——对称加密和非对称加密】
XWWW668899
网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法,各自有不同的特点和用途。以下是详细比较:1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快,适合处理大量数据。实现:算法相对简单,计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
- 【加密算法基础——RSA 加密】
XWWW668899
网络服务器笔记python
RSA加密RSA(Rivest-Shamir-Adleman)加密是非对称加密,一种广泛使用的公钥加密算法,主要用于安全数据传输。公钥用于加密,私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏:R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法,并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础,使得安全通
- 信息系统安全相关概念(下)
YuanDaima2048
基础概念课程笔记安全
文章总览:YuanDaiMa2048博客文章总览上篇指路:信息系统安全相关概念(上)信息系统安全相关概念[下]信息系统风险评估安全风险评估信息系统等级保护网络安全法等级保护等级保护工作流程环境安全信息系统风险评估安全风险评估对信息系统整体安全态势的感知和对重大安全事件的预警,实现“事前能预防,事中能控制,事后能处理”。安全风险组成的四要素:信息系统资产(Asset)信息系统脆弱性(Vulnerab
- 使用游戏盾就可以保证游戏不被攻击吗?
德迅云安全小李
游戏网络服务器安全网络安全
游戏服务器不管是个人的还是企业的,被攻击都是,很常见的,在所难免的。特别是游戏新上线时,都要承受的住哪些外来压力,玩家突然猛增,被攻击等等。如果承受不住可能会直接宣布游戏倒闭。这里我们一起来说说怎么用游戏盾防御游戏服务器。首先我们要了解的一点是,什么是"游戏盾"游戏盾是针对游戏行业所推出的高度可定制的网络安全解决方案,除了能针对大型DDoS攻击(T级别)进行有效防御外,还能彻底解决游戏行业特有的T
- 构建常态化安全防线:XDR的态势感知与自动化响应机制
安胜ANSCEN
网络安全运维威胁分析自动化响应网络安全常态化安全运营
当前,网络安全威胁日益复杂多变,企业正面临前所未有的严峻挑战。为有效应对这些挑战,态势感知与自动化响应机制在提升网络安全运营效率与防御效果中扮演着至关重要的角色。它们能够实时监测网络状态,智能分析潜在威胁,并在发现异常时立即触发自动化响应流程,从而迅速遏制安全风险,保障企业数字资产的安全。态势感知网络安全的“预警雷达”态势感知,作为网络安全运营的核心组件,犹如一张无形的“预警雷达”,全面监测网络环
- Tor Browser配置方法
淡水猫.
网络安全服务器
密码学中有两种常见的加密方式:对称加密:加密和解密使用同一个秘钥,如AES、DES等算法。非对称加密:加密和解密使用不相同的密钥,这两个秘钥分别称为公钥(publickey)和私钥(privatekey)——也就是说私钥可以解开公钥加密的数据,反之亦然(很神奇的数学原理)。Tor是一个三重代理(也就是说Tor每发出一个请求会先经过Tor网络的3个节点),其网络中有两种主要服务器角色:中继服务器:负
- 【网络安全】漏洞挖掘:php代码审计
秋说
网络安全phpweb安全漏洞挖掘
未经许可,不得转载。文章目录正文正文在应用程序中,通过一个JavaScript注释发现了一个备份ZIP文件。解压后,获取了应用程序的代码,其中包含如下代码片段:代码首先检查变量$action是否等于'convert',如果是,则继续执行。随后对传入的变量$data使用trim()函数去除两端空白字符,并使用eval()函数执行$data的内容。显然,代码对$data没有进行任何过滤或验证,因此可以
- 【网络安全 | 代码审计】JFinal之DenyAccessJsp绕过
秋说
网络安全web安全java代码审计漏洞挖掘
未经许可,不得转载。文章目录前言代码审计推理绕过Tomcat解析JSP总结概念验证阐发前言JFinal是一个基于Java的轻量级MVC框架,用于快速构建Web应用程序。它的设计理念是追求极简、灵活、高效,旨在提高开发效率,减少冗余代码的编写,适合中小型项目以及对性能有较高要求的项目。在较新的JFinal版本中,默认情况下无法直接通过浏览器地址栏输入.jsp文件名来访问对应的JSP文件。也就是说,主
- 为什么需要DDos高防服务器呢?
666IDCaaa
ddos服务器网络
在当今信息化快速发展的时代,网络安全问题显得尤为重要。DDoS攻击是一种耗尽系统资源的攻击方式,可以导致正常服务请求无法得到响应。这种攻击不仅影响用户体验,还可能导致企业声誉受损、经济损失以及客户流失等严重后果。因此,选择有效的DDoS高防服务对于保护网络安全至关重要。DDoS高防服务可以通过云端清洗集群、数据库监控牵引系统等技术进行有效的削弱。这些技术能够识别并过滤恶意流量,确保正常用户能够顺利
- 都2024年了,还在问网络安全怎么入门,气得我当场脑血栓发作
网安大师兄
web安全网络安全网络安全学习
前言本人从事网路安全工作12年,曾在2个大厂工作过,安全服务、售后服务、售前、攻防比赛、安全讲师、销售经理等职位都做过,对这个行业了解比较全面。下面就开始进入正题,如何从一个萌新一步一步进入网络安全行业。正题首先,在准备进入这个行业之前,我们要问一下我们的内心,工作千千万,为什么要想进入这个行业?相信每个人的答案都不一样,有的人会说,这个行业整体上比其他行业赚钱多,有的人会说特别喜欢技术,想钻研一
- 流量牵引技术与传统防火墙的区别
666IDCaaa
ddos
在网络安全领域,流量牵引技术和传统防火墙都起着重要的作用,但它们在很多方面存在着明显的区别。一、工作原理不同传统防火墙主要是通过设置访问控制规则来过滤网络流量。它基于预先设定的策略,对进入和离开网络的数据包进行检查,根据源地址、目的地址、端口号等信息决定是否允许数据包通过。例如,企业可以设置防火墙规则,只允许特定IP地址的设备访问内部网络资源,或者禁止某些端口的流量进入,以防止潜在的攻击。而流量牵
- 网络安全测评技术与标准
坚持可信
信息安全web安全网络安全
网络安全测评是评估信息系统、网络和应用程序的安全性,以发现潜在的漏洞和威胁,并确保系统符合安全标准和政策的过程。以下是常见的网络安全测评类型:1.渗透测试(PenetrationTesting)描述:通过模拟真实的攻击,评估系统、网络和应用程序的安全性,识别和修复漏洞。目标:发现系统中的安全漏洞,评估其可能被利用的风险。方法:黑盒测试:测试人员没有系统内部信息,模拟外部攻击者。白盒测试:测试人员拥
- 2021国家开放大学计算机网络安全技术形成性考核五
chaoliang.top
国开试题网络安全网络安全
本人还会继续更新其他国家开放大学的试题,请大家多多关注,如果有什么建议,还希望大家提出来,本人也好完善本人在测试答案的时候发现,本章考试回顾结果中明明选对了答案,但是提示错误的情况,并且该题没有提示正确答案,这种情况应该是国开试题出现bug导致,请大家不要担心,如果有追求完美的同学,多答几次,可能就会避开这种题,因为出题是随机的。1.SQL注入一般可通过网页表单直接输入选择多项:对错正确答案:对2
- 如何提高网络安全意识
亿林网络安全事业部
网络web安全安全
提升网络安全意识的方法提升网络安全意识是个人和企业都需要重视的问题。以下是一些有效的方法:加强教育和培训:通过参加网络安全培训课程,学习识别网络攻击的常见迹象、安全密码的设置、不点击可疑链接等知识。建立网络安全政策:制定个人网络安全规则,如定期更改密码、不在公共网络上进行敏感操作等。定期更新系统:保持操作系统和软件程序的最新状态,及时修补安全漏洞。加强网络防护:使用防火墙、反病毒软件、入侵检测系统
- HTTPS的加密流程
a添砖Java
https网络协议http
HTTP协议采用的是明文传输,所以就存在数据被截取和修改的危险,比较有名的一件事就是2015的运营商劫持事件,所以针对HTTP协议传输的数据进行加密是非常有必要的,HTTPS就是HTTP协议的基础引入了加密,可以说HTTPS=HTTP+SSL;了解加密过程之前需要了解几个概念:明文,密文,密钥,对称加密,非对称加密明文:要传输的数据;密文:对明文进行加密就可以得到密文;密钥:对明文进行加密和解密的
- 【JAVA】数据脱敏技术(对称加密算法、非对称加密算法、哈希算法、消息认证码(MAC)算法、密钥交换算法)使用方法
来一杯龙舌兰
Javajava开发语言数据脱敏技术加密算法AES
文章目录数据脱敏的定义和目的数据脱敏的技术分类对称加密算法非对称加密算法哈希算法消息认证码(MAC)算法密钥交换算法数据脱敏的技术方案实现字符替换哈希算法(例如:SHA-3算法)消息认证码(MAC)算法(CMAC)消息认证码(MAC)算法(HMAC)对称/非对称加密实现方式(例如:AES加密算法)数据分段数据伪装更多相关内容可查看数据脱敏的定义和目的数据脱敏(DataMasking)是指对数据进行
- 学习笔记:FW内容安全概述
TKE_yinian
内容安全概述信息安全概述主要威胁关于防护简介内容安全威胁应用层威胁内容安全技术WEB安全应用安全入侵防御检测邮件安全数据安全网络安全反病毒全局环境感知沙箱检测信息安全概述•信息安全是对信息和信息系统进行保护,防止未授权的访问、使用、泄露、中断、修改、破坏并以此提供保密性、完整性和可用性。•为关键资产提供机密性、完整性和可用性(CIA三元组)保护是信息安全的核心目标。CIA(Confidential
- 安全隔离上网的有效途径:沙箱
Canon_YK
零信任防泄密源代码防泄密安全网络服务器网络安全web安全
在数字化浪潮日益汹涌的今天,网络安全成为了不可忽视的重要议题。沙箱技术作为一种高效的隔离机制,为企业和个人提供了一种在享受网络便利的同时,保障系统安全的解决方案。本文旨在深入探讨沙箱技术如何做到隔离上网,从而为用户提供一个安全、可靠的上网环境。一、沙箱技术的原理与定义沙箱技术,顾名思义,就像是在计算机系统中构建一个“沙箱”,将应用程序或系统进程的运行限制在这个“沙箱”内,使其无法访问或修改系统核心
- 2024世界技能大赛某省选拔赛“网络安全项目”B模块--数据包分析(SMB流量)
落寞的魚丶
web安全安全2024世界技能大赛选拔赛网络安全B模块SMB流量分析
2024世界技能大赛某省选拔赛“网络安全项目”B模块--数据包分析③任务二、网络数据包分析取证解析:总结:任务二、网络数据包分析取证解析:A集团的网络安全监控系统发现有恶意攻击者对集团官方网站进行攻击,并抓取了部分可疑流量包。请您根据捕捉到的流量包,搜寻出网络攻击线索,并分析黑客的恶意行为。本任务素材清单:捕获的网络数据包文件(*.pcap)请按答题卡的要求完成该部分的工作任务。序号任务要求11.
- 第十二章 虚拟局域网VLAN
电脑菜鸡
计算机网络第一阶段智能路由器网络
【基础词汇】status:状态active:活动ports:端口default:默认一、分割广播方式:物理分割:路由器逻辑分割:vlan技术二、VLAN:虚拟局域网.VLAN的优势:控制广播、增强网络安全性、简化网络管理.三、VLAN的分类.1.静态VLAN:基于端口划分.(1)指定交换机的端口属于哪个VLAN.(2)当主机连接到交换机端口上时,就被分配到了对应的VLAN中2.动态VLAN:基于M
- AttackGen - AI 网络安全事件响应测试工具,附下载链接
白帽学子
安全工具web安全安全网络安全漏洞挖掘红队
为了提高我们团队在安全活动中的响应效率,我关注到了一款叫AttackGen的工具,我们需要的是一个既能快速生成场景又能准确反映现实威胁的工具。在红蓝对抗中,我们经常要模拟各种攻击场景,以测试我们的防御水平。这不仅仅是为了“打”出个结果,更重要的是从中识别出潜在的弱点,并制定相应的修复策略。传统的做法往往需要我们手动构建这些攻击场景而AttackGen能够根据指定的威胁行为者组和组织的特征来自动生成
- 网络安全(黑客)自学
白帽子凯哥
web安全安全网络安全服务器网络
一、什么是网络安全网络安全可以基于攻击和防御视角来分类,我们经常听到的“红队”、“渗透测试”等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面性,例如Web安全技术,既有Web渗透,也有Web防御技术(WAF)。作为一个合格的网络安全工程师,应该做到攻守兼备,毕竟知己知彼,才能百战百胜。二、怎样规划网络安全如果你是一
- 网络安全学习路线图(2024版详解)
白帽子008
web安全学习安全网络安全运维
近期,大家在网上对于网络安全讨论比较多,想要学习的人也不少,但是需要学习哪些内容,按照什么顺序去学习呢?其实我们已经出国多版本的网络安全学习路线图,一直以来效果也比较不错,本次我们针对市场需求,整理了一套系统的网络安全学习路线图,供大家学习参考。希望大家按照路线图进行系统学习不仅可以更高效的完成上岸,还能够系统化学习,提升自己的后期竞争力。第一阶段:数通安全Windows系统安全1.企业资产安全规
- 云服务器如何预防黑客攻击?
云安全范德彪
网络安全负载均衡ddos服务器游戏
随着互联网科技的发展,网络安全问题日益突出,企业服务器被进犯的事情也越来越频频,怎么有用处理了中小企业DDOS进犯问题。云服务器被ddos进犯了怎么办?互联网服务器遭到大流量进犯时,用户可通过装备高防,将歹意进犯流量引向高防,对维护体系进行流量过滤清洗,再将正常流量返回服务器,确保源站正常可用。1.提高服务器防护攻击流量过大,超过服务器的防护能力,就会被打封,会出现远程不上服务器、用户掉线等情况,
- 网络安全(黑客)——自学2024
白帽子黑客-宝哥
web安全安全嵌入式硬件网络单片机
一、什么是网络安全网络安全是一种综合性的概念,涵盖了保护计算机系统、网络基础设施和数据免受未经授权的访问、攻击、损害或盗窃的一系列措施和技术。经常听到的“红队”、“渗透测试”等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。作为一个合格的网络安全工程师,应该做到攻守兼备,毕竟知己知彼,才能百战百胜。二、网络安全怎么入门安全并非孤立存在,而是建立在其计算机基础之上的应用技术。
- 2024网络安全学习路线 非常详细 推荐学习
白帽黑客-晨哥
web安全学习安全数据库php
关键词:网络安全入门、渗透测试学习、零基础学安全、网络安全学习路线首先咱们聊聊,学习网络安全方向通常会有哪些问题1、打基础时间太长学基础花费很长时间,光语言都有几门,有些人会倒在学习linux系统及命令的路上,更多的人会倒在学习语言上;2、知识点掌握程度不清楚对于网络安全基础内容,很多人不清楚需要学到什么程度,囫囵吞枣,导致在基础上花费太多时间;看到很多小伙伴,买了HTML,PHP,数据库,计算机
- 入门网络安全工程师要学习哪些内容
白帽黑客2659
web安全学习安全网安入门网络安全
大家都知道网络安全行业很火,这个行业因为国家政策趋势正在大力发展,大有可为!但很多人对网络安全工程师还是不了解,不知道网络安全工程师需要学什么?知了堂小编总结出以下要点。网络安全工程师是一个概称,学习的东西很多,具体学什么看自己以后的职业定位。如果你以后想成为安全产品工程师,学的内容侧重点就和渗透测试工程师不一样,如果你想成为安全开发工程师,学的侧重点就和安全运维工程师不一样。网络安全工程师学的东
- C/C++Win32编程基础详解视频下载
择善Zach
编程C++Win32
课题视频:C/C++Win32编程基础详解
视频知识:win32窗口的创建
windows事件机制
主讲:择善Uncle老师
学习交流群:386620625
验证码:625
--
- Guava Cache使用笔记
bylijinnan
javaguavacache
1.Guava Cache的get/getIfPresent方法当参数为null时会抛空指针异常
我刚开始使用时还以为Guava Cache跟HashMap一样,get(null)返回null。
实际上Guava整体设计思想就是拒绝null的,很多地方都会执行com.google.common.base.Preconditions.checkNotNull的检查。
2.Guava
- 解决ora-01652无法通过128(在temp表空间中)
0624chenhong
oracle
解决ora-01652无法通过128(在temp表空间中)扩展temp段的过程
一个sql语句后,大约花了10分钟,好不容易有一个结果,但是报了一个ora-01652错误,查阅了oracle的错误代码说明:意思是指temp表空间无法自动扩展temp段。这种问题一般有两种原因:一是临时表空间空间太小,二是不能自动扩展。
分析过程:
既然是temp表空间有问题,那当
- Struct在jsp标签
不懂事的小屁孩
struct
非UI标签介绍:
控制类标签:
1:程序流程控制标签 if elseif else
<s:if test="isUsed">
<span class="label label-success">True</span>
</
- 按对象属性排序
换个号韩国红果果
JavaScript对象排序
利用JavaScript进行对象排序,根据用户的年龄排序展示
<script>
var bob={
name;bob,
age:30
}
var peter={
name;peter,
age:30
}
var amy={
name;amy,
age:24
}
var mike={
name;mike,
age:29
}
var john={
- 大数据分析让个性化的客户体验不再遥远
蓝儿唯美
数据分析
顾客通过多种渠道制造大量数据,企业则热衷于利用这些信息来实现更为个性化的体验。
分析公司Gartner表示,高级分析会成为客户服务的关键,但是大数据分析的采用目前仅局限于不到一成的企业。 挑战在于企业还在努力适应结构化数据,疲于根据自身的客户关系管理(CRM)系统部署有效的分析框架,以及集成不同的内外部信息源。
然而,面对顾客通过数字技术参与而产生的快速变化的信息,企业需要及时作出反应。要想实
- java笔记4
a-john
java
操作符
1,使用java操作符
操作符接受一个或多个参数,并生成一个新值。参数的形式与普通的方法调用不用,但是效果是相同的。加号和一元的正号(+)、减号和一元的负号(-)、乘号(*)、除号(/)以及赋值号(=)的用法与其他编程语言类似。
操作符作用于操作数,生成一个新值。另外,有些操作符可能会改变操作数自身的
- 从裸机编程到嵌入式Linux编程思想的转变------分而治之:驱动和应用程序
aijuans
嵌入式学习
笔者学习嵌入式Linux也有一段时间了,很奇怪的是很多书讲驱动编程方面的知识,也有很多书将ARM9方面的知识,但是从以前51形式的(对寄存器直接操作,初始化芯片的功能模块)编程方法,和思维模式,变换为基于Linux操作系统编程,讲这个思想转变的书几乎没有,让初学者走了很多弯路,撞了很多难墙。
笔者因此写上自己的学习心得,希望能给和我一样转变
- 在springmvc中解决FastJson循环引用的问题
asialee
循环引用fastjson
我们先来看一个例子:
package com.elong.bms;
import java.io.OutputStream;
import java.util.HashMap;
import java.util.Map;
import co
- ArrayAdapter和SimpleAdapter技术总结
百合不是茶
androidSimpleAdapterArrayAdapter高级组件基础
ArrayAdapter比较简单,但它只能用于显示文字。而SimpleAdapter则有很强的扩展性,可以自定义出各种效果
ArrayAdapter;的数据可以是数组或者是队列
// 获得下拉框对象
AutoCompleteTextView textview = (AutoCompleteTextView) this
- 九封信
bijian1013
人生励志
有时候,莫名的心情不好,不想和任何人说话,只想一个人静静的发呆。有时候,想一个人躲起来脆弱,不愿别人看到自己的伤口。有时候,走过熟悉的街角,看到熟悉的背影,突然想起一个人的脸。有时候,发现自己一夜之间就长大了。 2014,写给人
- Linux下安装MySQL Web 管理工具phpMyAdmin
sunjing
PHPInstallphpMyAdmin
PHP http://php.net/
phpMyAdmin http://www.phpmyadmin.net
Error compiling PHP on CentOS x64
一、安装Apache
请参阅http://billben.iteye.com/admin/blogs/1985244
二、安装依赖包
sudo yum install gd
- 分布式系统理论
bit1129
分布式
FLP
One famous theory in distributed computing, known as FLP after the authors Fischer, Lynch, and Patterson, proved that in a distributed system with asynchronous communication and process crashes,
- ssh2整合(spring+struts2+hibernate)-附源码
白糖_
eclipsespringHibernatemysql项目管理
最近抽空又整理了一套ssh2框架,主要使用的技术如下:
spring做容器,管理了三层(dao,service,actioin)的对象
struts2实现与页面交互(MVC),自己做了一个异常拦截器,能拦截Action层抛出的异常
hibernate与数据库交互
BoneCp数据库连接池,据说比其它数据库连接池快20倍,仅仅是据说
MySql数据库
项目用eclipse
- treetable bug记录
braveCS
table
// 插入子节点删除再插入时不能正常显示。修改:
//不知改后有没有错,先做个备忘
Tree.prototype.removeNode = function(node) {
// Recursively remove all descendants of +node+
this.unloadBranch(node);
// Remove
- 编程之美-电话号码对应英语单词
bylijinnan
java算法编程之美
import java.util.Arrays;
public class NumberToWord {
/**
* 编程之美 电话号码对应英语单词
* 题目:
* 手机上的拨号盘,每个数字都对应一些字母,比如2对应ABC,3对应DEF.........,8对应TUV,9对应WXYZ,
* 要求对一段数字,输出其代表的所有可能的字母组合
- jquery ajax读书笔记
chengxuyuancsdn
jQuery ajax
1、jsp页面
<%@ page language="java" import="java.util.*" pageEncoding="GBK"%>
<%
String path = request.getContextPath();
String basePath = request.getScheme()
- JWFD工作流拓扑结构解析伪码描述算法
comsci
数据结构算法工作活动J#
对工作流拓扑结构解析感兴趣的朋友可以下载附件,或者下载JWFD的全部代码进行分析
/* 流程图拓扑结构解析伪码描述算法
public java.util.ArrayList DFS(String graphid, String stepid, int j)
- oracle I/O 从属进程
daizj
oracle
I/O 从属进程
I/O从属进程用于为不支持异步I/O的系统或设备模拟异步I/O.例如,磁带设备(相当慢)就不支持异步I/O.通过使用I/O 从属进程,可以让磁带机模仿通常只为磁盘驱动器提供的功能。就好像支持真正的异步I/O 一样,写设备的进程(调用者)会收集大量数据,并交由写入器写出。数据成功地写出时,写入器(此时写入器是I/O 从属进程,而不是操作系统)会通知原来的调用者,调用者则会
- 高级排序:希尔排序
dieslrae
希尔排序
public void shellSort(int[] array){
int limit = 1;
int temp;
int index;
while(limit <= array.length/3){
limit = limit * 3 + 1;
- 初二下学期难记忆单词
dcj3sjt126com
englishword
kitchen 厨房
cupboard 厨柜
salt 盐
sugar 糖
oil 油
fork 叉;餐叉
spoon 匙;调羹
chopsticks 筷子
cabbage 卷心菜;洋白菜
soup 汤
Italian 意大利的
Indian 印度的
workplace 工作场所
even 甚至;更
Italy 意大利
laugh 笑
m
- Go语言使用MySQL数据库进行增删改查
dcj3sjt126com
mysql
目前Internet上流行的网站构架方式是LAMP,其中的M即MySQL, 作为数据库,MySQL以免费、开源、使用方便为优势成为了很多Web开发的后端数据库存储引擎。MySQL驱动Go中支持MySQL的驱动目前比较多,有如下几种,有些是支持database/sql标准,而有些是采用了自己的实现接口,常用的有如下几种:
http://code.google.c...o-mysql-dri
- git命令
shuizhaosi888
git
---------------设置全局用户名:
git config --global user.name "HanShuliang" //设置用户名
git config --global user.email "
[email protected]" //设置邮箱
---------------查看环境配置
git config --li
- qemu-kvm 网络 nat模式 (四)
haoningabc
kvmqemu
qemu-ifup-NAT
#!/bin/bash
BRIDGE=virbr0
NETWORK=192.168.122.0
GATEWAY=192.168.122.1
NETMASK=255.255.255.0
DHCPRANGE=192.168.122.2,192.168.122.254
TFTPROOT=
BOOTP=
function check_bridge()
- 不要让未来的你,讨厌现在的自己
jingjing0907
生活 奋斗 工作 梦想
故事one
23岁,他大学毕业,放弃了父母安排的稳定工作,独闯京城,在家小公司混个小职位,工作还算顺手,月薪三千,混了混,混走了一年的光阴。 24岁,有了女朋友,从二环12人的集体宿舍搬到香山民居,一间平房,二人世界,爱爱爱。偶然约三朋四友,打扑克搓麻将,日子快乐似神仙; 25岁,出了几次差,调了两次岗,薪水涨了不过百,生猛狂飙的物价让现实血淋淋,无力为心爱银儿购件大牌
- 枚举类型详解
一路欢笑一路走
enum枚举详解enumsetenumMap
枚举类型详解
一.Enum详解
1.1枚举类型的介绍
JDK1.5加入了一个全新的类型的”类”—枚举类型,为此JDK1.5引入了一个新的关键字enum,我们可以这样定义一个枚举类型。
Demo:一个最简单的枚举类
public enum ColorType {
RED
- 第11章 动画效果(上)
onestopweb
动画
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Eclipse中jsp、js文件编辑时,卡死现象解决汇总
ljf_home
eclipsejsp卡死js卡死
使用Eclipse编辑jsp、js文件时,经常出现卡死现象,在网上百度了N次,经过N次优化调整后,卡死现象逐步好转,具体那个方法起到作用,不太好讲。将所有用过的方法罗列如下:
1、取消验证
windows–>perferences–>validation
把 除了manual 下面的全部点掉,build下只留 classpath dependency Valida
- MySQL编程中的6个重要的实用技巧
tomcat_oracle
mysql
每一行命令都是用分号(;)作为结束
对于MySQL,第一件你必须牢记的是它的每一行命令都是用分号(;)作为结束的,但当一行MySQL被插入在PHP代码中时,最好把后面的分号省略掉,例如:
mysql_query("INSERT INTO tablename(first_name,last_name)VALUES('$first_name',$last_name')");
- zoj 3820 Building Fire Stations(二分+bfs)
阿尔萨斯
Build
题目链接:zoj 3820 Building Fire Stations
题目大意:给定一棵树,选取两个建立加油站,问说所有点距离加油站距离的最大值的最小值是多少,并且任意输出一种建立加油站的方式。
解题思路:二分距离判断,判断函数的复杂度是o(n),这样的复杂度应该是o(nlogn),即使常数系数偏大,但是居然跑了4.5s,也是醉了。 判断函数里面做了3次bfs,但是每次bfs节点最多