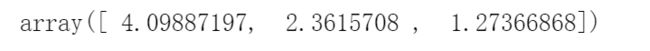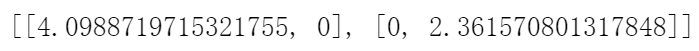03 主题模型 - LSA案例

02 主题模型 - SVD矩阵分解、LSA模型

LSA案例

假设有10个词、3个文本对应的词频TF矩阵如下：

1、只需要numpy就可以完成LSA的操作

import numpy as np

2、录入数据

a = np.array([
        [1,1,1],
        [0,1,1],
        [1,0,0],
        [0,1,0],
        [1,0,0],
        [1,0,1],
        [1,1,1],
        [1,1,1],
        [1,0,1],
        [0,2,0],
        [0,1,1]
    ]
)

3、SVD分解

numpy中的linalg库中，有专门的svd分解的函数。
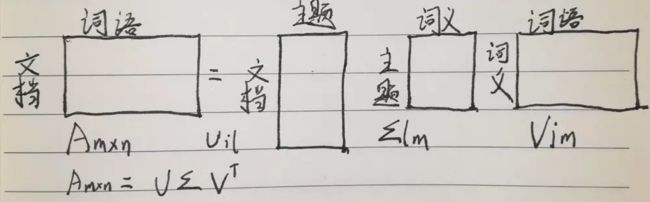
能够直接得到 U Σ V 矩阵的值。
注意：这里分解出来的不是近似值，而是完整的值。

u,sigma,v = np.linalg.svd(a)

U_il 对应第i个文本和第l个主题的相关度。
V_jm 对应第j个词和第m个词义的相关度。
Σ_lm 对应第l个主题和第m个词义的相关度

---

4、文档和主题之间的关系

假定现在3篇文本对应2个主题。现在就该获取前两列。

u[:,:2]

文档和主题之间的关系

---

5、词语和词义之间的关系

v[:,:2].T

词语和词义之间的关系

---

6、主题和词义之间的关系

sigma

s = [[sigma[0],0],[0,sigma[1]]]
s

主题和词义之间的关系

---

7、将我们上面得到的矩阵相乘，能够近似回复最初文档和词语的矩阵

np.dot(np.dot(u[:,:2],s),v[:,:2].T)

对比输出结果和原矩阵，虽然不是100%相等，但也能体现近似值

---

最后将结论描述成报告：

假定主题数为2，通过SVD降维后的三个矩阵分布为：

本例中计算的是V≈VK矩阵，但是也可以进一步计算ΣV即主题-词义关系矩阵

通过SVD矩阵分解我们可以得到文本、词与主题、语义之间的相关性，但是这个时候计算出来的内容存在负数，我们比较难解释，所以我们可以对LSI得到文本主题矩阵使用余弦相似度计算文本的相似度的计算。

最终我们得到第一个和第三个文档比较相似，和第二个文档不太相似。
备注：这个时候直接在文本主题矩阵的基础上直接应用聚类算法即可

本例中计算的是V≈VK矩阵，但是也可以进一步计算ΣV即主题-词义关系矩阵

04 主题模型 - NMF
06 主题模型 - pLSA又称pLSI - 基于概率的潜在语义分析模型