两道题都是动态规划问题,以下内容来自牛客网左神的课和书,我作为知识的搬运工,正在试图去领会程序的玄妙~~
两个题目的不同点是一个是子序列,不要求连续,另一个是子串,要求是连续的。
第一题:
首先生成动态规划表,把两个字符串一个纵对应,一个横对应,就形成了一个矩阵,这里把str1纵对应,把str2横对应。
dp[i][j]的值代表:str1[0......i]和str2[0......j]这两个子串最长公共子序列的长度是多少。
我们在看动态规划问题时要先看一个重要的概念,就是dp[i][j]的值是代表什么意义,然后再看dp[i][j]的值是怎么决策的。
首先来看动态规划表的第一排,假设str1长度为N,str2长度为M,那么第一排是dp[0][0......M-1]代表str1[0]和str2[0......j]的最长公共子序列。
例如对于dp[0][0],就是看str1第一个字符和str2第一个字符是否一样,一样的话值就为1,否则为0。接下来dp[0][1],if(str1[0]==str2[1]) dp[0][1]=1;
根据dp[i][j]的含义:str1[0......i]和str2[0......j]两个子串最长公共子序列,所以当一行有一个位置为1,那么它后面的位置值都为1,str1[0]和str2[1]的最长公共子序列长度是1,那么str1[0]和str2[1,2],str[1,2......M-1]的最长公共子序列长度肯定都是1。同样的道理,可以得出第一列的dp值。
两侧搞定之后,我们要看中间位置要怎么决策。dp[i][j]可能来自dp[i][j-1],str1[0......i]和str2[0......j]的最长公共子序列长度 >= str1[0......i]和str2[0......j-1]的最长公共子序列长度。
dp[i][j]有三种来源:
①.dp[i][j-1]
②.dp[i-1][j]
③.dp[i-1][j-1]+1:当str1[i]==str2[j],这个字符可以作为公共序列的最后一个字符。
三种可能性选择一个最大的作为dp[i][j]的值。
dp[i][j]: str1[0......i] str2[0......j]
dp[i][j-1]: str1[0......i] str2[0......j-1]
已经有了动态规划表,接下来找最长子序列:
首先找最右下角的字符,如果右下角值大于它的左边和上边的值,说明str1[N-1]==str2[M-1]且当前字符是整体公共子序列的最后一个字符,这个决策时来自于左上角,当前字符应该被包含到最长子序列中,并且向左上方移动。
如果右下角值不比它的左边和上边大,此时这个字符就不应该被包含,因为这个决策可能来自于两个方向,与哪边相等就往哪边移动。
其实根据动态规划表生成结果的过程,就是利用这张表,来还原出整个决策路径。
第二题:
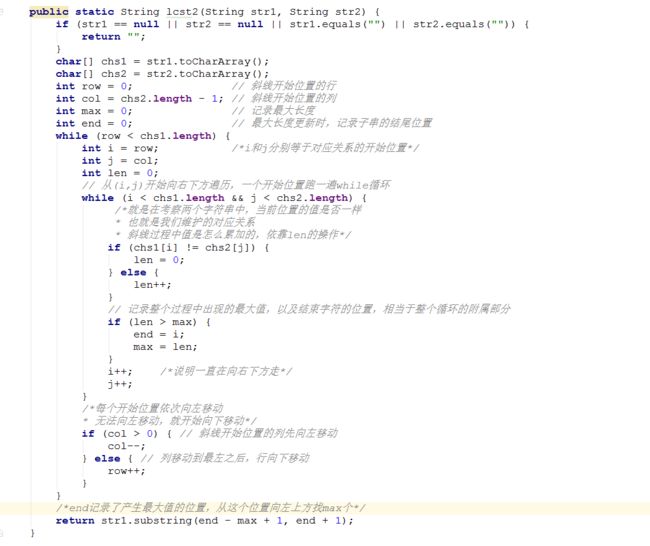
dp[i][j]:必须以str1[i]和str2[j]结尾的条件下,str1[0......i],str2[0......j]最长公共子串是多少。
①. str1[i]!=str2[j],那么dp[i][j]=0.
②. str1[i] ==str2[j], 那么dp[i][j]=dp[i-1][j-1]+1.
上述方法的空间复杂度是O(M*N)
这道题是能够做到空间复杂度O(1)的。
当前如果str1[i]!=str2[j],那么直接dp[i][j]=0。也就是说,我在当前位置做决策,我只需要我左上角的值,也就是只与斜线上左上角的值有关。
这已经不代表dp矩阵了,只是str1和str2一种对应关系,想象成一张表,这种对应关系是,要么斜线是连续递增,要么就是突然间变成0,可以用一个变量把这条线上所有的值都算出来。