关于倍增
学习博客
前几天\(lyk\)给我们讲了倍增但是\(emmmm\)他说话声音也太小了,坐在后排根本听不清楚诶,前边一群大佬还在叽叽喳喳的说话,上课效率低得一批。
\[\color{purple}{我太难了}\]
顾名思义倍增就是倍增,用\(dsr\)大佬的话来说就是\(wuwu\)腻。
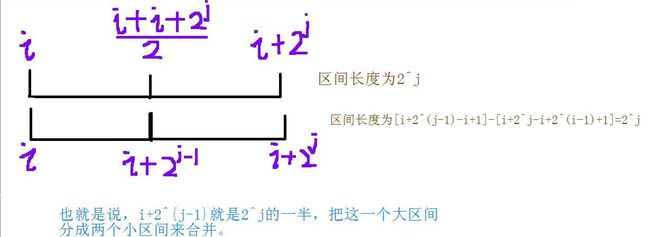
我们有一个数组\(f[i][j]\)表示从\(i\)开始的长度为\(2^j\)的区间即区间\([i,i+2^j]\)
递推公式:
预处理ST表
\(f[i][j]=max(f[i][j-1]),f[i+2^{j-1}][j-1]\)
说句闲话:
为什么这么写?我之前第一遍自己学的时候,看其他人的博客,有的直接不解释,有的说自己揣摩\(qwq\),我就是揣摩不出来才去看您的\(blog\)的哇。
后来\(lyk\)讲课问谁没听懂,偌大的教室里,只有我的小短手在教室后边高高的自信的举起,再不会就对不起\(lyk\)的一对一辅导了.
for(int i = 1; i <= m; i++) f[i][0] = read();//自己到自己这个区间
for(int j = 1; j <= log(m); j++)
for(int i = 1; i + (1 << j) <= m; i++)
f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]); j的循环范围
![]()
这里说一下为什么循环外层是\(j\)
再说一句闲话:
\(wtf\)?刚刚我在画图,阿龙过来来了一句:“你又待聂画画,打草纸组啥,光待聂画画。”嗯??你告诉我往草纸上画咋粘博客里。双面胶?来来来,舞台留给你,请开始你的表演。于是乎,\(lkx\)大佬帮我画了张图
回归正题,咱们看图说话并没有什么用的图假设我们先枚举\(i\)那么我们的枚举顺序就是\([1,1],[1,2]......[1,m]\)当我们更新到\([1,2]\)时,就要用到\([1,1]\)和\([2,2]\)这两个点,但是由于我们的外层循环是\(i\)此时的\([2,2]\)还没有值,所以这样更新出来的就是错的。
查询:
把我们需要查询的区间\([l,r]\)分成两段\([l,2^k]\)到\([r-2^k+1,r]\)其中这个\(k\)是\(2^k \leq r-l+1\)的所有数中的最大的数,就算这两部分互相覆盖由于他们是取最值,所以对答案没有影响
\(f[l][r]=max(f[l][k],f[r-(1<
为什么左端点是\(r-2^k+1\)可能只有我这样的才会问了好久才明白
简单一点我们设\(L\)为他的左端点,因为是一个闭区间且已知区间长度及区间右端点,可得方程\(r-L+1=2^k\)解得L即为左端点
倍增其实还有个很常用的应用:
求LCA!
此时设\(f[i][j]\)表示从节点\(i\)向上跳\(2^j\)个节点
\(f[i][j]=f[f[i][j-1]][j-1]\)
void work(int x, int fa) {
f[x][0] = fa;
dep[x] = dep[fa] + 1;
for(int i = 1; i < 20; i++)
f[x][i] = f[f[x][i - 1]][i - 1];
}
void dfs(int x, int fa) {
work(x, fa);
for(int i = head[x]; i; i = e[i].nxt)
if(e[i].to != fa) work(e[i].to, x);
}\(dfs\)的过程中更新
一种优化常数的方法:先处理出\(lg\)数组,表示以\(2\)为底\(i\)的对数
for(int i = 2; i <= n; i++)
lg[i] = lg[i >> 1] + 1;查询:
先使两个待查询的点跳到同一深度,然后再从\(i\)开始枚举,逼近他们的LCA,最后一定会是在他们的LCA的下一层,最后直接输出当前节点的爸爸也就是\(f[i][0]\)
if(dep[a] < dep[b]) swap(a, b);
for(int i = 20; i >= 0; i--)
if(dep[f[a][i]] >= dep[b])
a = f[a][i];//跳到同一深度
if(a == b) return a;//或者是b反正他俩都一样
for(int i = 20; i >= 0; i--)
if(f[a][i] != f[b][i])
a = f[a][i], b = f[b][i];//同时跳
return f[a][0];
}\(qwq\)貌似是有\(O(1)\)的的查询的喂
我:“\(lyk\),我\(O(1)\)查询的不会”
大佬:“\(hai \ xie\),不用会这锅啊,,谁写这\(hu\)滴啊”
路径最小权值
我们设\(w[i][j]\)表示从节点\(i\)向上跳\(2^j\)个节点内所经过的最小的权值
for(int j = 1; j < 20; j++)
for(int i = 1; i + (1 << j) - 1 <= tot; i++)
w[i][j] = min(w[i][j - 1], w[f[i][j - 1]][j - 1]);
//f[i][j]是预先处理处的代表i号点向上跳2^j步之后跳到的节点 历时一上午多点我总算把这篇文章磨完了........
谢谢收看, 祝身体健康!