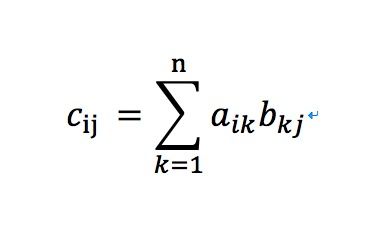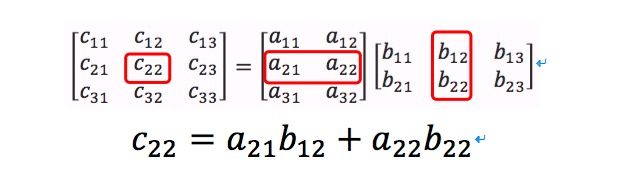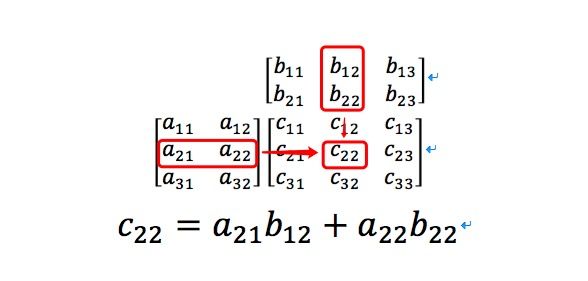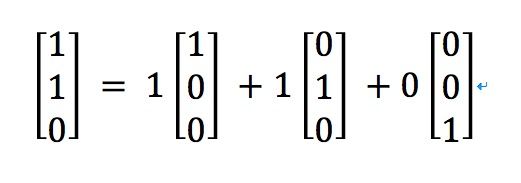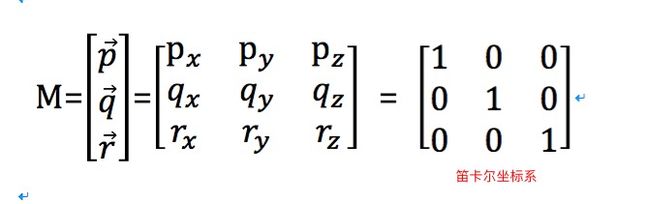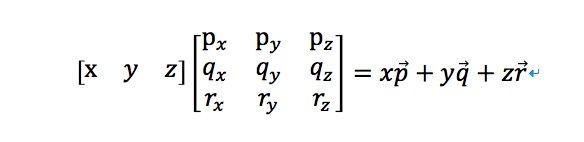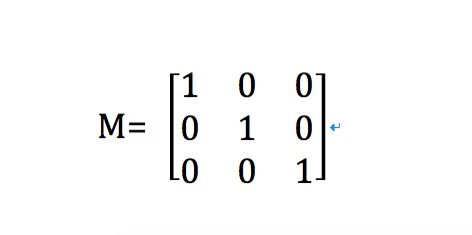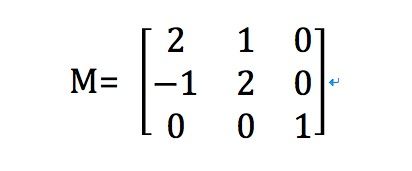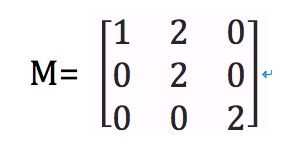矩阵的基本概念
矩阵其实就是向量的数组.向量算的上是特殊的一维矩阵.下面说一下几种特殊的方阵(行数和列数都相同的矩阵).
对角矩阵
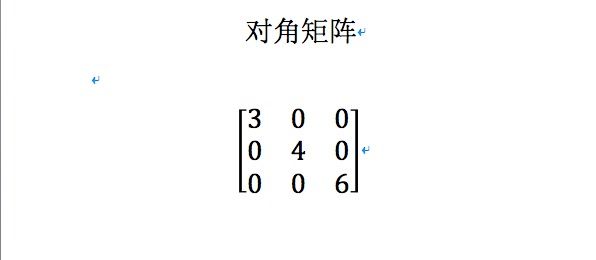
如果所有的飞对角线元素都为0,那么这样的矩阵称之为对角矩阵.
单位矩阵
单位矩阵是一种特殊的对角矩阵.n维单位矩阵记作In,是n x n的举证,对角线元素为1,其他元素为0.例如,3 x 3的矩阵如下所示.
(从书上抄袭过来的)单位矩阵非常的特殊,因为它是矩阵的乘法单位元.其基本性质是用任一个矩阵乘以单位矩阵,都将得到原矩阵.所有,从某种意义上讲,单位矩阵对矩阵的意义就如同1对标量的意义.
矩阵的运算
-
转置
矩阵的转置其实就沿着矩阵的对角线翻折.(当然了,下面给给出的方阵的转置,普通的a x b矩阵的转置矩阵为 b x a 矩阵)
矩阵转置的推理
- 将一个矩阵转置之后,再次转置一次,便会得到原来的矩阵.
- 对于任意的对角矩阵D,都有转置矩阵DT=D,包括单位矩阵I也是如此.
-
标量和矩阵的乘法
标量和矩阵的乘法只要将标量和矩阵中的每一个元素相乘即可.数学表达式如下所示.
-
矩阵的乘法(请深究❗️❗️❗️)
在某些情况下,两个矩阵是允许相乘.一个 r x n的矩阵A能够乘以一个n x c的矩阵B,结果是r x c的矩阵AB.
条件: 矩阵A的列数和矩阵B的行数必须一致.否则两个矩阵相乘是没有任何意义的.
矩阵的乘法计算如下: r x n的矩阵A能够乘以n x c的矩阵B,结果是r x c的矩阵C.C中任意元素Cij等于A的第i行向量与B的第j列向量的点乘结果.正式定义如下.
我们看一下具体的示例.比如c22的计算为[a21,a22]和[b12,b22]的点乘.
可能上面的表示还是不是太让人理解,下面我们就用一种更为简便的方式来说一下矩阵的乘法.我们把矩阵A拿到矩阵C的左边,把矩阵B拿到矩阵C的上面,并且使其对齐.这样看起来是不是更容易一些呢?
当然了,在集合中我们更多的是使用2x2和2x2的两个矩阵相乘,以及3x3和3x3的两个矩阵相乘.我们根据公式计算即可.
矩阵的几何解释
与其说矩阵的几何意义这么生涩难懂,不如说的是矩阵在几何中到底是有什么作用呢?一般来说,方阵可以描述任意的线性变换.,也就说,在几何当中,我们用矩阵表示几何体的空间变换.比如我们在程序中常用的平移、旋转、缩放等等.(没事,这时候说的可能很生涩,看到最后你就会明白怎么回事的)
为了更好的理解矩阵的几何意义,我们先用一个简单的示例来说明一下.如果我们把一张图片放入一个2D的坐标系中(为了给下面做铺垫,向量形式为[x,y,0]),并且规定它的大小为边长为1的正方形.向量p = [0,1,0],向量q = [1,0,0].如下图所示.
现在我们就单独的看图片的右上顶点 [1,1,0] (可看做向量).
首先我们先把[1,1,0]这个向量拆分一下.如下所示.
紧接着.我们要定义一下,p,q和r定义为指向 +x,+y,+z方面的单位向量.然后用单位向量表示图片的右上顶点 [1,1,0] .如下所示.
现在,向量[1,1,0]就被表示成p,q和r的线性变换了.向量p,q和r被称为基向量.这里的基向量是笛卡尔坐标系.但是事实上,一个坐标系能用任意的3个基向量表示.当然了,这三个向量不在同一个平面.向量p,q和r创建一个3x3的矩阵M.如下所示.
当然了,矩阵M可不单单只有上面的一种形式,上面的只能算是一种形式,记住我们说过的,一个坐标系能用任意的3个基向量表示.接下来,我们再次研究一个向量和一个矩阵相乘.(图形变换的开始部分),先看一下公式.
我们还是要借助一开始栋哥的那个坐标系图形.如果矩阵M如下所示.那么图形将不会发生任何变换.
接下来,我们就搞起图形变换了.如果矩阵M发生了如下改变,那么图形会有什么样的变化呢?
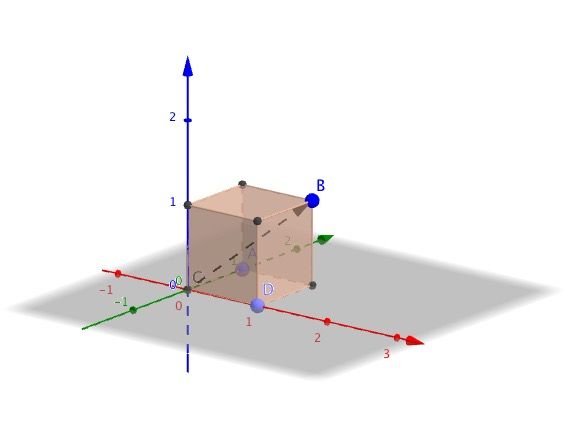
在矩阵M中.向量p从[1 0 0]变换到[2 1 0],q从[0 1 0]变换到[-1 2 0],r未发生变化.然后我们图形的右上点会再次发生缩放和旋转的变换.
得到效果图如下所示.
上面是2D中的变换,3D中的变化一样类似.例如现在有向量OB[1 1 1],如下图所示.
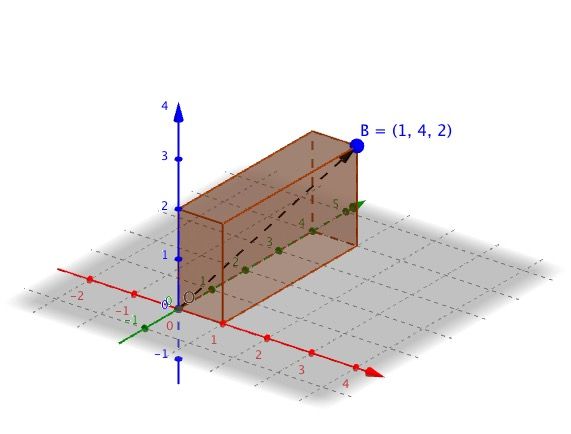
同时矩阵M如下所示.
结果变换之后,向量的图像如下所示.
图形变换的实质
看到上面我们已经对矩阵的基本使用有了了解.但是我们在实际的开发过程中遇到的图形变换的实质到底是什么呢?我个人感觉图形变换的实质就是变换图形自身的坐标系.通过变换基向量来使我们的图形发生改变.
最后还是要附上<<3D数学基础 图形与游戏开发>>的pdf版的传送门来结束矩阵的相关知识.