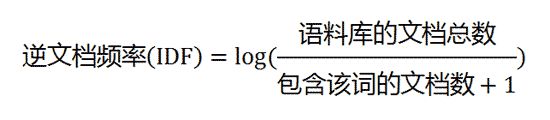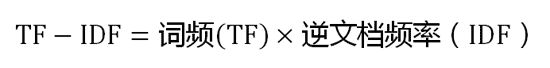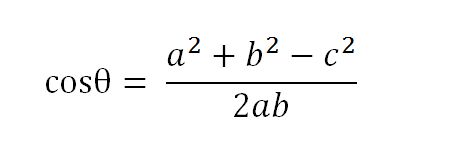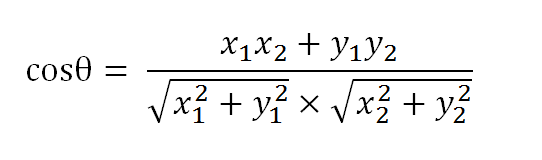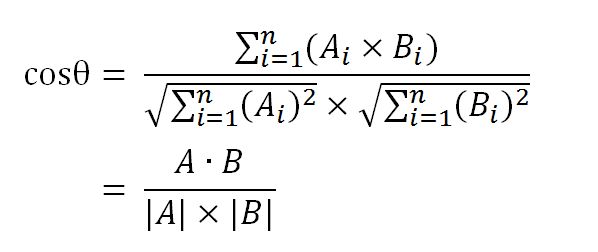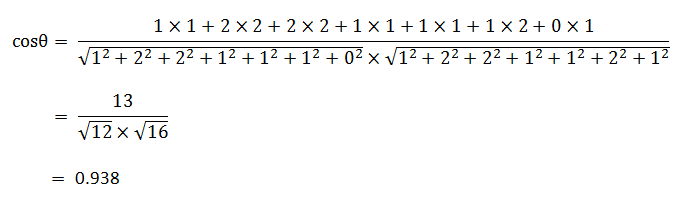1 TF-IDF算法
2 代码实现
3 余弦相似性
4 代码实现
1 TF-IDF算法
举个例子
假定现在有一篇长文《中国的蜜蜂养殖》,我们准备用计算机提取它的关键词。
一个容易想到的思路,就是找到出现次数最多的词。如果某个词很重要,它应该在这篇文章中多次出现。于是,我们进行"词频"(Term Frequency,缩写为TF)统计。
结果你肯定猜到了,出现次数最多的词是----"的"、"是"、"在"----这一类最常用的词。它们叫做"停用词"(stop words),表示对找到结果毫无帮助、必须过滤掉的词。
假设我们把它们都过滤掉了,只考虑剩下的有实际意义的词。这样又会遇到了另一个问题,我们可能发现"中国"、"蜜蜂"、"养殖"这三个词的出现次数一样多。这是不是意味着,作为关键词,它们的重要性是一样的?
显然不是这样。因为"中国"是很常见的词,相对而言,"蜜蜂"和"养殖"不那么常见。如果这三个词在一篇文章的出现次数一样多,有理由认为,"蜜蜂"和"养殖"的重要程度要大于"中国",也就是说,在关键词排序上面,"蜜蜂"和"养殖"应该排在"中国"的前面。
所以,我们需要一个重要性调整系数,衡量一个词是不是常见词。如果某个词比较少见,但是它在这篇文章中多次出现,那么它很可能就反映了这篇文章的特性,正是我们所需要的关键词。
用统计学语言表达,就是在词频的基础上,要对每个词分配一个"重要性"权重。最常见的词("的"、"是"、"在")给予最小的权重,较常见的词("中国")给予较小的权重,较少见的词("蜜蜂"、"养殖")给予较大的权重。这个权重叫做"逆文档频率"(Inverse Document Frequency,缩写为IDF),它的大小与一个词的常见程度成反比。
知道了"词频"(TF)和"逆文档频率"(IDF)以后,将这两个值相乘,就得到了一个词的TF-IDF值。某个词对文章的重要性越高,它的TF-IDF值就越大。所以,排在最前面的几个词,就是这篇文章的关键词。
下面就是这个算法的细节。
-
第一步,计算词频。
考虑到文章有长短之分,为了便于不同文章的比较,进行"词频"标准化。
或者
-
第二步,计算逆文档频率。
这时,需要一个语料库(corpus),用来模拟语言的使用环境。
如果一个词越常见,那么分母就越大,逆文档频率就越小越接近0。分母之所以要加1,是为了避免分母为0(即所有文档都不包含该词)。log表示对得到的值取对数。
-
第三步,计算TF-IDF。
可以看到,TF-IDF与一个词在文档中的出现次数成正比,与该词在整个语言中的出现次数成反比。所以,自动提取关键词的算法就很清楚了,就是计算出文档的每个词的TF-IDF值,然后按降序排列,取排在最前面的几个词。
TF-IDF算法的优点是简单快速,结果比较符合实际情况。缺点是,单纯以"词频"衡量一个词的重要性,不够全面,有时重要的词可能出现次数并不多。而且,这种算法无法体现词的位置信息,出现位置靠前的词与出现位置靠后的词,都被视为重要性相同,这是不正确的。
2 代码实现
实现思路:
- 通过中文分词器分词
- 统计词频
- 统计拟文档频率
- 计算结果,排序输出
通过中文分词器分词
/**
* 调用IKSegmenter切词,智能切词
* @param 读取的文本内容
* @return returnStr 切词结果,末尾加上""
* */
private static String segStr(String text) throws IOException{
String returnStr = "";
IKSegmenter ikSegmenter = new IKSegmenter(new StringReader(text), true);
Lexeme lexeme;
while ((lexeme = ikSegmenter.next()) != null) {
returnStr += lexeme.getLexemeText()+" ";
}
return returnStr;
}
统计词频TF
public static HashMap tf(String[] cutWordResult) {
HashMap tf = new HashMap();// 正规化
int wordNum = cutWordResult.length;
int wordtf = 0;
for (int i = 0; i < wordNum; i++) {
wordtf = 0;
for (int j = 0; j < wordNum; j++) {
if (cutWordResult[i] != " " && i != j) {
if (cutWordResult[i].equals(cutWordResult[j])) {
cutWordResult[j] = " ";
wordtf++;
}
}
}
if (cutWordResult[i] != " ") {
tf.put(cutWordResult[i], (new Double(++wordtf)) / wordNum);
cutWordResult[i] = " ";
}
}
return tf;
}
计算IDF
public static Map idf(String dir) throws FileNotFoundException, UnsupportedEncodingException,
IOException {
// 公式IDF=log((1+|D|)/|Dt|),其中|D|表示文档总数,|Dt|表示包含关键词t的文档数量。
Map idf = new HashMap();
List located = new ArrayList();
float Dt = 1;
float D = allTheNormalTF.size();// 文档总数
List key = fileList;// 存储各个文档名的List
Map> tfInIdf = allTheNormalTF;// 存储各个文档tf的Map
for (int i = 0; i < D; i++) {
HashMap temp = tfInIdf.get(key.get(i));
for (String word : temp.keySet()) {
Dt = 1;
if (!(located.contains(word))) {
for (int k = 0; k < D; k++) {
if (k != i) {
HashMap temp2 = tfInIdf.get(key.get(k));
if (temp2.keySet().contains(word)) {
located.add(word);
Dt = Dt + 1;
continue;
}
}
}
idf.put(word, (Double) Math.log((1.0 + D) / Dt));
}
}
}
return idf;
}
计算TF-IDF = TF*IDF
public static Map> tfidf(String RootURL_exSelectedWeb) throws IOException {
//Map singelFile = new TreeMap();
Map idf = TfIdf.idf(RootURL_exSelectedWeb);
Map> tf = TfIdf.tfOfAll(RootURL_exSelectedWeb);
Map> tfidf = new TreeMap>();;
for (String file : tf.keySet()) {//1 获取tf的键(文件名)
HashMap singelFile = tf.get(file);//2获取tf的值 (词语,词频)
for (String word : singelFile.keySet()) {//3 获取词语,通过词语遍历整个 文档词语,并逐一计算TF-IDF
singelFile.put(word, (idf.get(word)) * singelFile.get(word));
}
tfidf.put(file,singelFile);
}
return tfidf;
}
/**
* 将词频和文件名称联系起来
* @param dir
* @return allTheTf(文件名称,词语,正规化词频)
* @throws IOException
*/
public static Map> tfOfAll(String dir) throws IOException {
List fileList = TfIdf.readDirs(dir);
for (String file : fileList) {
HashMap dict = new HashMap();
dict = TfIdf.tf(TfIdf.cutWord(file));
allTheTf.put(file, dict);
}
return allTheTf;
}
3 余弦相似性
有些时候,除了找到关键词,我们还希望找到与原文章相似的其他文章。
为了找出相似的文章,需要用到"余弦相似性"(cosine similiarity)。下面,我举一个例子来说明,什么是"余弦相似性"。
为了简单起见,我们先从句子着手。
句子A:我喜欢看电视,不喜欢看电影。
句子B:我不喜欢看电视,也不喜欢看电影。
请问怎样才能计算上面两句话的相似程度?
基本思路是:如果这两句话的用词越相似,它们的内容就应该越相似。因此,可以从词频入手,计算它们的相似程度。
- 第一步,分词。
句子A:我/喜欢/看/电视,不/喜欢/看/电影。
句子B:我/不/喜欢/看/电视,也/不/喜欢/看/电影。
- 第二步,列出所有的词。
我,喜欢,看,电视,电影,不,也。
- 第三步,计算词频。
句子A:我 1,喜欢 2,看 2,电视 1,电影 1,不 1,也 0。
句子B:我 1,喜欢 2,看 2,电视 1,电影 1,不 2,也 1。
- 第四步,写出词频向量。
句子A:[1, 2, 2, 1, 1, 1, 0]
句子B:[1, 2, 2, 1, 1, 2, 1]
到这里,问题就变成了如何计算这两个向量的相似程度。
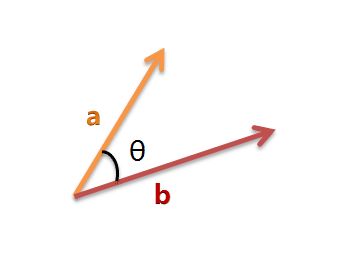
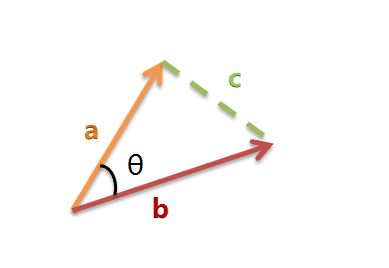
我们可以把它们想象成空间中的两条线段,都是从原点([0, 0, ...])出发,指向不同的方向。两条线段之间形成一个夹角,如果夹角为0度,意味着方向相同、线段重合;如果夹角为90度,意味着形成直角,方向完全不相似;如果夹角为180度,意味着方向正好相反。
因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
以二维空间为例,上图的a和b是两个向量,我们要计算它们的夹角θ。余弦定理告诉我们,可以用下面的公式求得:
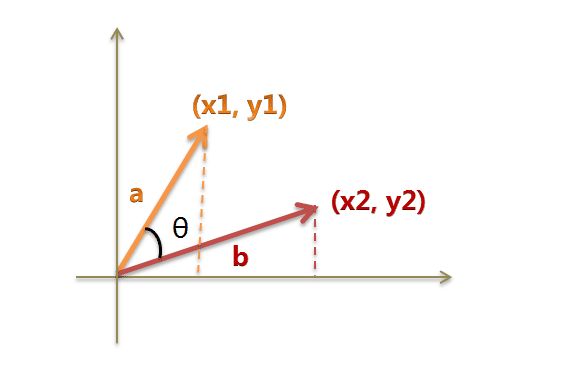
假定a向量是[x1, y1],b向量是[x2, y2],那么可以将余弦定理改写成下面的形式:
数学家已经证明,余弦的这种计算方法对n维向量也成立。假定A和B是两个n维向量,A是 [A1, A2, ..., An] ,B是 [B1, B2, ..., Bn] ,则A与B的夹角θ的余弦等于:
使用这个公式,我们就可以得到,句子A与句子B的夹角的余弦。
余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,这就叫"余弦相似性"。所以,上面的句子A和句子B是很相似的,事实上它们的夹角大约为20.3度。
由此,我们就得到了"找出相似文章"的一种算法:
(1)使用TF-IDF算法,找出两篇文章的关键词;
(2)每篇文章各取出若干个关键词(比如20个),合并成一个集合,计算每篇文章对于这个集合中的词的词频(为了避免文章长度的差异,可以使用相对词频);
(3)生成两篇文章各自的词频向量;
(4)计算两个向量的余弦相似度,值越大就表示越相似。
"余弦相似度"是一种非常有用的算法,只要是计算两个向量的相似程度,都可以采用它。
4 代码实现
private double computeSimTest_COS(Map testWordTFMap,
Map trainWordTFMap) {
double mul = 0, reslut=0, aMul=0, bMul=0,amulPow=0,bmulPow=0;
ArrayList aVector = new ArrayList();
ArrayList bVector = new ArrayList();
Set> testWordTFMapSet = testWordTFMap.entrySet();//除K文档外所有文档
Set> testTrainWordSet = trainWordTFMap.entrySet();//初始k文档
//分别遍历两个文本向量,取出其权值
for(Iterator> it = testWordTFMapSet.iterator(); it.hasNext();){
Map.Entry me = it.next();
aVector.add(me.getValue());
}
for(Iterator> it = testTrainWordSet.iterator(); it.hasNext();){
Map.Entry me = it.next();
bVector.add(me.getValue());
}
for(int i=0;i END