在前面两次的教程中,我们学习了方差分析和回归分析,它们都属于线性模型,即它们可以通过一系列连续型 和/或类别型预测变量来预测正态分布的响应变量。
但在许多情况下,假设因变量为正态分布(甚至连续型变量)并不合理,比如:结果变量可能是类别型的,如二值变量(比如:是/否、通过/未通过、活着/死亡)和多分类变量(比如差/良好/优秀)都显然不是正态分布;结果变量可能是计数型的(比如,一周交通事故的数目,每日酒水消耗的数量),这类变量都是非负的有限值,而且它们的均值和方差通常都是相关的(正态分布变量间不是如此,而是相互独立)。
广义线性模型就包含了非正态因变量的分析,本次教程的主要内容就是关于广义线性模型中流行的模型:Logistic回归(因变量为类别型)和泊松回归(因变量为计数型)。
开始本次的教程之前,同样的,我们默认大家已经了解了广义线性模型的统计学理论背景,直接进入R语言的函数学习。
温馨提示
1、本节内容重点内容较多, 务必紧跟红色标记。
2、测试数据及代码,关注科研猫公众号,后台回复:客服,联系客服领取
基础模型构建
R中可通过函数glm()(还可用其他专门的函数)拟合广义线性模型。它的形式与lm()类似,只是多了一些参数。函数的基本形式为
glm(formula, family=family(link=function), data=
其中参数formula和函数lm()中的用法类似,参数family则对应连接函数,不同的连接函数对应不同的回归模型。我们列出了概率分布(family)和相应默认的连接函数(function)。
因此可用如下代码拟合Logistic回归模型(可以左右滑动哦):
glm(Y~X1+X2+X3, family=binomial(link="logit"), data=mydata)
可用如下代码 拟合泊松回归模型:
glm(Y~X1+X2+X3, family=binomial(link="log"), data=mydata)
之前学习过的标注线性模型也可以用函数glm()拟合,如下代码的拟合结果相同。
glm(Y~X1+X2+X3, family=gaussian(link="identity"), data=mydata)
lm(Y~X1+X2+X3, data=mydata)
函数glm()和函数lm()的相同之处很多,与函数lm()连用的很多函数都可以和函数glm()连用,下表中展示了一部分和函数glm()连用的函数。
不管是标准线性模型还是正在讨论的广义线性模型,回归诊断都是不可或缺的。一般来说,前面标准线性模型中的诊断方法都可以用在广义线性模型的诊断中。这里有一些实用的建议:评价模型的适用性时,可以绘制初始响应变量的预测值与残差的图形、还可以列出帽子值(hat value)、学生化残差值和Cook距离统计量的近似值以及绘制这些统计量的参考图,当然你还可以找一些辅助函数,比如包car中的函数influencePlot()(这个函数会绘制一个综合的诊断图,帮助你判断模型适用性)。
其实上面的内容已经概括了R中广义线性模型拟合的主要过程,下面给出分别关于Logistic 回归和poisson回归的两个示例。
Logistic回归
以AER包中的数据框Affairs为例,我们将通过探究婚外情的数据来阐述Logistic 回归的过程。该数据从601 个参与者身上收集了9个变量,包括一年来婚外私通的频率以及参与者性别、年龄、婚龄、是否有小孩、宗教信仰程度(5分制,1分表示反对,5分表示非常信仰)、学历、职业(7种分类),还有对婚姻的自我评分(5分制,1表示非常不幸福,5表示非常幸福)。原数据中的婚外情(affairs)次数被记录下来,但是这里我们更关心二值型结果(有过一次婚外情/没有过婚外情),可以将affairs转化为二值型因子ynaffair,然后将ynaffair作为logistic回归的因变量。下面是把所有变量都加入模型中的拟合结果。
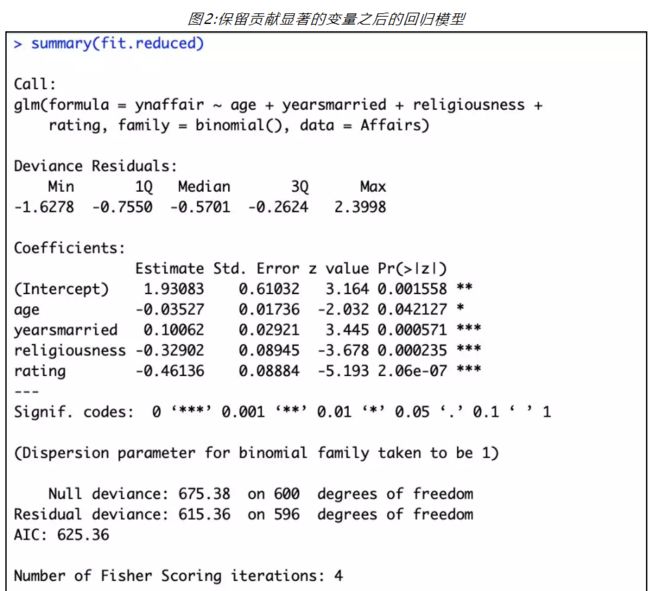
可以看到,图中只有age、yearsmarried、religiousness和rating对方程的贡献是显著的。因此只保留这四个变量再做一次回归分析。
去掉之后的拟合效果是否和之前有差异呢?用函数anova()对两个模型进行卡方检验,看到差异并不显著(p=0.2108),可以认为两个模型拟合程度一样好。
与标准线性模型不一样的是,在Logistic回归中,因变量是Y=1的对数优势比(log)。回归系数的含义是当其他预测变量不变时,一单位预测变量的变化可引起的因变量对数优势比的变化。在上面的例子中,yearsmarried的回归系数为0.10062,可以解释为yearsmarried增加一年,婚外情的优势比将乘以e0.10062=1.106(保持年龄、宗教信仰和婚姻评定不变),而如果增加10年,优势比将乘以1.10610,即2.7。如果这样还不够直观,还可以使用predict()函数,观察预测变量在各个水平时对结果概率的影响。图4中,当其他变量都取均值,随着yearsmarried的增加,出现婚外情的概率从0.136增加到0.260。
对于抽样于二项分布的样本而言,观测到的响应变量的方差大于期望的二项分布的方差(过度离势)时会导致奇异的标准误检验和不精确的显著性检验,此时需要将二项分布改为类二项分布(quasibinomial distribution)。检测过度离势的一种方法是比较二项分布模型的残差偏差与残差自由度,如果两者的比值比1大很多,便可认为存在过度离势。另一种方法是对过度离势进行检验(拟合模型两次,第一次使用family="binomial",第二次使用family="quasibinomial",然后对两个模型进行检验)。第二种方法的检验中最后的p值为0.340(代码已提供),显然不显著(p>0.05),这说明我们的模型不存在过度离势。
Logistic回归还有很多变种,比如:稳健logistic回归(robust包中的函数glmRob())、多项分布logistic回归(mlogit包中的函数mlogit())、序数logistic回归(rms包中的函数lrm()),它们的拟合过程都大同小异,但是评价模型优度和诊断更加复杂。
泊松回归
当通过一系列连续型和/或类别型预测变量来预测计数型结果变量时,泊松回归是一个非常有用的工具。示例将使用robust包中的 Breslow癫痫数据,响应变量为sumY(随机化后八周内癫痫发病数),预测变量为治疗条件(Trt)、年龄(Age)和前八周内的基础癫痫发病数(Base)(虽然整个数据集中有12个变量,但是我们只关注其中四个)。图5展示了一部分数据的分布特征。从图中可以清楚地看到因变量的偏倚特性以及可能的离群点。同时,药物治疗下癫痫发病数似乎变小了,且方差也变小了(泊松分布中,较小的方差伴随着较小的均值)。与标准最小二乘回归不同,泊松回归并不关注方差异质性。(事实上,所有的建模分析中,观察数据分布特点都是必不可少的步骤,在本次教程中的两个示例中我们都保留了这一步,而在实际的建模分析中需要按照数据分布特点来选择不同模型拟合数据,否则很容易事倍功半。)
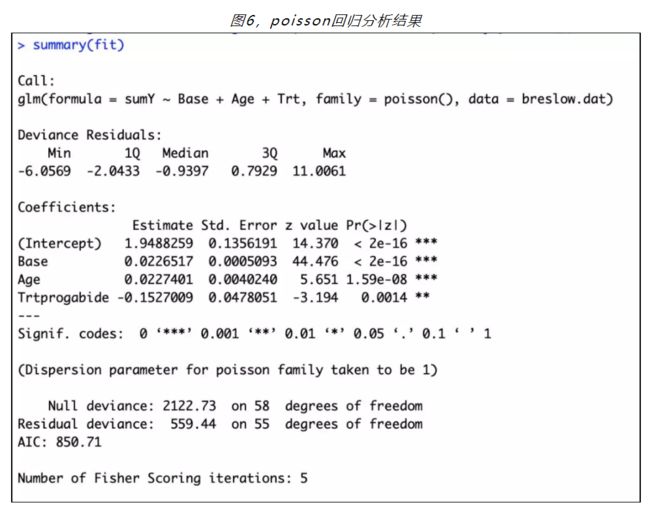
接下来进行回归分析。分析结果中,三个变量在p<0.05的情况下都非常显著。同时,变量Base、Age和Trt的三个回归系数分别为0.0227、0.0227和-0.1527。这说明保持其他变量不变,年龄增加一岁,期望的癫痫发病数将乘以e0.0227=1.023。这意味着年龄的增加与较高的癫痫发病数相关联。更为重要的是,一单位Trt的变化(即从安慰剂到治疗组),期望的癫痫发病数将乘以e-0.1527=0.86,也就是说,保持基础癫痫发病数和年龄不变,服药组相对于安慰剂组癫痫发病数降低了20%。
同样,还需要评价泊松模型的过度离势。泊松分布的方差和均值相等。当响应变量观测的方差比依据泊松分布预测的方差大时,泊松回归可能发生过度离势。处理计数型数据时经常发生过度离势,且过度离势会对结果的可解释性造成负面影响。与Logistic回归类似,此处如果残差偏差与残差自由度的比例远远大于1,那么表明存在过度离势。对于癫痫数据,它的比例为10.17(计算代码已提供,见文末客服二维码),远大于1。
在解决过度离势问题之前,推荐另一个检验poisson回归的过度离势的方法,即qcc包中的函数qcc.overdispersion.test(),这个函数的结果也说明这个回归模型确实存在过度离势的问题。通过用family="quasipoisson"替换family="poisson", 仍然可以使用glm()函数对该数据进行拟合。这与Logistic回归处理过度离势的方法是相同的。
图7中是修改参数之后的回归模型,所得的回归系数估计与泊松方法相同,但标准误变大了许多。此处,标准误越大将会导致Trt(和Age)的p值越大于0.05。当考虑过度离势,并控制基础癫痫数和年龄时,并没有充足的证据表明药物治疗相对于使用安慰剂能显著降低癫痫发病次数。
同样的poisson回归也有很多扩展的形式,如时间段变化的poisson回归(需要使用glm()函数中的offset选项)、零膨胀的泊松回归(pscl包中的函数zeroinfl()可做零膨胀泊松回归)、稳健泊松回归(robust包中的函数glmRob()可以拟合稳健广义线性模型,包含稳健泊松回归,当存在离群点和强影响点时,该方法会很有效。)。
小结&预告
到目前为止,R中基本统计分析就告一段落了,后面会介绍一些高级的数据挖掘分析,如主成分分析和聚类分析等等,在这些统计分析中,将看看处理潜变量的统计模型,即那些你坚信存在并能解释可观测变量的、无法被观测到的、 理论上的变量。具体而言,我们将学习如何使用因子分析方法检测和检验这些无法被观测到的变量的假设。
本期干货
·
- R语言回归分析 -
关注“科研猫”公众号,联系客服
胖雨小姐姐
or
折耳猫小姐姐
领取
R语言从入门到精通
经典系列课程
科研绘图
网络图
生存分析
GEO挖掘
功能富集
TCGA挖掘
更多科研新鲜资讯、文献精读和生物信息技能
请关注科研猫公众号
未经许可请勿随意转载,
版权事宜由上海辰明律师事务所提供法务支持