数据结构
数据结构分类(DataStructure)
- 数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
- 在任何问题中,数据元素之间不是孤立的,而是存在一定关系,这种关系称为结构(structure)。
根据数据元素之间关系的不同特性,可分为4种基本数据结构:
- 集合(set)集合中的数据元素除了存在“同属于一个集合”的关系外,不存在任何其他关系。
- 线性结构(linear structure)线性结构中数据元素存在着一对一的关系
- 树形结构(tree structure)树形结构中数据元素存在一对多的关系
- 图形结构(graphic structure)图形结构中数据元素存在多对多的关系
算法
- 算法可理解为基本运算及规定的运算顺序所构成的完整的解题步骤
- 算法可视为按照要求设计好的有限的确切的计算序列,并按步骤和序列解决某类问题。
数据结构和算法之间的关系
- 数据结构可认为是数据在程序中的存储结构和基本数据操作
- 算法是用来解决问题的,算法是基于数据结构的。
- 数据结构是问题的核心,是算法的基础。
算法的评价标准
- 运行时间(running time)
- 占用空间(storage space)有时需要牺牲空间换取时间,有时需要牺牲时间换取空间。
- 正确性(correctness)
- 可读性(readability)
- 健壮性(robustness)
线性表
线性表是线性结构的抽象(abstruct),其特点是结构中的数据元素之间存在一对一的线性关系,这种一对一的关系指的是数据元素之间的位置关系。
- 除第一个位置的数据元素外,其他数据元素位置的前面都只有一个数据元素。
- 除最后一个位置的数据元素外,其他数据元素的后面都只有一个元素。
也就是说,数据元素是一个接着一个排列的。因此,可把线性表现象成一种数据元素序列的数据结构。线性表就是位置有先后关系,一个接着一个排列的数据结构。
CLR中的线性表
C#1.1提供了一个非泛型接口IList接口,IList接口中的项是object,实现了IList接口的子类有
- ArrayList
- ListDictionary
- StringCollection
- StringDictionary
C#2.0提供了泛型的IList接口,实现IList接口的类有List。
List list = new List();
list.Add("alice");
list.Add("ben");
list.Add("carl");
Console.WriteLine(list[0]);//根据索引器访问元素
list.Remove("ben");
Console.WriteLine(list.Count);
list.Clear();
Console.WriteLine(list.Count);
Console.ReadKey();
实现线性表接口定义
namespace DataStructure
{
///
/// 线性表接口定义
///
///
{
///
/// 获取线性表长度,即元素个数。
///
///
/// 清空线性表
///
void Clear();
///
/// 判断线性表是否为空
///
///
/// 线性表插入元素
///
/// 数据项
/// 数据索引
void Insert(T item, int index);
///
/// 线性表追加元素
///
/// 数据项
void Append(T item);
///
/// 删除线性表元素
/// 根据索引删除指定位置的元素
///
/// 元素位置索引
///
/// 根据索引获取线性表元素
///
/// 元素索引
///
/// 索引器
/// 根据索引访问元素
///
/// 元素索引
///
/// 根据值获取索引值
///
/// 元素值
/// 线性表的实现方式
- 顺序表
- 单链表
- 双向链表
- 循环链表
顺序表
计算机内存中保存线性表最简单自然的方式,是把线性表中的元素一个接着一个放入顺序的存储单元中,这就是线性表的顺序存储(sequence storage)。
线性表的顺序存储指的是在内存中使用一块地址连续的空间依次存放线性表的数据元素,使用这种方式存放的线性表叫做顺序表(sequence list)。
顺序表的特点是表中相邻的数据元素在内存中存储的位置是相邻的。
顺序表的任意存储
假设:顺序表中每个数据元素占用 w 个存储单元,设第 i 个数据元素的存储地址为 Loc(ai),则有
Loc(ai) = Loc(a1) + (i-1)*w
1<= i <= n式中的Loc(ai) 表示第1个数据元素 a1 的存储地址,也就是顺序表的起始存储地址,成为顺序表的基地址(base address)。
也就是说,只要知道顺序表的基地址和每个数据元素所占的存储单元的个数,就可以求出顺序表中任意一个数据元素的存储地址。
由于计算顺序表中每个数据元素存储地址的时间是相同的,所以顺序表具有任意存取的特定,即可以在任意位置存取数据。
C#中的数组在内存中占用的存储空间是一组连续的存储区域。因此,数组具有任意存取的特点。所以,数组天生具有表示顺序表的数据存储区域的特性。
namespace DataStructure
{
///
/// 顺序表
///
/// : IList
{
///
/// 用于存取数据的数组
///
private T[] data;
///
/// 用于记录存取元素的个数
///
private int count = 0;
///
/// 自定义构造器
/// 不提供自动扩容
///
/// 元素最大个数
public SequenceList(int maxsize)
{
data = new T[maxsize];
count = 0;
}
///
/// 默认构造器
/// 默认容量为10
///
public SequenceList():this(10)
{
}
///
/// 索引器
///
///
///
/// 追加元素
///
///
public void Append(T item)
{
//判断数组是否饱和
if(count == data.Length)
{
System.Console.WriteLine("当前顺序表已存满,禁止存入数据。");
}
else
{
data[count] = item;
count++;
}
//todo:返回当前数组的索引
}
///
/// 清空数据
///
public void Clear()
{
count = 0;
}
///
/// 获取数据个数
///
/// 数据个数
public int Count()
{
return count;
}
///
/// 根据索引删除元素
///
///
public T Delete(int index)
{
T item = data[index];
//把数据向前移动
for(int i = index+1;i
/// 根据索引获取值
///
///
///
/// 插入元素
///
///
///
public void Insert(T item, int index)
{
//从后向前
for(int i = count - 1; i >= index; i--)
{
data[i + 1] = data[i];
}
data[index] = item;
count++;
}
///
/// 判断是否为空
///
///
/// 根据值获取索引
///
///
/// 顺序表是用地址连续的存储单元顺序存储线性表中的各个数据元素,逻辑上相邻的数据元素在物理位置上也是相邻的。
- 优点:在顺序表中查找任何一个位置上的数据元素快速高效,这是顺序存储的优点。
- 缺点:在对顺序表进行插入和删除时,需通过移动数据元素来实现,影响运行效率。
- 特点:存取快,插入删除慢。
链表
线性表的另一种存储结构 - 链式存储(LinkedStorage),这种线性表叫做链表(LinkedList)。
链表不要求逻辑上相邻的数据元素在物理存储位置上也相邻
- 优点:在对链表进行插入和删除时无需移动数据元素
- 缺点:链表因此失去了顺序表可随机存储的优势
- 特点:插入删除较快,查找较慢。
链表节点
链表是用一组任意的存储单元来存储线性表中的数据元素,这组存储单元可以是连续,有可以不是连续的。那么,如何表示两个数据元素逻辑上是相邻的关系呢?也就是说,如何表示数据元素之间的线性关系呢?
为此,在存储数据元素时,除了存储数据本身的元信息外,还要存储与它相邻的数据元素的存储地址。这两部分信息组成该数据元素的存储映像(image),称之为节点(node)。
我们把存储数据元素本身的域称为节点的数据域(data domain),把存储与之相邻的数据元素的存储地址信息的域称为节点的引用域(reference domain)。
因此,线性表通过每个节点的引用域形成了一根“链条”,这就是链表名称的由来。
namespace DataStructure
{
///
/// 链表节点
///
///
{
///
/// 存储的数据
///
private T data;
///
/// 指针
/// 用于指向下一个元素
///
private Node next;
///
/// 默认构造器
///
public Node()
{
data = default(T);
next = null;
}
public Node(T value)
{
data = value;
next = null;
}
public Node(Node next)
{
this.next = next;
}
public Node(T value, Node next)
{
this.data = value;
this.next = next;
}
///
/// 数据 存取器
///
public T Data
{
get { return data; }
set { data = value; }
}
///
/// 指针 存取器
///
public Node Next
{
get { return next; }
set { next = value; }
}
}
}
单链表
顺序表是用地址连续的存储单元顺序存储线性表中的各个元素,逻辑上相邻你的数据元素在物理位置上也相邻。因此,在线性表中查找任何一个位置上的数据元素非常方便,这是顺序表存储的优点。但是,在对顺序表进行插入和删除时,需要通过移动数据元素来实现,影响了运行效率。
线性表的另一种存储结构-链式存储(Linked Storage),这样的线性表叫链表(Linked List)。链表不要求逻辑的数据元素在物理存储位置上也相邻。因此,在对链表进行插入和删除时,无需移动数据元素,但同时也失去了顺序表可随机存储的优点。
namespace DataStructure
{
class SingleLinkedList : IList
{
///
/// 头节点
///
private Node head;
///
/// 构造器
///
public SingleLinkedList()
{
head = null;
}
///
/// 索引器
///
///
/// node = head;
//获取当前节点
for (int i = 0; i <= index; i++)
{
node = node.Next;
}
return node.Data;
}
}
///
/// 单链表添加新节点
///
///
public void Append(T item)
{
//创建新节点
Node node = new Node(item);
//判断头节点
if(head == null)
{
head = node;
}
else
{
//追加至尾节点
Node tmp = head;
//获取尾节点
while (true)
{
if (tmp.Next != null)
{
tmp = tmp.Next;
}
else
{
break;
}
}
//将新节点放入链表尾部
tmp.Next = node;
}
}
///
/// 清空单链表
///
public void Clear()
{
head = null;
}
///
/// 获取单链表长度
///
/// tmp = head;
while (true)
{
//若当前节点存在下一个节点则长度自增1
if (tmp.Next != null)
{
count++;
tmp = tmp.Next;
}
else
{
break;
}
}
return count;
}
///
/// 根据索引删除单链表元素
///
///
/// tmp = head;
//获取当前节点的上一个节点
for(int i=1; i<=index - 1; i++)
{
tmp = tmp.Next;
}
Node prevNode = tmp;
//获取当前节点的数据
Node currNode = tmp.Next;
data = currNode.Data;
//获取当前节点的下一个节点
Node nextNode = tmp.Next.Next;
//删除当前节点
prevNode.Next = nextNode;
}
return data;
}
///
/// 根据指定索引获取单链表数据
///
///
///
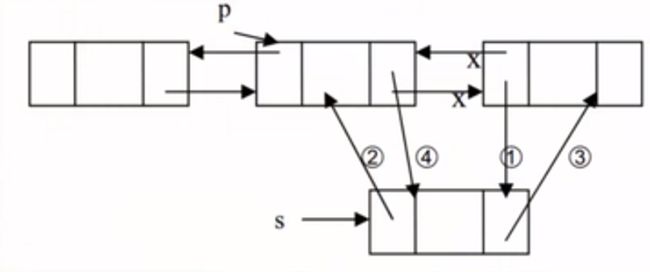
/// 指定位置插入新节点
///
///
///
public void Insert(T item, int index)
{
//目标节点
Node node = new Node(item);
//插入位置为头节点
if(index == 0)
{
node.Next = head;
head = node;
}
else
{
//目标节点的上一个节点
Node tmp = head;
//临时节点后移index-1个位置
for (int i=1; i<=index - 1; i++)
{
tmp = tmp.Next;
}
Node prevNode = tmp;
//获取目标节点
Node currNode = tmp.Next;
//插入新节点
prevNode.Next = node;
node.Next = currNode;
}
}
///
/// 判断单链表是否为空
///
///
/// 根据数据获取单链表的索引
///
///
/// tmp = head;
if(tmp == null)
{
return -1;
}
else
{
int index = 0;
while (true)
{
if (tmp.Data.Equals(value))
{
return index;
}
else
{
if(tmp.Next != null)
{
tmp = tmp.Next;
}
else
{
break;
}
}
index++;
}
return -1;
}
}
}
}
双向链表
单链表允许从一个结点直接访问它的后继节点,所以,查找后继结点的时间复杂度是O(1)。但是,要查找某个结点的直接前驱结点,只能从表的头引用开始遍历各个结点。
如果某个结点的Next等于该结点,那么,这个结点就是该结点的直接前驱结点。也就是说,查找直接前驱结点的时间复杂度是O(n),n是单链表的长度。当然,我们也可以在结点的引用域内保存直接前驱结点的地址而非直接后继节点的地址。这样,查找直接前驱结点的时间复杂度只有O(1),但查找后继节点的时间复杂度是O(n)。
如果希望查找直接前驱结点和直接后继节点的时间复杂度都是O(1),那么,需要在结点中设置两个引用域,一个保存直接前驱结点的地址叫做prev,一个直接后继节点的地址叫做next,这样的链表就是双向链表Doubly Linked List。
循环链表
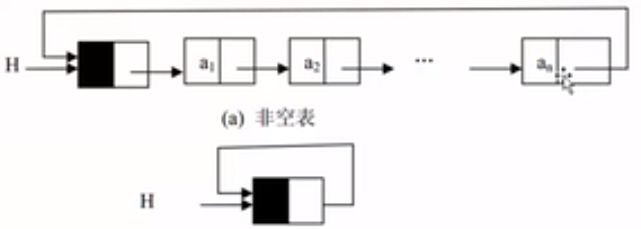
某些应用不需要链表中有明显的头尾结点,在这种情况下,可能需要方便地从最后一个节点访问到第一个节点。此时,最后一个节点的引用域不是空引用,而是保存第一个结点的地址,如果该链表带结点则保存的是头结点的地址,也就是头引用的值。
带头结点的循环链表(Circular Linked List)
栈和队列
栈和队列是非常重要的两种数据结构,在软件设计中应用很多。栈和队列也是线性结构,线性表、栈、队列这三种数据结构的数据元素以及数据元素间的逻辑关系完全相同。差别在于线性表的操作不受限制,而栈和队列的操作受到限制。栈的操作只能在表的一端进行,队列的插入操作在表的一端进行而且其它操作在表的另一端进行。所以,把栈和队列称为操作受限的线性表。
栈
栈(stack)是操作限定在表的尾端进行的线性表,表尾由于要进行插入、删除等操作。所以,它具有特殊的含义,把表尾称为栈顶(Top),另一端是固定的,叫做栈底(Bottom)。当栈中没有数据元素时叫做空栈(Empty Stack)。
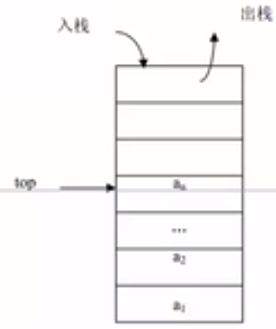
栈通常标记为:S = (a1, a2,... an),S是英文单词Stack的第一个字母。a1为栈底元素,an为栈顶元素。这n个数据元素按照a1, a2...an的顺序依次入栈,而出栈的次序相反。an第一个出栈,a1最后一个出栈。所以,栈的操作是按照后进先出(LIFO, Last In First Out)或先进后出(FILO, First In Last Out)的原则进行的。因此,栈又称为LIFO表或FILO表。
栈的操作示意图