笔者刚开始接触数据挖掘,入门参考书籍为Peter Harrington编著的《机器学习》,文章代码亦大量借鉴于书中。
信息增益
导入模块:
from math import log
import operator
计算给定数据集的香农熵:
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
lableCounts = {}
for featVec in dataSet:
currentLable = featVec[-1]
if currentLable not in lableCounts.keys():
lableCounts[currentLable] = 0
lableCounts[currentLable] += 1
shannonEnt = 0
for key in lableCounts:
prob = float(lableCounts[key])/numEntries
shannonEnt -= prob * log(prob,2)
return shannonEnt
创建简单的数据集:
def createDataSet():
dataSet = [[1,1,0,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],[0,0,1,'run'],[0,1,0,'fight'],[0,1,1,'run']]
lables = ['weapon','bullet','blood']
return dataSet,lables
字段说明
[1,1,0,'fight']
| 数值 | 武器类型 | 子弹 | 血量 |
|---|---|---|---|
| 0 | 步枪 | 少 | 少 |
| 1 | 机枪 | 多 | 多 |
| 值 | 行为类别 |
|---|---|
| fight | 战斗 |
| run | 逃跑 |
按行打印数据集
def printData(myData):
for item in myData:
print '%s' %(item)
用Python命令提示符输入下列命令:
>>> import tree
>>> myDat,lable = tree.createDataSet()
>>> tree.printData(myDat)
[1, 1, 0, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[0, 0, 1, 'run']
[0, 1, 0, 'fight']
[0, 1, 1, 'run']
>>> tree.calcShannonEnt(myDat)
0.863120568566631
得到香农熵为0.863120568566631
熵越高,则混合的数据也越多。
为数据集添加新分类surrender:
>>> myDat[0][-1] = 'surrender'
>>> tree.printData(myDat)
[1, 1, 0, 'surrender']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[0, 0, 1, 'run']
[0, 1, 0, 'fight']
[0, 1, 1, 'run']
>>> tree.calcShannonEnt(myDat)
1.3787834934861756
得到香农熵为1.3787834934861756
划分数据集
按照给定特征划分数据集:
def splitDataSet(dataSet,axis,value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
输入Python命令,分别提取武器类型为1(机枪)和0(步枪)的行为:
>>> reload(tree)
>>> myDat,lable = tree.createDataSet()
>>> tree.printData(myDat)
[1, 1, 0, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[0, 0, 1, 'run']
[0, 1, 0, 'fight']
[0, 1, 1, 'run']
>>> tree.splitDataSet(myDat,0,1)
[[1, 0, 'fight'], [0, 1, 'fight'], [0, 1, 'fight'], [0, 1, 'fight']]
>>> tree.splitDataSet(myDat,0,0)
[[0, 1, 'run'], [1, 0, 'fight'], [1, 1, 'run']]
选择最好的数据集划分方式:
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
chooseBestFeatureToSplit调用的数据需要满足的要求:
- 数据必须是一种由列表元素组成的列表
- 所有列表元素都要具有相同的数据长度
- 数据的最后一列是当前数据的类别标签
在开始划分数据集之前,先计算整个数据集的原始香农熵,保存最初的无序度量值,用于与划分完之后的数据集计算的熵值进行比较,从而计算信息增益。
遍历当前特征中的所有唯一属性值,对每个特征划分一次数据集,然后计算数据集的新熵值,并对所有唯一特征值得到的熵求和。
最后,比较所有特征中的信息增益,返回最好特征划分的索引值。
>>> reload(tree)
>>> myDat,lable = tree.createDataSet()
>>> tree.printData(myDat)
[1, 1, 0, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[0, 0, 1, 'run']
[0, 1, 0, 'fight']
[0, 1, 1, 'run']
>>> tree.chooseBestFeatureToSplit(myDat)
0.469565211115
0.00597771142377
0.16958442967
0
在划分数据集之前之后信息发生的变化称为信息增益。
| 特征 | 信息增益 |
|---|---|
| 武器类型 | 0.469565211115 |
| 子弹数量 | 0.00597771142377 |
| 血量 | 0.16958442967 |
运行结果告诉我们,第0个特征,也就是武器类型是最好的用于划分数据集的特征。
递归构建决策树
创建的函数代码:
def createTree(dataSet,lables):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLable = lables[bestFeat]
myTree = {bestFeatLable:{}}
del(lables[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLables = lables[:]
myTree[bestFeatLable][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLables)
return myTree
递归结束的条件:
- 遍历完所有划分数据集的属性
- 每个分支下的素有实力都有相同的分类
所有的类标签完全相同,则返回该类标签。如果使用完了所有特征,仍然不能将数据集划分成仅包含唯一类别的分组,则通过majorityCnt挑选出出现次数最多的类别标签作为返回值。
选出出现次数最多的分类名称:
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(),key = operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
为测试代码的实际输出结果,在Python命令提示符中输入下列命令:
>>> reload(tree)
>>> myDat,lable = tree.createDataSet()
>>> tree.printData(myDat)
[1, 1, 0, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[1, 0, 1, 'fight']
[0, 0, 1, 'run']
[0, 1, 0, 'fight']
[0, 1, 1, 'run']
>>> tree.createTree(myDat,lable)
0.469565211115
0.00597771142377
0.16958442967
0.251629167388
0.918295834054
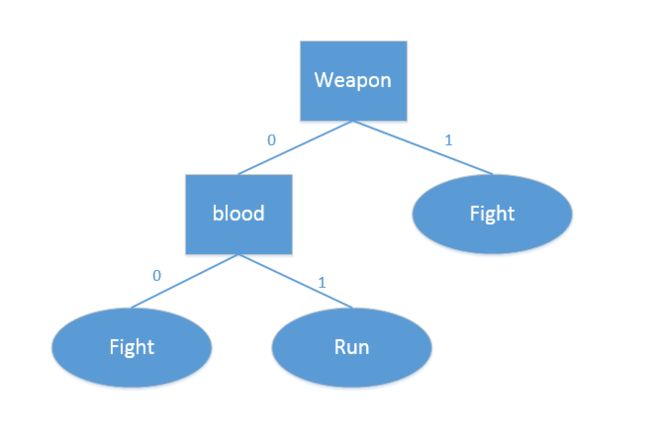
{'weapon': {0: {'blood': {0: 'fight', 1: 'run'}}, 1: 'fight'}}
createTree返回的嵌套字典包含了很多代表树结构的信息,从左边开始,第一个关键字weapon是第一个划分数据集的特征名称,该关键字的值也是另一个数据字典。第二个关键字是weapon特征划分的数据集,这些关键字的值是weapon节点的子节点。这些值可能是类标签,也可能是另一个数据字典。如果值是类标签,则该节点是叶子节点;如果值是另一个数据字典,则子节点是一个判断节点,这种格式结构不断重复就构成了整棵。该例子中包含了3个叶子节点和2个判断节点。