标签(空格分隔): 算法 C++ 笔试
第三题:
描述
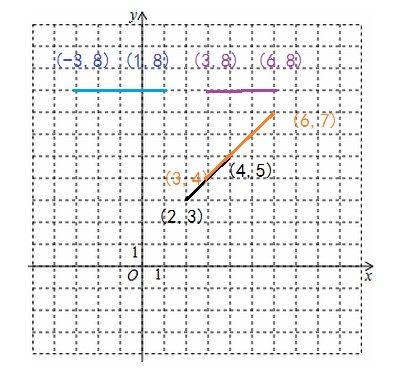
小王最近在开发一种新的游戏引擎,但是最近遇到了性能瓶颈。于是他打算从最基本的画线功能开始分析优化。画线其实就是调用一次drawline命令,根据给出的两端坐标,在屏幕画出对应的线段。但是小王发现,很多的drawline其实可以合并在一起,譬如下图中的线段(2,3)-(4,5)和线段(3,4)-(6,7),其实可以合并为一次drawline命令,直接画出线段(2,3)-(6,7)。当然有些线段是无法合并的,如线段(-3,8)-(1,8)和线段(3,8)-(6,8),就必须调用两次drawline命令。
画线示意图。注意颜色只是用于区分,实际线段都是黑色
给出N条drawline指令以及对应的线段坐标,小王想知道,实际最少用多少次drawline指令就可以画出来。
小王想先从最简单的情况开始分析优化,所以线段只包含四种情况:水平线段,垂直线段以及正反45度的线段。
输入
每个输入数据包含多个测试点。
第一行为测试点的个数 S ≤ 10。之后是 S 个测试点的数据。
每个测试点的第一行为 N(N ≤ 105)。之后是 N 行,每行包含4个整数:x0, y0, x1, y1,表示线段(x0,y0)-(x1,y1),坐标的范围在[-108, 108],保证线段的长度大于0。
输出
对于每个测试点,对应的结果输出一行,表示最少用多少次指令即可完成所有的画线。
样例输入
2
4
3 8 6 8
-3 8 1 8
2 3 4 5
3 4 6 7
5
1 1 2 2
2 2 3 3
3 3 4 2
4 2 5 1
1 0 100 0
样例输出
3
3
#include
#include
#include
#include
using namespace std::tr1;
using namespace std;
bool gongyueshu(vector vec, vector vec2,float xie){
if(abs(vec[0]-vec2[2])==0&&xie!=-1) return false;
else if(abs(vec[0]-vec2[2])==0&&xie==-1){
if((vec[1]-vec2[3])<=((vec[1]-vec[3])+(vec2[1]-vec2[3]))) return true;
else return false;
}
else if(abs(vec[0]-vec2[2])!=0){
float duijiao = fabs(float(vec[1]-vec2[3]))/fabs(float(vec[0]-vec2[2]));
if(duijiao-xie>0.01) return false;
int len1 = abs(vec[3]-vec[1]);
int len2 = abs(vec[2]-vec[0]);
int len3 = abs(vec2[3]-vec2[1]);
int len4 = abs(vec2[2]-vec2[0]);
int len5=0,len6=0;
if(vec[0] v1,vector v2){
return v1[0]> vec){
for(int i=0;i>>& map_){
unordered_map>> ::iterator it;
for(it=map_.begin();it!=map_.end();++it){
sort(it->second.begin(),it->second.end(),less_); //需要对整体进行排序
}
}
int test(unordered_map>> map_){
int result=0;
unordered_map>> ::iterator it;
for(it=map_.begin();it!=map_.end();++it){
vector> vec = it->second;
if(vec.size()==1) ++result;
else{
++result;
for(int j = 0;jfirst));
else ++result;
}
}
}
return result;
}
int main(){
int num=0;
cin>>num;
while(num){
unordered_map>> map_;
int row=0;
cin>>row;
while(row){
vector vec;
int tmp;
for(int j =0;j<4;j++){
cin>>tmp;
vec.push_back(tmp);
}
if(vec[2]-vec[0]==0) map_[-1].push_back(vec);
else{
float xl = (vec[3]-vec[1])/(vec[2]-vec[0]); //将同一个斜率的线放在一起。
map_[xl].push_back(vec);
}
row--;
}
num--;
sort_map(map_);
cout << endl<> 4
*/
第二题:“源代码编译” 描述
在网易游戏的日常工作中,C++ 是一门常用的语言。面对众多的 C++ 代码,等待源文件编译的漫长时间是个令人糟心的时刻,一直以来大家对此怨声载道。终于有一天,大家找到了你,一位优秀的程序员,请你来帮忙分析一下编译速度的瓶颈。
经过一番调查和研究,你发现一些源代码之间是有依赖关系的。例如,某个源文件 a.cpp 编译链接生成了动态链接库 a.dll,而 b.cpp 编译链接生成的 b.dll 依赖于 a.dll。这个时候,必须等待 a.dll 生成之后才能生成 b.dll。为了表达简单,我们这个时候称 b.cpp 依赖于 a.cpp。
网易游戏内部使用了一个分布式并行的编译平台,可以同时编译多个不互相依赖的文件,大大提高了源代码的编译速度。然而当某些依赖链很长的时候,这个编译平台也无能为力,只能按照依赖顺序一个一个完成编译,从而造成了很长的编译时间。
为了验证这个想法,你决定着手通过代码分析这些文件之间的编译顺序。已知这些文件的文件名,以及这些文件所依赖的其他文件,你需要编写一个程序,输出一个可行的编译所有源文件的编译顺序。如果有多种可行的序列,请输出所有文件名序列中字典序最小的那一个(序列 (a1, a2, ..., an) 字典序小于序列 (b1, b2, ..., bn),当且仅当存在某个 i ,使得 ai 的字典序小于 bi,并且对于任意 j < i ,都有 aj = bj)。
输入
输入包含多组测试数据。
输入的第一行包含一个整数 T(T ≤ 100),表示输入中一共包含有 T 组测试数据。
每组测试数据第一行是一个整数 N(N ≤ 1000),表示一共有 N 个源代码文件。随后一共有 N 行数据,其中第 i(0 ≤ i < N) 行数据包含序号为 i 的源代码文件的依赖信息。每一行开头是一个字符串,表示这一个文件的文件名,随后一个整数 m(0 ≤ m ≤ N),表示编译这个源文件之前需要先编译 m 个依赖文件。之后是 m 个整数 j0 ... jm-1,表示这 m 个依赖文件的序号(0 ≤ j < N) 。所有的文件名仅由小写字母、数字或“.”组成,并且不会超过 10 个字符。保证 n 个源代码文件的文件名互不相同。
输出
对于每一组输入,按照编译先后顺序输出一组可行的编译顺序,一行一个文件名。如果有多种可行的序列,请输出所有文件名序列中字典序最小的那一个。如果不存在可行的编译顺序,输出一行 ERROR。每组测试数据末尾输出一个空行。
样例输入
3
2
a.cpp 0
b.cpp 1 0
2
cb 0
c 0
2
a.cpp 1 1
b.cpp 1 0
样例输出
a.cpp
b.cpp
c
cb
ERROR
这里用到的其实只是普通的拓扑排序
#include
#include
#include
#include
//#include
#include 第一道题的暴力解法:
#include
#include #include
#include
#include
using namespace std;
int long_vector(string str ,int i){
int res=0;
int j=1;
while(i-j>=0&&i+jres){
res = long_vector(str,i);
}
}
return res+1;
}
bool check(string s){
for(int i=0;i>row;
while(row>0){
string str="";
string res="";
cin>>str;
int lens = long_string_(str,res);
if(lens==str.size()) cout<< lens+1;
else cout<< lens+find_best(res);
row--;
}
return 0;
}
找回文子串如果是这么找就一定会超时:
#include
#include
#include
using namespace std;
int long_vector(string str ,int i){
int res=0;
int j=1;
while(i-j>=0&&i+jres){
res = long_vector(str,i);
}
}
return res;
}
int main(){
int row=0;
cin>>row;
while(row>0){
string str="";
cin>>str;
cout<< find_best(str);
row--;
}
return 0;
}
后缀数组如何解决最长回文子串:
如下目标字符串:bananas 其长度为7,则后缀数组的长度为7,分别是以b开头的子串(长度为7),以a开头的子串(长度为6),以n开头的子串(长度为5)....最后一个是以s开头的子串(长度为1)。
最朴素的算法是,让后缀数组之间两两比较,找出最长的公共子串(注意,这里的最长的公共子串必须是以首字符参与匹配的,如果首字母都不匹配,那么长度为0,比如,后缀[0]和后缀1之间的首字母不匹配,则两者的最长公共子串长度为0.),但是时间复杂度为O(n^2)。
后缀数组的应用:
例1:最长公共前缀
(给定一个字符串,询问某两个后缀的最长公共前缀)
这道题好像最好的方法是用到后缀树
后缀是指从某个位置i开始到整个串末尾结束的一个特殊子串。字符串r的从第i个字符开始的后缀表示为Suffix(i),也就是Suffix(i) = r[i...len(r)]。
后缀数组(SA[i]存放排名第i大的子串首字符下标)
后缀数组 SA 是一个一维数组,它保存1...n 的某个排列 SA1,SA2,......,SA[n],并且保证Suffix(SA[i])< Suffix(SA[i+1]), 1<=i< n. 也就是将S 的n个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA中。
后缀数组举例:
如下目标字符串:bananas 其长度为7,则后缀数组的长度为7,分别是以b开头的子串(长度为7),以a开头的子串(长度为6),以n开头的子串(长度为5)....最后一个是以s开头的子串(长度为1)。
名次数组 Rank[i] 保存的是 Suffix(i) 在所有后缀中从小到大排列的“名次”。
关于字符串大小的比较:关于字符串的大小比较,是指通常所说的“字典顺序”比较,也就是对于两个字符串u、v,令i从1开始顺次比较u[i]和v[i],如果u[i]=v[i]则令i加1,否则若u[i]
从字符串的大小比较定义来看,S的开头两个位置后缀u和v进行比较的结果不可能是相等,因为u==v的必要条件len(u)=len(v) 是不可能满足的。
对于约定的字符串S,从位置i开头的后缀直接写成Suffix(i),省去参数S。
倍增法构造后缀数组
最直接的方法,当然是把S的后缀都看作是一些普通的字符串,按照一般字符串排序的方法对它们从小到大进行排序。 不难看出这样的方法是很笨拙的,因为它没有利用各个后缀之间的有机联系,所以它的效率不高。倍增算法正式充分利用了各个后缀之间的联系,将构造后缀数组的数组的最坏时间复杂度成功降到了O(nlogn);
注:这个是排序的关键字~
算法目标:
求得串的sa数组和rank数组
易知sa和rank互为逆操作,即sa[rank[i]] = i; Rank[sa[i]] = i;(所以我们只要求得其一,就能O(n) 算出另一个)
注:这个结论只在最后完成排序的时候符合。
但sa和rank的定义一直都是适用的。
原因是最后的时候不会存在相同(rank相等)的两个子串。
算法基本流程
- 设排序的当前长度是h。Suffix(i,h)
- 先按H=1,对suffix(i,H)(0
说到回文子串的几种方法:
暴力方法,求出每一个子串,之后判断是不是回文,找到最长的那个。
求每一个子串时间复杂度O(N2),判断子串是不是回文O(N),两者是相乘关系,所以时间复杂度为O(N3)。
string findLongestPalindrome(string &s)
{
int length=s.size();//字符串长度
int maxlength=0;//最长回文字符串长度
int start;//最长回文字符串起始地址
for(int i=0;i=tmp2&&j-i>maxlength)
{
maxlength=j-i+1;
start=i;
}
}
if(maxlength>0)
return s.substr(start,maxlength);//求子串
return NULL;
}
动态规划
回文字符串的子串也是回文,比如P[i,j](表示以i开始以j结束的子串)是回文字符串,那么P[i+1,j-1]也是回文字符串。这样最长回文子串就能分解成一系列子问题了。这样需要额外的空间O(N2),算法复杂度也是O(N2)。
首先定义状态方程和转移方程:
P[i,j]=0表示子串[i,j]不是回文串。P[i,j]=1表示子串[i,j]是回文串。P[i,i]=1。
P[i,j] =P[i+1,j-1],if(s[i]==s[j])
P[i,j] =0,if(s[i]!=s[j])
string findLongestPalindrome(string &s)
{
const int length=s.size();
int maxlength=0;
int start;
bool P[50][50]={false};
for(int i=0;i=2)
return s.substr(start,maxlength);
return NULL;
}
中心扩展
中心扩展就是把给定的字符串的每一个字母当做中心,向两边扩展,这样来找最长的子回文串。算法复杂度为O(N^2)。
但是要考虑两种情况:
1、像aba,这样长度为奇数。
2、想abba,这样长度为偶数。
string findLongestPalindrome(string &s)
{
const int length=s.size();
int maxlength=0;
int start;
for(int i=0;i=0&&kmaxlength)
{
maxlength=k-j+1;
start=j;
}
j--;
k++;
}
}
for(int i=0;i=0&&kmaxlength)
{
maxlength=k-j+1;
start=j;
}
j--;
k++;
}
}
if(maxlength>0)
return s.substr(start,maxlength);
return NULL;
}
4、Manacher法 》》算法介绍
Manacher法只能解决例如aba这样长度为奇数的回文串,对于abba这样的不能解决,于是就在里面添加特殊字符。我是添加了“#”,使abba变为a#b#b#a。这个算法就是利用已有回文串的对称性来计算的,具体算法复杂度为O(N),我没看出来,因为有两个嵌套的for循环。
具体原理参考这里。
测试代码中我没过滤掉“#”。
#define min(x, y) ((x)<(y)?(x):(y))
#define max(x, y) ((x)<(y)?(y):(x))
string findLongestPalindrome3(string s)
{
int length=s.size();
for(int i=0,k=1;i=0&&i+jmax)
{
max=rad[i];
center=i;
}
}
return s.substr(center-max,2*max+1);
}
字符串处理题目:
输入
输入包括多行。每行是一个字符串,长度不超过200。
一行的末尾与下一行的开头没有关系。
输出
输出包含多行,为输入按照描述中变换的结果。
样例输入
The Marshtomp has seen it all before.
marshTomp is beaten by fjxmlhx!
AmarshtompB
样例输出
The fjxmlhx has seen it all before.
fjxmlhx is beaten by fjxmlhx!
AfjxmlhxB
#include
#include
#include
#include
#include
using namespace std;
void deal_str(string str_lower){
for(int i=0;i 01背包(复习下动态规划法)
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为两个正整数N和M,表示奖品的个数,以及小Ho手中的奖券数。
接下来的n行描述每一行描述一个奖品,其中第i行为两个整数need(i)和value(i),意义如前文所述。
测试数据保证
对于100%的数据,N的值不超过500,M的值不超过10^5
对于100%的数据,need(i)不超过2*10^5, value(i)不超过10^3
输出
对于每组测试数据,输出一个整数Ans,表示小Ho可以获得的总喜好值。
样例输入
5 1000
144 990
487 436
210 673
567 58
1056 897
样例输出
2099
#include
#include
#include
using namespace std;
vector c; //重量
vector v; //价值
vector> result; //表
///f()函数,计算在i+1个物品和重量上限j的条件下的最大背包价值
int f(int i,int j) //第i个物品,重量上限j //0号物品即第一个物品
{
if (i == 0&&c[i]<=j) //0号物品且重量小于上限
{
return v[i]; //把0号物品放入背包,背包价值为第0号物品的价值
}
if (i == 0 && c[i] > j) //0号物品且重量大于上限
{
return 0; //物品放不进背包,此时背包为空,背包价值为0
}
//不是0号物品的情况
if (i != 0 && j-c[i] >= 0) //i号物品可以放入背包
{
//判断放入和不放入两种情况下背包的价值,选择价值大的方案
return (result[i - 1][j - c[i]] + v[i]) > result[i - 1][j] ? (result[i - 1][j - c[i]] + v[i]) : result[i - 1][j];
} //把这个物品放入背包 //不放入背包
else //i号物品不可以放入背包
return result[i - 1][j];
}
int getResult(int top, int num)
{
if (num == 0) //有0个物品
return 0;
else
{
for (int i = 0; i < num; i++) //第i个物品
{
for (int j = 0; j <= top; j++) //重量 我觉得会超时的地方在于这个重量!!,如果重量很大
{
result[i][j] = f(i,j);
//建表,result[i][j]表示有0,1,2...i个物品和j的重量限制下的最大背包价值
}
}
return result[num-1][top];
}
}
int main()
{
int num; //物品数量
int top; //背包容量
scanf("%d",&num);
scanf("%d",&top);
for (int i = 0; i < num; i++) //第i个物品的重量和价值
{
vector row(top+1,0);
result.push_back(row);
int need=0,value=0;
scanf("%d",&need);
scanf("%d",&value);
c.push_back(need);
v.push_back(value);
}
cout << getResult(top, num) << endl;
return 0;
}
最长回文子串 AC的解法:
#include
#include
int Min(int a, int b)
{
if (a < b)
return a;
return b;
}
int LPS(std::string &s)
{
std::string new_s="";
int s_len = s.length();
new_s.resize(2 * s_len + 3);
int new_s_len = new_s.length();
new_s[0] = '$';
new_s[1] = '#';
new_s[new_s_len - 1] = '@';
for (int i = 0,j=2; i < s_len; ++i)
{
new_s[j++] = s[i];
new_s[j++] = '#';
}
int *p = new int[new_s_len + 1];
int id = 0;//记录已经查找过的边界最靠右回文串的中心
int maxLPS = 1;
p[0] = 1;
for (int i = 1; i < new_s_len-1; ++i)
{
if (p[id] + id - 1 >= i)//有交集的情况
p[i] = Min(p[2 * id - i], p[id] + id - i);
else//无交集的情况
p[i] = 1;
while (new_s[i - p[i]] == new_s[i + p[i]])//确定能伸展多少,上面if的情况是不会执行这个循环的
++p[i];
if (p[id] + id < p[i] + i)//重新确定伸展最右的回文子串中心
id = i;
if (p[i]>maxLPS)//保存当前最长回文子串的长度(还要-1)
maxLPS = p[i];
}
delete[] p;
return maxLPS - 1;
}
int main()
{
int N;
std::string s;
std::cin >> N;
while (N--)
{
std::cin >> s;
std::cout< 在无序地情况下进行二分查找(用快排进行实现,但是快排有个最大的问题,就是如果是在有序地情况下会退化成冒泡排序,所以这个地方的种子数据,就需要选的相对随机一点)
输入
第1行:2个整数N,K。N表示数组长度,K表示需要查找的数;
第2行:N个整数,表示a[1..N],保证不会出现重复的数,1≤a[i]≤2,000,000,000。 (注意,这里2000000000< 2147483647 所以用Int 型就可以了,4个字节可以表示的数也是很大的。)
输出
第1行:一个整数t,表示K在数组中是第t小的数,若K不在数组中,输出-1。
样例输入
10 5180
2970 663 5480 4192 4949 1 1387 4428 5180 2761
样例输出
9
#include
#include
#include
#include
using namespace std;
int my_find(vector &nums,int target,int left_,int right_){
int left=left_,right=right_;
if(left==right&&nums[left]!=target) return -1;
swap(nums[left],nums[(left+right)/2]);
int cur = nums[left];
while(left=cur) right--;
if(leftcur) return my_find(nums,target,left+1,right_);
}
int main(){
int row=0,target=0;
vector nums;
scanf("%d",&row);
scanf("%d",&target);
int num=0;
while(row>0){
scanf("%d",&num);
nums.push_back(num);
row--;
}
cout< 二分查找之第第K小的数,以及二分查找之第k大的数的标准做法
#include
#include
#include
#include
using namespace std;
int my_find(vector &nums,int target,int left_,int right_){
int left=left_,right=right_;
if(left==right&&left!=target) return -1;
swap(nums[left],nums[(left+right)/2]);
int cur = nums[left];
while(left=cur) right--;
if(leftleft) return my_find(nums,target,left+1,right_);
}
int main(){
int row=0,target=0;
vector nums;
scanf("%d%d",&row,&target);
int num=0;
while(row>0){
scanf("%d",&num);
nums.push_back(num);
row--;
}
cout< tip:
对于字符串,用find函数去寻找指定的内容的话,如果能找到了,就是返回下标,如果没有找到,就是返回s.npos
网易游戏编程题
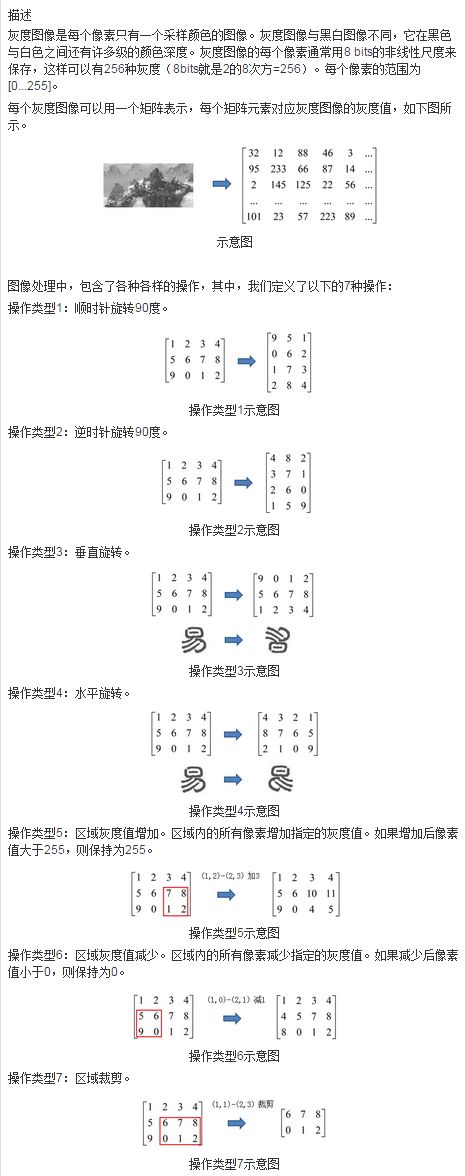
第一题:图像处理
输入
每个输入数据包含多个测试点。
输入数据的第一行为S(S <= 10),表示测试数据有S个测试点。
测试点的第一行为N, M (1 <= N, M <= 100),表示矩阵的大小。之后N行,每行包含M个数字,表示对应的像素值,数字的范围在[0...255]。
之后一行是数T(1 <= T <= 50)。之后T行,每行表示一个操作。每行的第一个数表示操作类型。
其中,对于操作类型5和6,该行还会包括5个数x0, y0, x1, y1, value(0 < value <= 255)。分别表示区域左上角(x0, y0)以及区域右下角(x1, y1),该区域中所有像素值增加/减少value。对于操作类型7,该行还会包括4个数x0, y0, x1, y1,表示裁剪的区域左上角(x0, y0)和区域右下角(x1, y1)。
保证所有操作均合法,操作中指定的区域一定是矩阵中的合法区域。保证最后的矩形一定非空。
输出
对应每个测试点输出一行,包括四个数字,分别表示最后矩阵的大小,左上角(0, 0)的像素大小,以及所有像素值的总和。
样例输入
2
3 4
1 2 3 4
5 6 7 8
9 0 1 2
3
1
7 1 0 3 1
5 1 0 1 1 5
2 2
7 8
7 2
1
1
样例输出
3 2 0 34
2 2 7 24
我的答案:
#include
#include
#include
#include
using namespace std;
vector> case1(vector>& vec){
int m= vec.size();
int n= vec[0].size();
vector> new_vec(n,vector(m));
for(int i=0;i> case2(vector>& vec){
int m= vec.size();
int n= vec[0].size();
vector> new_vec(n,vector(m));
for(int i=0;i> case3(vector>& vec){
int m= vec.size();
int n= vec[0].size();
vector> new_vec(m,vector(n));
for(int i=0;i> case4(vector>& vec){
int m= vec.size();
int n= vec[0].size();
vector> new_vec(m,vector(n));
for(int i=0;i>& vec,int x0,int y0,int x1,int y1,int value){
int m= vec.size();
int n= vec[0].size();
for(int i=x0;i<=x1;i++)
for(int j=y0;j<=y1;j++){
vec[i][j]+=value;
if(vec[i][j]>255) vec[i][j]=255;
}
}
void case6(vector>& vec,int x0,int y0,int x1,int y1,int value){
int m= vec.size();
int n= vec[0].size();
for(int i=x0;i<=x1;i++)
for(int j=y0;j<=y1;j++){
vec[i][j]-=value;
if(vec[i][j]<0) vec[i][j]=0;
}
}
vector> case7(vector>& vec,int x0,int y0,int x1,int y1){
int m= vec.size();
int n= vec[0].size();
int m1 = x1-x0+1;
int n1 = y1-y0+1;
vector> new_vec(m1,vector(n1));
for(int i=x0;i<=x1;i++)
for(int j=y0;j<=y1;j++){
new_vec[i-x0][j-y0] = vec[i][j];
}
return new_vec;
}
void res(vector> vec){
int m= vec.size();
int n= vec[0].size();
int val = vec[0][0];
int res_=0;
for(int i=0;i0){
scanf("%d",&m);
scanf("%d",&n);
vector> vec(m,vector(n));
for(int i=0;i 一起消消毒
(这道题用bool表进行维护是正确的,因为通过bool表,可以相互不会干扰,方便进行统一赋值)
#include
#include
#include
#include
using namespace std;
bool v[25][25];
char k[25][25];
int n,m,s,xa,ya,xb,yb;
int adjust()
{
int count,p,ret=0;
memset(v,0,sizeof(v));
for(int i=0;i=3){
for(int p=j-count;p=3){
for(int p=m-count;p=3){
for(int p=i-count;p=3){
for(int p=n-count;p=0;i--){
if(k[i][j]!='.'){
k[p][j]=k[i][j];
p--;
}
}
for(;p>=0;p--){
k[p][j]='.';
}
}
return ret;
}
int main()
{
int sum,r;
scanf("%d",&s);
while(s--)
{
sum=0;
//矩阵的初始化
memset(k,0,sizeof(k));
scanf("%d%d",&n,&m);
for(int i=0;i 题目3 : 神奇的数
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
Celin一直认为万物皆数,他总会花上很多的时间去研究和数相关的一些问题。最近他在研究一种神奇的数,这种数包含以下3个特征:
(1) 这个数至少包含('2', '3', '5')中的任意一个数字;
(2) 这个数不能出现'18';
(3) 这个数能被7整除。
如217,280,1393,9520均为同时满足三个条件的神奇的数。
而140,798不符合条件(1),518,1183不符合条件(2),12,1727不符合条件(3),这些数均不是Celin要找的神奇的数。
给出一个范围[N, M],Celin想知道在范围内(包括N和M两个边界在内)一共有多少个符合条件的神奇的数。
输入
每个输入数据包含多个测试点。
第一行为测试点的个数S <= 100,然后是S个测试点的数据。
每个测试点为一行数据,该行包含两个数N, M (1 <= N <= M <= 1018),表示范围。
hihoCoder平台的长整形为long long。数据范围较大,请注意优化您的算法。
输出
对应每个测试点的结果输出一行,表示范围内总共有多少个神奇的数。
样例输入
3
1 100
200 210
1000 1005
样例输出
6
2
0
思路:三个条件相对独立,每个条件单独的都有数位DP的例题,所以这里的处理方式是针对不同的条件设置了不同的状态空间,每个条件的判定相对容易。
#include
#include
#include
using namespace std;
int dp[20][2][2][7];
int digit[20];
long long dfs(int len,bool state, int has, int sum, bool fp)
{
if(!len)
{
if(has == 1 && sum == 0)
{
return 1;
}
else return 0;
}
if(!fp && dp[len][state][has][sum] != -1)
{
return dp[len][state][has][sum];
}
long long ret = 0 , fpmax = fp ? digit[len] : 9;
for(int i = 0; i <= fpmax; i++)
{
// 不含18
if(state && i == 8)
continue;
//含有2,3,5
int prehas = has;
int presum = sum;
sum *= 10;
sum += i;
sum %= 7;
if(!has && (i == 2 || i == 3 || i == 5))
{
has = 1;
}
ret += dfs(len - 1,i == 1, has, sum, fp && i == fpmax);
has = prehas;
sum = presum;
}
if(!fp)
{
dp[len][state][has][sum] = ret;
}
return ret;
}
long long f(long long n)
{
long long len = 0;
while(n)
{
digit[++len] = n % 10;
n /= 10;
}
return dfs(len,false, 0, 0, true);
}
int main()
{
long long a,b;
memset(dp, -1, sizeof(dp));
while(scanf("%lld %lld", &a, &b) != EOF)
{
printf("%lld\n", f(b) - f(a - 1));
}
return 0;
}
网易游戏有面试一个其他的题目:
A:给你一亿个数字,然后找出两个唯一相同的数字出来:
(首先一亿的数字,占400M内存,内存应该是够的)
因为相比来说,异或是处理速度比哈希的处理速度要快,所以,不妨把所有的数字先异或一遍,这样就能够得到不含相同的数字的异或结果;然后再将每一个数字与该数字进行一次异或,保存在一个unordered_map里,这样查找速度是1,时间复杂度是O(N),空间复杂度为800M
B:(这道题其实有几个变种,第一个变种,就是数字范围在1到1000,然后给你1001个数字,求出里面的重复的数字是多少)
这种其实就是通过异或即可。