深度学习不仅仅在擅长于从现有数据中发现规律,而且它能主动运用规律创造出现实世界没有的实例来。例如给网络输入大量的人脸图片,让它识别人脸特征,然后我们可以指导网络创建出现实世界中不存在的人脸图像,把深度学习应用在创造性生成上是当前AI领域非常热门的应用。
从本节开始,我们将接触神经网络在图像生成方面的应用。有两种专门构建的网络在图像生成上能实现良好效果,一种网络叫变分编解码器,另一种叫生成型对抗性网络。这两种网络不仅仅能有与图片生成,还能用于音乐,声音,以及文本生成,但是在图像生成的效果上表现最好,因此接下来我们看看如何构建相应网络实现生成功能。
图像生成的关键思想是,使用网络构造一个向量空间,空间中每一个向量都可以映射成一张真实图片。在网络中有一个模块,读入该向量后,能够经过一系列运算把向量转换成一张图片所对应的二维向量,这个模块在编解码器网络里称为解码器。
编解码器网络的运行流畅如下:
首先我们把大量图片输入到网络中,网络识别图片并抽取图片中蕴含的规律,它把这些规律进行编码,以向量的形式存储,向量的长度越大,它就能存储越多的图片信息。接着网络的解码器模块解读编码向量,由于向量存储的是所有图片共同展现的人脸特征,而不是某个具体人的人脸特征,因此解码器解读编码向量后,就能根据向量蕴含的人脸特征进行绘图,最终构造出原来训练图片里没有的人脸图案,但这个人脸图案的特征与训练图片里面的人脸特征有相关性。
其实我们在前面章节已经接触过特征向量。在前面讲解单词向量时,所谓的单词向量就是一种特征向量。向量空间中,某个方向,也就是向量里面的某些分量可能记录了训练数据的某一方面的特征,对应人脸图片来说,向量可能有一部分分量用来记录笑容特征,某些分量可能记录了眼睛特征,某些分量可能记录了头发特征,所有这些特征综合起来就可能形成一张人脸。由于解码器能够识别向量中不同分量代表的信息,因此它把向量拆分解读之后,再按照向量分量表达的信息来绘制像素点,最终就可以完成一张人脸图片的绘制。
编解码器网络发明与2013和2014年,它能够把高维数据所展现的特征编码成低维向量,然后再把低维向量转换为原来数据所表示的高维向量。但这种还原并非原封不动的还原,而是把低维向量编码的信息展现出来。编解码网络有点像压缩和解压,把解码器模块把输入数据转变成另一种数据量较小的数据格式,而解码器再把该数据格式还原成输入数据,然而编解码器网络可不是简单的进行数据压缩和解压。
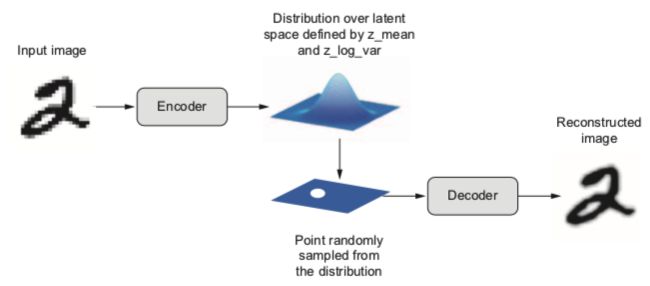
如上图,编解码器网络本质上是在学习输入图片像素点的统计信息,知道了像素点在统计上的分布规律后,它再按照相应的分布规律产生像素点,于是产生的图片与输入图片很像,但因为是根据统计规律随机产生的,因此生成的图片会产生某些变异。当我们把大量图片输入网络进行学习时,网络的编码器统计图片像素点变化的均值和方差,以及变化特征,这些特征编码成中间向量格式,然后解码器读取该向量,用随机方法把还原图片像素点的变化规律。
接下来我们看看代码的实现:
from keras.models import Model
from keras import layers
import numpy as np
import keras
#输入图片为28*28的灰度图
img_shape = (28, 28, 1)
batch_size = 16
#将输入图片编码为只含有2个分量的向量
latent_dim = 2
input_img = keras.Input(shape = img_shape)
#设计编码器部分
x = layers.Conv2D(32, 3, padding = 'same', activation = 'relu')(input_img)
x = layers.Conv2D(64, 3, padding = 'same', activation = 'relu', strides = (2,2))(x)
x = layers.Conv2D(64, 3, padding = 'same', activation = 'relu')(x)
x = layers.Conv2D(64, 3, padding = 'same', activation = 'relu')(x)
shape = K.int_shape(x)
#把x压扁成一维向量
x = layers.Flatten()(x)
x = layers.Dense(32, activation = 'relu')(x)
#统计输入图片像素点统计规律上的均值
z_mean = layers.Dense(latent_dim)(x)
#统计输入图片像素点统计规律上的方差
z_log_var = layers.Dense(latent_dim)(x)
'''
均值和方差决定了像素点的变化规律,在统计上发现,大量的事物在数据上的变化都遵守正太分布,一旦掌握
了其数值变化的方差和均值,我们就掌握了它变化的规律。在实现解码器时,我们也认为输入图片的像素点
同样符合正太分布,下面函数根据上面得到的均值和方差构造正太分布,然后从这个分布中进行抽样构成要
还原图片的像素点
'''
def sampling(args):
z_mean, z_log_var = args
#构造一个随机值,然后使用它到给定正太分布中生成一个结果,这类似于丢一个骰子然后看点数
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean = 0, stddev = 1.)
return z_mean + K.exp(z_log_var) * epsilon
z = layers.Lambda(sampling)([z_mean, z_log_var])
上面是编码器的实现,从这里我们看到,深度学习其本质并没有什么神奇的魔力,它本质是对大量的输入数据进行数理统计,由此就能掌握事物的变化规律。我们再看看解码器的实现:
#解码过程是对编码过程的逆运算
decoder_input = layers.Input(K.int_shape(z)[1:])
x = layers.Dense(np.prod(shape[1:]), activation = 'relu')(decoder_input)
#恢复为向量压扁前的格式
x = layers.Reshape(shape[1:])(x)
#对编码器的卷积运输进行逆操作
x = layers.Conv2DTranspose(32, 3, padding = 'same', activation = 'relu',
strides = (2, 2))(x)
x = layers.Conv2D(1, 3, padding = 'same', activation = 'sigmoid')(x)
decoder = Model(decoder_input, x)
z_decoded = decoder(z)
接下来我们设置网络的损失函数:
'''
我们定义网络的损失框架没有提供,因此我们自己动手写
'''
class CustomVariationLayer(keras.layers.Layer):
def vae_loss(self, x, z_decoded):
x = K.flatten(x)
z_decoded = K.flatten(z_decoded)
#计算生成二维数组与输入图片二维数组对应元素的差方和
xent_loss = keras.metrics.binary_crossentropy(x, z_decoded)
#计算网络生成像素点统计分布与输入图片像素点变化分布的差异
k1_loss = -5e-4 * K.mean(
1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis = -1
)
return K.mean(xent_loss + k1_loss)
def call(self, inputs):
x = inputs[0]
z_decoded = inputs[1]
loss = self.vae_loss(x, z_decoded)
self.add_loss(loss, inputs = inputs)
return x
y = CustomVariationLayer()([input_img, z_decoded])
损失函数要计算两部分,一部分是网络解码得到的二维数组与输入图片二维数组对应元素的差方和,第二是网络构造的二维数组,其元素变化规律与输入图片元素变化规律在统计上的差异,也就是我们希望网络生成的二维数组,其元素变化在统计上的均值与方差和输入图片像素点在统计上的均值和方差要尽可能的小。这里涉及到数理统计方面的知识,不了解可以直接忽略掉。
最后我们看看网络的训练过程:
from keras.datasets import mnist
vae = Model(input_img, y)
vae.compile(optimizer = 'rmsprop', loss = None)
vae.summary()
(x_train, _), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_train = x_train.reshape(x_train.shape + (1,))
x_test = x_test.astype('float32') / 255.
x_test = x_test.reshape(x_test.shape + (1,))
vae.fit(x = x_train, y = None,
shuffle = True,
epochs = 10,
batch_size = batch_size,
validation_data = (x_test, None))
训练后,我们看看网络对输入图片的还原效果:
import matplotlib.pyp
lot as plt
from scipy.stats import norm
#一次呈现15*15个数字
n = 15
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]])
z_sample = np.tile(z_sample, batch_size).reshape(batch_size, 2)
x_decoded = decoder.predict(z_sample, batch_size = batch_size)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i+1) * digit_size,
j * digit_size: (j+1) * digit_size] = digit
plt.figure(figsize = (10, 10))
plt.imshow(figure, cmap = 'Greys_r')
plt.show()
上面代码运行后可以看到,网络学习了数字图片中像素点的分布规律后,按照规律构造还原会相应的数字图片,还原的图片与输入图片大致相同,但在细节上有些许差异:
本节的内容比较抽象,不好理解。因为它用到了很多数学知识,没有深厚的数学功底你很难掌握本节内容,这也是现在程序员很难转行到人工智能,特别是深度学习领域的根本原因,因为他们具备的是工程思维,而人工智能要求你具备深厚的数学基础以及科学研究思维,如果你理解不了本节内容不要紧,只要把代码敲一遍,看看结果,具有一个感性认识也就可以了。
更详细的讲解和代码调试演示过程,请点击链接
更多技术信息,包括操作系统,编译器,面试算法,机器学习,人工智能,请关照我的公众号: