一、简介
迪杰斯特拉(Dijkstra)算法和弗洛伊德(Flyod)算法均是用于求解有向图或无向图从一点到另外一个点最短路径。
二、Dijkstra
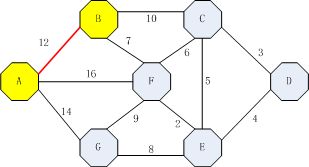
迪杰斯特拉算法也是图论中的明星算法,主要是其采用的动态规划思想,使其在数据结构、算法、离散数学乃至运筹学中都扮演重要的角色。以下图为例:
以A为起点,首先走一步,共有三条边,分别如下:
AB(12),AF(16),AG(14)其中最短的是节点B,将AB(12)放入辅助向量。
接着,各节点均继续向下走,此时可以找出4条边。
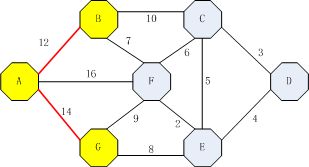
ABC(22),ABF(19),AF(16),AG(14),同样找出最小值放入向量中。{AB(12),AG(14)}
此后步骤完全相同
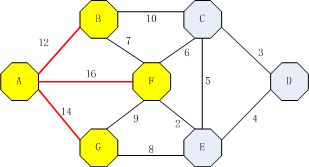
ABC(22),ABF(19),AF(16),AGF(23),AGE(22),选中AF(16)。
同样,接下来的步骤有:ABC(22),AFC(22),AFE(18),AGE(22),选中AFE(18);
ABC(22),AFC(22),AFEC(23),AFED(22),这种情况随便选取一个最小值,以ABC(22)为例;
ABCD(25),AFED(22)选中后者,至此,已经完全找到A和所有节点之间的最短路径及最短路径的长度。
最短路径向量为{AB(12),AG(14),AF(16),AFE(18),ABC(22),AFED(22)}
三、Floyd
弗洛伊德是另外一种求最短路径的方式,与迪杰斯特拉算法不同,弗洛伊德偏重于多源最短路径的求解,即能迪杰斯特拉能够求一个节点到其余所有节点的最短路径,但是弗洛伊德能够求出任意两个节点的最短路径,当然迪杰斯特拉重复N次也能达到目标。两种方式的时间复杂度均为O(n^3),但弗洛伊德形式上会更简易一些。
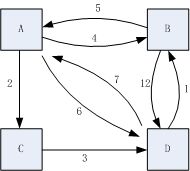
以下面的有向有权图为例:
老版visio不知道为啥这么糊?
首先写出图的邻接矩阵Adj
| A | B | C | D | |
| A | 0 | 4 | 2 | 6 |
| B | 5 | 0 | ∞ | 12 |
| C | ∞ | ∞ | 0 | 3 |
| D | 7 | 1 | ∞ | 0 |
若想缩短两点间的距离,仅有一种方式,那就是通过第三节点绕行,如果我们假设仅能通过A点绕行,那么仅需判断是否现有的距离Adj[i][j]小于Adj[i][1]+Adj[1][j]的距离,如果有更短的选择,那么进行更新就好了。首先第一行和第一列肯定不会更新,然后对角线也不必更新。【其实通过观察可以知道,第三行也不会进更新,因为C根本无法绕到A】
| 0 | 4 | 2 | 6 |
| 5 | 0 | 7 | 11 |
| ∞ | ∞ | 0 | 3 |
| 7 | 1 | 9 | 0 |
接下来,开放绕行节点2,那么就相当于可以经过节点1和2进行绕行。更新条件是Adj[i][j]>Adj[i][2]+Adj[2][j],除去第2行,第2列和对角线不需要进行判断。可以到D到C通过B-A会比仅通过A更短。
| 0 | 4 | 2 | 6 |
| 5 | 0 | 7 | 11 |
| ∞ | ∞ | 0 | 3 |
| 6 | 1 | 8 | 0 |
然后开放节点3.
| 0 | 4 | 2 | 5 |
| 5 | 0 | 7 | 10 |
| ∞ | ∞ | 0 | 3 |
| 6 | 1 | 8 | 0 |
最后开放节点4.
| 0 | 4 | 2 | 5 |
| 5 | 0 | 7 | 10 |
| 9 | 4 | 0 | 3 |
| 6 | 1 | 8 | 0 |
最短路径不适用于负权回路,或负权环,因为每次绕行都会减小最短路径,因此负权回路或者说负权环不存在最短路径。