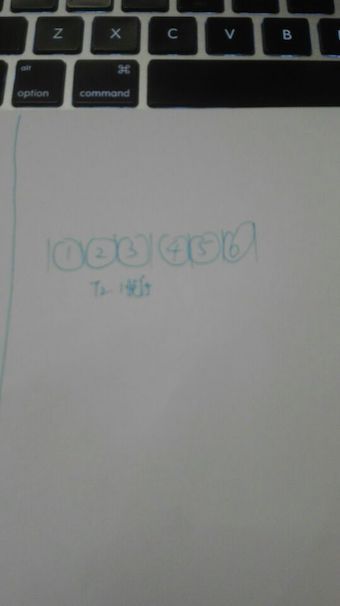TZ:我们恐惧的往往不是黑暗,而是光明
一 : 科普一分钟
什么是数据结构和算法,二者有和联系呢.
其实一种是数据存储的方式,一种是一种实现功能的手段.
我最近经常做饭,打个比方,就好比做菜一样,我们所用的食材就是数据结构,我们做同样的菜,食材有新鲜的有不新鲜的,肉质有老的有嫩的,同样算法好比厨师的厨艺,有高手和菜鸟,两者的配合会产生各种奇妙的结果,所以算法和数据结构 是程序的重要组成部分.
二 : 数据结构简述和举例
1. 概述:何为数据结构?
数据结构其实就是计算机存储,组织数据的方式.
相互之间存在一种或者多种特定关系的数据元素的集合
2. 常见的数据结构有哪些?
大家都学过数据结构这门课程,接下来我们来复习一下,我们都学过哪些数据结构.
(1) 线性表
包括我们常用的数组,链表,栈,和队列.
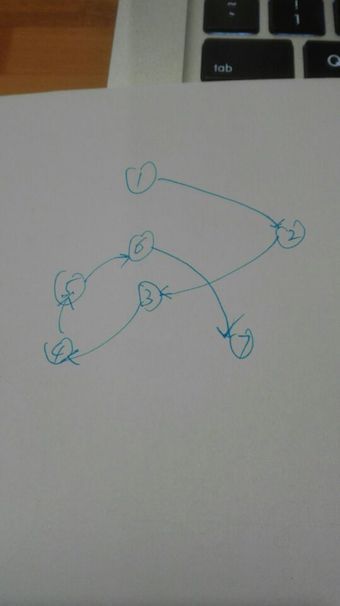
(2)树
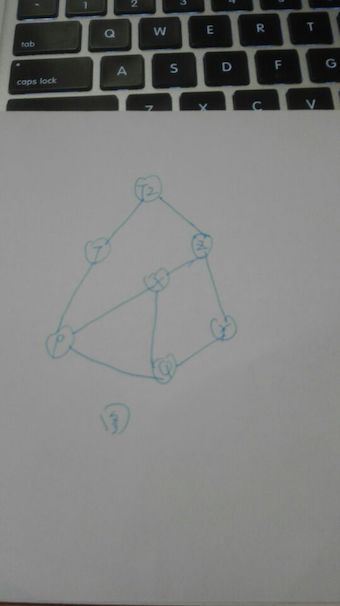
(3)图
3.常见的逻辑结构
什么是逻辑结构?个人理解就是有点"纸上谈兵"的意思,类似于草图或者说是思路结构
(1)集合结构 : 把杂乱的数据放进一个大锅里.
(2)线性结构 : 内存是连续的,类似于"铁索连环"
(3)树形结构 : 这个结构的特点就是....暂时理解像一颗树就好了
(4)图形结构 : 这个结构特点内存可以是连续的 也可以是不连续的
4.存储结构
说完了逻辑结构,我们说说存储结构,
(1) 顺序存储结构
(2)链式存储结构
- 队列
假如此时我们做一个解密算法
把一个数据串 第一个数扔掉,第二个数放到尾部,第三个数扔掉,第四个数放到尾部.....等等, 删掉的数按照移除顺序就是我们要的结果 如何实现呢?
这其实就是队列 ,队列是先进先出的,就好像我们排队买票,先站排的人最先买到票,最先离开,好像两头开口的一个通道.
我们用head 来标注 队列头 用tail 来标注队列尾部
注意 这里说的队尾 是值 尾部后+ 1 的位置
#include
int main()
{
int q[102] = {0,6,3,1,7,5,8,2,9,4},head,tail;
//初始化队列
head = 1;
tail = 10;
while(head < tail){
//打印队首
printf("%d",q[head]);
//出队
head ++
//将新队首数添加到队尾
q[tail] = q[head];
tail++;
//再次队首移除出队
head++
}
return 0;
}
6.栈
简单的说一下栈,我们吃的薯片或者弹夹,都类似栈,先进后出.
现在我们做个简单的小例子简单分析一下
做一个判断一个串 是否是回文
什么是回文, AABB ,ABBA ,ABCBA这种对称的叫回文
我们用一个指向栈顶的变量top
#include
#include
char a[101],s[101];
int i,len,mid,next,top;
gets(a)//读入一个串
len = strlen(a);
mid = len/2 - 1;
top = 0;
//mid前面数一次入栈
for(i = 0; i <= mid ;i++){
s[++top] = a[i];
}
//判断奇偶性
if(len%2 == 0)
next = mid + 1;
else
next = mid + 2;
//匹配
for(i = mext ; i - 链表
每一个链表的节点有两个部分组成,左边的部分存放的是具体的数值,右边存放的是下一个节点的地址.我们可以用一个结构体来描述它
struct node{
int data;
struct node *next;
}
现在实现 插入某个数到序列里,简单来说就是拆链和补链的过程.
#include
#include
struct node{
int data;
struct node *next;
};
int main(){
struct node *head,*p,*q,*t;
int i,n,a;
scanf("%d",&n);
head = NULL;//初始化
for(i = 1;i <= n;i++)
{
scanf("%d",&a);
//动态申请空间
p = (stuct node*)malloc(sizeof(stuct node));
p->data = a;//存放到当前节点
p ->next = NULL;
if(head ==NULL){
head = p;//创建第一个节点
}else{
q->next= p;
}
q = p;
//输入插入的数
scanf("%d",&a);
t = head;
while(t != NULL){
if(t->next ==NULL || t-> next->data > a){
p = (struct node*)malloc(sizeof( struct node));
//核心
p->data = a;
p->next= t->next;
t->next = p;
break;
}
t= t->next;
}
}
//输出
t = head
while(t !=NULL){
printf("%d",t->data);
t= t->next;
}
return 0;
}
对于数据结构和其存储代码只是简单描述,日后慢慢讲解.
三 : 算法简述和常用基础算法-排序
在工作中和学习中我们经常听到算法算法的,在上学的时候我们通常会学习算法这门单独学科的课程,讲的主要是,通过计算机语言编程解决一些和应用题一样的一些问题.
好,算法可以理解为是一种手段,或者一种解决方式,一系列的计算步骤,用来将输入数据转化为输出结果
1.算法的意义
(1)用于解决特定的问题
(2)解决同一个问题的不同算法的效率常常相差很大,这种差距的影响往往比硬件和软件方便的差距还要大.
2. 常用算法
(1)排序
(2)加密
3. 算法的优劣
怎样科学的评判一个算法的优劣,算法那么重要,不同的算法会很大程度上影响运行效率
时间复杂度 : 估算程序指令的执行次数
空间复杂度 估算所需占用的存储空间
这两个的计算方式我们以后的博客仔细讲解
4. 算法的优化方向
(1)用尽量少的内存空间
(2)用尽量少的执行步骤
(3)空间换时间
(4)时间换空间
5. 排序算法
(1)桶排序
1965年有两个大神, E.J Issac 和 R.C Singleton 提出来的基本思想.
下面简单总结一下这种算法的思想
#include
int main()
{
int a[10] , i,j,t;
for (i = 0 ; i <= 10 ; i++)
{
//初始化一下数组
a[i] = 0;
};
//循环输入7个数 对应的数字放到对应的桶中
for (int i = 0 ; i <7; i++ )
{
scanf("%d",&t);
a[t]++;
};
//输出打印
for(i = 0; i<= 10;i++){
for(j = 0;j <= a[i]; j++)
printf("%d",i);//每个桶中的数出现几次就打印几次
};
return 0;
}
总结分析 : 这是一个简化版的桶排序实际上桶排序要复杂很多这里就是和大家分析一下思路,下面画一个图来捋顺一下
每个桶的号码就是存放自己的专属数字,比如说1号桶专门存放的就是数字 1 5号桶专门存放 数组 5 初见几次 就往对应的桶里面 增加一次,也就是代码中的 a[t]++;
可以看的出来这种算法需要的空间很大,也就是说,我们要准备很多的 桶 这点并不可取
接下来看看其时间复杂度O(M+N) (计算方式以后博客会说明)
(2)冒泡排序
1956 年就有人曾经研究过冒泡排序,之后很多人研究改进过,但结果都令人失望,正如 高德纳 所说 冒泡排序除了它迷人的名字和导致了某些有趣的理论问题这一事实之外,似乎没什么值得推荐的
#include
int main(){
int a[100],i,j,t,n;
//输入n 个数存放到数组 a中
for(i = 0 ; i <= n ; i++){
scanf("%d",&a[i]);
};
//冒泡排序交换核心
for(i = 0 ; j <= n-1;i++){
for(j = 1 ; j < n - i;j++)
{
if( a[j] < a[j+1] ){
t = a[j]; a[j] = a[j+1]; a[j+1] = t;
}
}
}
//输出结果
for(i = 0 ;i <= n;i++){
printf("%d".a[i]);
}
return 0;
}
总结 : 冒泡排序就是两两交互比较大小,核心代码中的外层循环 是 走的 趟 数 控制交换了几趟,每一趟都能决定出一个最大的数 或者 最小的数 ,为什么是 n-1 因为最后一趟不用跑也确定了,因为就剩下那一个数了,同理内层循环 n - i 因为每趟交换 确定了一个数 ,所以我们内层循环 的时候 就要 排除那个已经 确定的 数.
接下来看看 冒泡排序 的时间复杂度 ->O(N²)
(3)快速排序
1960年 东尼霍尔 提出了快速排序 ,之后又有人做了优化.
思路 : 简单排序就是确定一个数 基数 让基数左边的数小于基数(这里说的是递增),让基数右边的数大于基数,
然后再去基数左边做同样操作 ,基数右边做同样操作
接下来上图来分析一下
图中 (1) 我们通常把首个数设置为基数 我们在序列左边放了一个检索 i 在 序列 右边放了一个检索 j 进行检索
当i 发现了 比 '6' 大的数则停下,当 j 发现了 比 6 小的数则停下,然后 把发现的数交换位置 如图(2)
交换完毕 i 和 j 继续移动 如图(3) 继续交换 最后 i 和 j 相遇 检索完毕
最后把 3 和 6 交换位置,以 6为基数的 检索结束 ,接下来 6 左边的数 和 6 右边的数进行 同理操作
#include
int a[101],n;
//我们把排序封装成方法 参数 分别是 左边启点 和 右边启点
void quicksort (int left,int right){
int i,j,t,temp;
if(left > right)
return;
};
temp = a[left];//确定基数
i = left;
j = right;
while(i != j){
//右边先开始检索
while( a[j] >= temp && i < j)
j--;
}
//从左往右检索
while( a[i] <= temp && i < j ){
i++
}
//交换两个数的位置
if( i < j) //没有相遇
{
t = a[i];
a[i] = a[j];
a[j] = t;
}
}
//基数归位
a[left] = a[i];
a[i] = temp;
quicksort(left,i-1);//处理基数左边的
quicksort(i+1,right);//处理基数右边的
return;
}
int main()
{
int i,j;
//读取数据
scanf("%d",&n);
for(i = 1;i < n;i++)
scanf("%d",&a[1]);
}
//调用
quicksort(1,n);
//输出
for(i = 1; i <= n ;i++){
printf("%d", a[i]);
}
return 0;
总结 : 为什么 j 要先移动,而 i 要后移动呢
因我我们把基数设置在了左边,我们假设一种特殊情况,就是数据序列已经是从小到大拍好了的,假如我们从左边开始检索,因为基数在左边,循环条件可订货满足,所以,i 肯定移动到下一个,所以就发生了错误,所以我们要右j边先移动.
四 : 总结
简单的聊过了数据结构和算法,一个好的程序,我们不仅要考虑它的运行速度,也要配上好的数据结构,也就是数据的存储方式,数据结构往往配合着算法的使用 更佳炫酷.