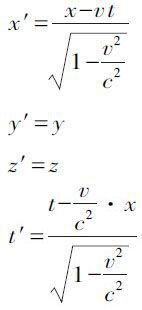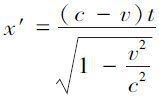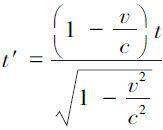今天咸鱼做了一把死,选择读了《狭义与广义相对论浅说》。读了两遍以后。我默默的掏出了那根1992年的棒棒糖,静静的仰望星空......好了不扯了,下面来说说咸鱼认为看懂的部分,如果有什么说错的地方欢迎指正!(推导部分以原文为主)
狭义相对论核心问题为光速在两个惯性系统中(假设一个静止,一个匀速直线。)速度值是相同的,这是实验得出的结论,那么问题就来了。如果经过经典力学的推导在绝对的时空观下,如果光速相同,那么这两个惯性系统必须相对静止。这很明显和前面(一个静止一个匀速)矛盾。那么很明显,要么是光速相同错了,要么是绝对的时空观错了!但是经过多方测量,确实光速没有测错,于是爱因斯坦决定放弃绝对的时空观。看下面这个例子。
假设有一列很长的火车,以恒速v沿着图所标明的方向在轨道上行驶。如果是绝对的时空观,那么在火车上发生的事,对于铁路路基也是同时发生的。这点没问题吧。好,那按照经典力学来具体推导对于铁路路基来说是同时的两个事件(例如A、B两处同时发生雷击),对于火车来说是否也是同时的呢?
当我们说A、B两处雷击相对于路基而言是同时的,我们的意思是:在发生闪电的A处和B处所发出的光,在路基A→B这段距离的中点M相遇。但是事件A和B也对应于火车上的A点和B点。令M′为在行驶中的火车上A→B这段距离的中点。正当雷电闪光发生的时候,点M′自然与点M重合,但是点M′以火车的速度v向图中的右方移动。如果坐在火车上M′处的一个观察者并不具有这个速度,那么他就总是停留在M点,雷电闪光A和B所发出的光就同时到达他这里,也就是说正好在他所在的地方相遇。可是实际上(相对于铁路路基来考虑)这个观察者正在朝着来自B的光线急速行进,同时他又是在来自A的光线的前方向前行进。因此这个观察者将先看见自B发出的光线,后看见自A发出的光线。所以,把列车当作参考物体的观察者就必然得出这样的结论,即雷电闪光B先于雷电闪光A发生。这样我们就得出以下的重要结果:
对于路基是同时的若干事件,对于火车并不是同时的,反之亦然(同时性的相对性)。每一个参考物体(坐标系)都有它本身的特殊的时间;除非我们讲出关于时间的陈述是相对于哪一个参考物体的,否则关于一个事件的时间的陈述就没有意义。
这里出现的问题在于两个经典力学的假设
(1) 两事件的时间间隔(时间)与参考物体的运动状况无关。
(2) 一刚体上两点的空间间隔(距离)与参考物体的运动状况无关。
如果放弃了这个假设那么问题就消失了。因为本来时间就不同!那么问题又来了,我们既要相对于火车又要相对于路基来谈地点和时间,如果放弃了经典力学我们应该如何描述。如果我们已知一事件相对于铁路路基的地点和时间,如何求出该事件相对于火车的地点和时间呢?转化一下就进入了本质问题:光速恒定!
我们能否设想,在各个事件相对于一个参考物体的地点和时间与各该事件相对于另一个参考物体的地点和时间之间存在着这样一种关系,使得每一条光线无论相对于路基还是相对于火车,它的传播速度都是c呢?
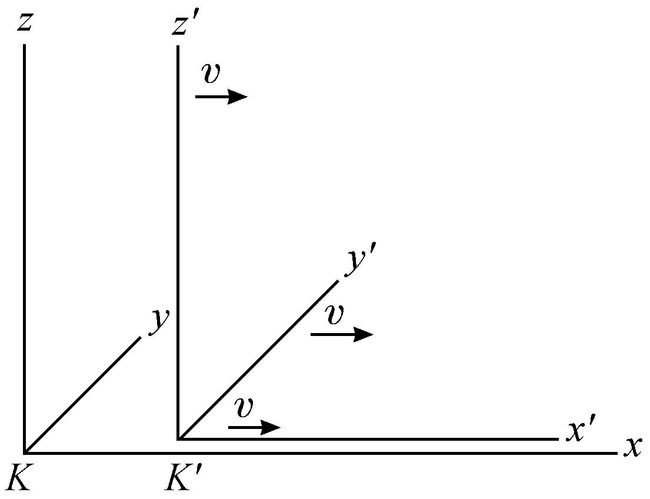
如图
图2K的x,y,z,t诸量值已经给定,K′的x′,y′,z′,t′诸量值为何?在选定关系式时,无论是相对于K或是相对于K′,对于同一条光线而言(当然对于每一条光线都必须如此)真空中光的传播定律必须被满足。若这两个坐标系在空间中的相对取向如图所示,这个问题就可以由下列方程组解出:
这个方程组称为“洛伦兹变换”。(具体推导太长,大家有兴趣的可以自行推导核心就是光速不变导不出了的少年可自行百度洛伦兹变换。)
如果我们不根据光的传播定律,而根据旧力学中所隐含的时间和长度具有绝对性的假定,那么我们所得到的就不会是上述方程组,而是如下的方程组:
x′=x-vt
y′=y
z′=z
t′=t
这个方程组通常称为“伽利略变换”。在洛伦兹变换方程中,我们如以无穷大值代换光速c,就可以得到伽利略变换方程。
通过下述例示,我们可以很容易地看到,按照洛伦兹变换,无论对于参考物体K还是对于参考物体K′,真空中光的传播定律都是被满足的,例如沿着正x轴发出一个光信号,这个光按照下列方程前进
x=ct
亦即以速度c前进。按照洛伦兹变换方程,x和t之间有了这个简单的关系,则在x′和t′之间当然也存在着一个相应的关系。事实也正是如此:把x的值ct代入洛伦兹变换的第一个和第四个方程中,我们就得到:
这两方程相除,即直接得出下式:
x′=c t′
亦即参照坐标系K′,光的传播应当按照此方程式进行。由此我们看到,光相对于参考物体K′的传播速度同样也是等于c。对于沿着任何其他方向传播的光线我们也得到同样的结果。当然,这一点是不足为奇的,因为洛伦兹变换方程就是依据这个观点推导出来的。
从上面的式子能推导出一个现在路人皆知的结论那就是没有超光速!看下面!
那么著名的不能超光速是怎么出来的呢!
假设如图2所示。我沿着K′的x′轴放置一根米尺,令其一端(始端)与点x′=0重合,另一端(末端)与点x′=1重合。问米尺相对于参考系K的长度为何?要知道这个长度,我们只须求出在参考系K的某一特定时刻t、米尺的始端和末端相对于K的位置。借助于洛伦兹变换第一方程,该两点在时刻t=0的值可表示为
两点间的距离为
。但米尺相对于 K以速度 v运动。因此,沿着其本身长度的方向以速度 v运动的刚性米尺的长度为具有极限速度的意义,任何实在的物体既不能达到也不能超出这个速度。
至于广义相对论,说实话咸鱼并没有看懂,书中叙述也较为简略,这里为了不误人子弟就不多说了。下面说说书中的其他思想与个人感想。
哲学和认识论的研究极大地促进了爱因斯坦相对论的创立。本书认为休谟的时空观念直接影响了爱因斯坦。休谟认为,空间观念是建立在对象的排列基础上,这种对象是可触知的;而时间观念是建立在对象的连续的基础上,这种对象是能够变化的,可觉察的。马赫的《力学史评》帮助爱因斯坦扫除了机械自然观和力学先验论的思想障碍,认识到牛顿的绝对时间和绝对空间等概念已经不适应科学的发展。而期间还有很多理论的碰撞。比如世界著名物理学家惠特克就认为爱因斯坦只是把庞加莱和洛伦兹的相对性理论稍加扩充而重新提了出来。但是实际上两者有本质差别。并且相对论的发明也是历经波折,爱因斯坦一度没有找到解决问题的数学工具,最后是在数学家格罗斯曼的大力帮助下从里奇和勒维·契维塔的绝对微分学以及黎曼几何中找到了合适的数学工具。才在1913年和格罗斯曼完成了论文“广义相对论和引力理论纲要”,其中物理部分由爱因斯坦执笔,数学部分由格罗斯曼执笔。广义相对论的大门才打开。而相对论被人们接受也经过了比较漫长的时间。历经波折.........(不知道是我的问题还是书的问题,个人认为书中的序部分写的比较难读,逻辑比较难以理解,这里就不强行解释了。不知道是作者的原因还是咸鱼功力不够。全书正文只有25%左右,其他都是辅助阅读的东西。即使这样,咸鱼依旧读的比较难受。书总的来说是好书,有毅力的少年可以去试试!)
下面说说个人体悟。
从书中咸鱼很好的体会到了科学的渐进式发展与聚合性,通过对前人的修正而不断提出新的概念而不是凭空出现一个理念。也理解了为什么现实世界比想象世界更疯狂。明白了“我们都同意你的理论是疯狂的。我们的分歧在于它是否疯狂到了足以有机会是正确的程度”这句话是多么的正确。谁能凭空想到我们的时间居然是个速度函数!这是多么疯狂的一件事!
看这本书的时候,也渐渐想到了一个问题,我们学到的知识是多么的伟大,现在我们看起来理说当然的事情,是多少人的付出。想到这里,咸鱼不禁为自己在大学里的学渣做派表示深深的后悔和遗憾,现在对世界充满了好奇。但是还有很多理解世界所必须的工具要补,这些本来是该在大学完成的。虽然现在还不晚,但是逝去的还是逝去了。愿每个人珍惜现在,每天进步一点点........