作者:何庆红(北京大学中国卫生经济研究中心)
连享会:(知乎 | | 码云 | CSDN)
Stata连享会 计量专题 || 精品课程 || 推文 || 公众号合集
2020寒假Stata现场班 (北京, 1月8-17日,连玉君-江艇主讲),「+助教招聘」
本推文介绍合成控制方法及其 Stata 的实现命令。合成控制方法(Synthetic Control Method)由Abadie and Gardeazabal (2003)提出。目前,该方法已被广泛使用。
1. 背景介绍
经济学家常要评估某政策或事件的效应。此政策可能实施于某国家或地区(省、州或城市)。为此,常使用“鲁宾的反事实框架”(Rubin's counterfactual framework),即假想该地区如未受政策干预将会怎样,并与事实上受到干预的实际数据进行对比,二者之差即为“处理效应”(treatment effect,借用医学术语)。常用解决方法是,寻找适当的控制组(control group),即在各方面都与受干预地区相似却未受干预的其他地区,以作为处理组(treated group,即受到干预的地区)的反事实替身(counterfactuals)。
比如,要考察仅在A市实施的某政策效果,自然会想到以之相近的B市作为控制地区;但B市毕竟与A市不完全相同。或可用其他城市(B市、C市、D市)构成A市的控制组,比较B市、C市、D市与A市在政策实施前后的差别,此方法也称“比较案例研究”(comparative case studies)。但如何选择控制组通常存在主观随意性(ambiguity),而B市、C市、D市与A市的相似度也不尽相同。
为此,Abadie and Gardeazabal (2003)提出“合成控制法”(Synthetic Control Method)。其基本思想是,虽然无法找到A市的最佳控制地区,但通常可对若干大城市进行适当的线性组合,以构造一个更为优秀的“合成控制地区”(synthetic control region),并将“真实A市”与“合成A市”进行对比,故名“合成控制法”。合成控制法的一大优势是,可以根据数据(data-driven)来选择线性组合的最优权重,避免了研究者主观选择控制组的随意性。
- 合成控制方法(Synthetic Control Method)的优点
- 作为一种非参数的方法,是对传统的双重差分法DID的拓展
- 通过数据驱动确定权重,减少了主观选择的误差,避免了政策内生性问题
- 通过对多个控制对象加权来模拟目标对象政策实施前的情况,不仅可以清晰地反映每个控制对象对“反事实”事件的贡献,同时也避免了过分外推
- 可以对每一个研究个体提供与之对应的合成控制对象,避免平均化的评价,不至于因各国政策实施时间不同而影响政策评估结果,避免了主观选择造成的偏差
- 研究者们可在不知道实施效果的情况下设计实验
连享会计量方法专题……
2. 合成控制法原理
原理介绍请看以下链接:
Stata: 合成控制法程序
合成控制法:一组文献
合成控制法简介及代码
3. 合成控制法的 Stata 实现
3.1 命令安装
在 Stata 命令窗口中输入如下命令即可自动安装 synth 命令:
ssc install synth, replace
3.2 语法格式
synth 的基本语法格式如下:
synth depvar predictorvars(x1 x2 x3) , trunit(#) trperiod(#) ///
[ counit(numlist) xperiod(numlist) mspeperiod() ///
resultsperiod() nested allopt unitnames(varname) ///
figure keep(file) customV(numlist) optsettings ]
具体解释如下:
- “ y ”为结果变量(outcome variable)
- “ x1 x2 x3 ”为预测变量(predictors)。
- 必选项“ trunit(#) ”用于指定处理地区(trunit表示 treated unit)。
- 必选项“ trperiod(#) ”用于指定政策干预开始的时期(trperiod表示 treated period)。
- 选择项“ counit(numlist) ”用于指定潜在的控制地区(即donor pool,其中counit表示 control units),默认为数据集中的除处理地区以外的所有地区。
- 选择项“ xperiod(numlist) ”用于指定将预测变量(predictors)进行平均的期间,默认为政策干预开始之前的所有时期(the entire pre-intervention period)。
- 选择项“ mspeperiod() ”用于指定最小化均方预测误差(MSPE)的时期,默认为政策干预开始之前的所有时期。
- 选择项“ figure ”表示将处理地区与合成控制的结果变量画时间趋势图,而选择项“resultsperiod()”用于指定此图的时间范围(默认为整个样本期间)。
- 选择项“ nested ”表示使用嵌套的数值方法寻找最优的合成控制(推荐使用此选项),这比默认方法更费时间,但可能更精确。在使用选择项“nested”时,如果再加上选择项“ allopt ”(即“ nested allopt ”),则比单独使用“nested”还要费时间,但精确度可能更高。
- 选择项“ keep(filename) ”将估计结果(比如,合成控制的权重、结果变量)存为另一Stata数据集(filename.dta),以便进行后续计算。
3.3 加州控烟案例
背景:1988年11月美国加州通过了当代美国最大规模的控烟法(anti-tobacco legislation),并于1989年1月开始生效。该法将加州的香烟消费税(cigarette excise tax)提高了每包25美分,将所得收入专项用于控烟的教育与媒体宣传,并引发了一系列关于室内清洁空气的地方立法(local clean indoor-air ordinances),比如在餐馆、封闭工作场所等禁烟。Abadie et al. (2010)根据美国1970-2000年的州际面板数据,采用合成控制法研究美国加州1988年第99号控烟法(Proposition 99)的效果。
. sysuse smoking (打开数据集)
. xtset state year (设为面板数据)
. synth cigsale retprice lnincome age15to24 beer ///
cigsale(1975) cigsale(1980) cigsale(1988), ///
trunit(3)trperiod(1989) xperiod(1980(1)1988) ///
figure nested keep(smoking_synth)
具体解释如下:
-
cigsale(1975)cigsale(1980)cigsale(1988)分别表示人均香烟消费在 1975、1980 与 1988 年的取值。 - 必选项 “
trunit(3)” 表示第 3 个州(即加州)为 处理组 (实验对象)。 - 必选项 “
trperiod(1989)” 表示控烟法在 1989 年开始实施 (政策实施时点)。 - 选择项 “
xperiod(1980(1)1988)” 表示将预测变量在 1980-1988 年期间进行平均,其中 “1980(1)1988” 表示始于1980年,以 1 年为间隔,而止于 1988 年;其效果等价于 “1980 1981 1982 1983 1984 1985 1986 1987 1988”,而前者的写法显然更为简洁。 - 选择项 “
keep(smoking_synth)”将估计结果存为 Stata 数据集 smoking_synth.dta (自动存放于当前工作路径下)。
由 Table2 可知,大多数州的权重为 0,而只有以下五个州的权重为正,即 Colorado (0.161),Connecticut (0.068),Montana (0.201),Nevada (0.235) 与 Utah (0.335)。我们随后会用这五个州的实际香烟消费量的加权平均值作为 合成加州 的替代指标。
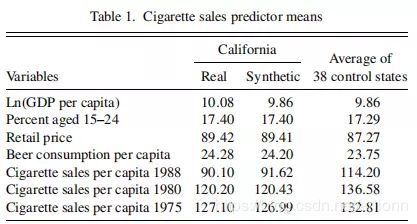
考察加州与合成加州的预测变量是否接近:
从上表 Table1 可知,加州与合成加州的预测变量均十分接近,故合成加州可以很好地复制加州的经济特征。然后比较二者的人均香烟消费量在 1989 年前后的表现:
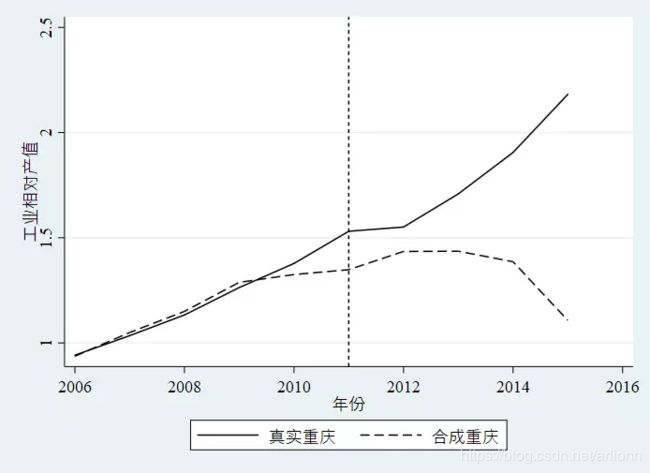
从上图可知,在 1989 年控烟法之前,合成加州的人均香烟消费与真实加州几乎如影相随,表明合成加州可以很好地作为加州如未控烟的反事实替身。在控烟法实施之后,加州与合成加州的人均香烟消费量即开始分岔,而且此效应越来越大。
紧接着,调用前面已存的数据集 smoking_synth.dta,计算加州与合成加州人均香烟消费之差(即处理效应),然后画图:
. use smoking_synth.dta, clear
*- 定义处理效应为变量 effect
* 其中, “_Y_treated” 与 “_Y_synthetic” 分别表示处理地区与合成控制的结果变量
. gen effect= _Y_treated - _Y_synthetic
. label variable _time "year"
. label variable effect "gap in per-capita cigarette sales (in packs)"
. line effect _time, xline(1989,lp(dash)) yline(0,lp(dash))
上图显示,加州控烟法对于人均香烟消费量有很大的负效应,而且此效应随着时间推移而变大。具体来说,在 1989-2000 年期间,加州的人均年香烟消费减少了 20 多包,大约下降了 25% 之多,故其经济效应十分显著(economically significant)。
连享会计量方法专题……
3.4 房产税对产业转移的影响:来自重庆和上海的经验证据
(研究背景请看原文链接)
. synth 工业相对产值 工业相对产值(2006(1)2010) 相对工资 ln人均GDP 财政支出占GDP比重 ln人口密度人平方公里 ///
ln年末金融机构存款余额万元 ln医院卫生院床位数张 ln国际互联网用户数户 工业相对产值(2006) 工业相对产值(2008) ///
工业相对产值(2010), trunit(26) trperiod(2011) nested fig
----------------------------------------------------------------------------------------------------------------------
Synthetic Control Method for Comparative Case Studies
----------------------------------------------------------------------------------------------------------------------
First Step: Data Setup
----------------------------------------------------------------------------------------------------------------------
Data Setup successful
----------------------------------------------------------------------------------------------------------------------
Treated Unit: 26
Control Units: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 27 28 29 30 31 32 33 34
----------------------------------------------------------------------------------------------------------------------
Dependent Variable: 工业相对产值
MSPE minimized for periods: 2006 2007 2008 2009 2010
Results obtained for periods: 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
----------------------------------------------------------------------------------------------------------------------
Predictors: 工业相对产值(2006(1)2010) 相对工资 ln人均GDP 财政支出占GDP比重 ln人口密度人平方公里
ln年末金融机构存款余额万元 ln医院卫生院床位数张 ln国际互联网用户数户 工业相对产值(2006) 工业相对产值(20008) 工业相对产值(2010)
----------------------------------------------------------------------------------------------------------------------
Unless period is specified
predictors are averaged over: 2006 2007 2008 2009 2010
----------------------------------------------------------------------------------------------------------------------
Second Step: Run Optimization
----------------------------------------------------------------------------------------------------------------------
Nested optimization requested
Starting nested optimization module
Optimization done
----------------------------------------------------------------------------------------------------------------------
Optimization done
----------------------------------------------------------------------------------------------------------------------
Third Step: Obtain Results
----------------------------------------------------------------------------------------------------------------------
Loss: Root Mean Squared Prediction Error
---------------------
RMSPE | .028082
---------------------
----------------------------------------------------------------------------------------------------------------------
Unit Weights:
-----------------------
Co_No | Unit_Weight
----------+------------
1 | 0
2 | .084
3 | 0
4 | 0
5 | 0
6 | .672
7 | 0
8 | 0
9 | 0
10 | 0
11 | 0
12 | 0
13 | .244
14 | 0
15 | 0
16 | 0
17 | 0
18 | 0
19 | 0
20 | 0
21 | 0
22 | 0
23 | 0
24 | 0
25 | 0
27 | 0
28 | 0
29 | 0
30 | 0
31 | 0
32 | 0
33 | 0
34 | 0
----------------------------------------------------------------------------------------------------------------------
Predictor Balance:
------------------------------------------------------
| Treated Synthetic
-------------------------------+----------------------
工业相对产值(2006(1)2010) | 1.150089 1.150037
相对工资 | 1.619055 1.013639
ln人均GDP | 9.817525 10.73459
财政支出占GDP比重 | .18338 .1116527
ln人口密度人平方公里 | 5.977395 6.399682
ln年末金融机构存款余额万元 | 18.25113 17.72419
ln医院卫生院床位数张 | 11.27253 10.37265
ln国际互联网用户数户 | 14.7616 13.70787
工业相对产值(2006) | .9416254 .9369883
工业相对产值(2008) | 1.132921 1.150078
工业相对产值(2010) | 1.377864 1.325148
------------------------------------------------------
4. 安慰剂检验
4.1 安慰剂检验一
Abadie et al. (2010) 认为,在比较案例研究中,由于潜在的控制地区数目通常并不多,故不适合使用大样本理论进行统计推断。为此,Abadie et al. (2010) 提出使用 “安慰剂检验” (placebo test)来进行统计检验,这种方法类似于统计学中的 “组合检验”(permutation test),适用于任何样本容量。
- “安慰剂”(placebo)一词来自医学上的随机实验,比如要检验某种新药的疗效。此时,可将参加实验的人群随机分为两组,其中一组为实验组,服用真药;而另一组为控制组,服用安慰剂(比如,无用的糖丸),并且不让参与者知道自己服用的究竟是真药还是安慰剂,以避免由于主观心理作用而影响实验效果,称为“安慰剂效应”(placebo effect)。
- 安慰剂检验借用了安慰剂的思想。具体到加州控烟法的案例,我们想知道,使用上述合成控制法所估计的控烟效应,是否完全由偶然因素所驱动?换言之,如果从donor pool随机抽取一个州(而不是加州)进行合成控制估计,能否得到类似的效应?
- 为此,Abadie et al. (2010)进行了一系列的安慰剂检验,依次将donor pool中的每个州作为假想的处理地区(假设也在1988年通过控烟法),而将加州作为控制地区对待,然后使用合成控制法估计其“控烟效应”,也称为“安慰剂效应”。通过这一系列的安慰剂检验,即可得到安慰剂效应的分布,并将加州的处理效应与之对比。
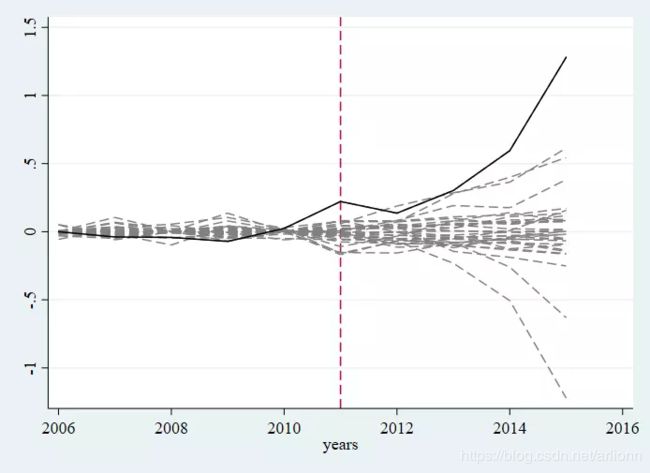
在上图中,黑线表示加州的处理效应(即加州与合成加州的人均香烟消费之差),而灰线表示其他38、34、29、19个控制州的安慰剂效应(即这些州与其相应合成州的人均香烟消费之差)。显然,与其他州的安慰剂效应相比,加州的(负)处理效应显得特别大。假如加州的控烟法并无任何效应,则在这39、35、30、20个州中,碰巧看到加州的处理效应最大的概率仅为 1/39 = 0.0256,1/35 = 0.0286,1/30 = 0.0333,1/20 = 0.05,而这都小于常用的显著性水平0.05,故初步可知黑线处理效应的确是加州控烟的效果。
****稳健性检验*****************************
//有效性检验(仅展示重庆房产税对工业相对产值影响的稳健性检验程序)
************************************稳健性检验一(工业相对产值为目标变量)************************************
//政策实施前均方预测误差的平方根
tempname resmat //设定一个临时矩阵叫做resmat
forvalues i = 1/35 { //这里的循环是指将1到4个州分别做一次合成控制,也就是把2-4州,分别当做处理组进行合成控制
synth 工业相对产值 相对工资 ln人均GDP 财政支出占GDP比重 ln人口密度人平方公里 ln年末金融机构存款余额万元 ///
ln医院卫生院床位数张 ln国际互联网用户数户 工业相对产值(2006) 工业相对产值(2008) 工业相对产值(2010), trunit(`i') ///
trperiod(2011) xperiod(2006(1)2010) mspeperiod
matrix `resmat' = nullmat(`resmat') \ e(RMSPE) //临时矩阵等于每个城市做处理进行合成控制时候的rmspe值
local names `"`names' `"`i'"'"' //设定暂元names 为 1 2 3 4 ''' 35
}
mat colnames `resmat' = "RMSPE" //临时矩阵的列名定义为RMSPE
mat rownames `resmat' = `names' // 临时矩阵的行名为names
matlist `resmat' , row("Treated Unit") //展示临时矩阵,并在行的打头表示为“treated unit”
** loop through units
** loop throu
//各城市预测误差分布图
forval i=1/35{
qui synth 工业相对产值 相对工资 ln人均GDP 财政支出占GDP比重 ln人口密度人平方公里 ln年末金融机构存款余额万元 ln医院卫生院床位数张 ln国际互联网用户数户 工业相对产值(2006) 工业相对产值(2008) 工业相对产值(2010), xperiod(2006(1)2010) trunit(`i') trperiod(2011) keep(synth_`i', replace)
}
forval i=1/35{
use synth_`i', clear
rename _time years
gen tr_effect_`i' = _Y_treated - _Y_synthetic
keep years tr_effect_`i'
drop if missing(years)
save synth_`i', replace
}
**
use synth_1, clear
forval i=2/35{
qui merge 1:1 years using synth_`i', nogenerate
}
**
**删除拟合不好的城市及上海市(干预组)
drop tr_effect_2 //删除天津
drop tr_effect_20 //删除武汉
drop tr_effect_35 //删除上海
local lp1
forval i=1/1 {
local lp1 `lp1' line tr_effect_`i' years, lpattern(dash) lcolor(gs8) ||
}
**
local lp2
forval i=3/19 {
local lp2 `lp2' line tr_effect_`i' years, lpattern(dash) lcolor(gs8) ||
}
local lp3
forval i=21/34 {
local lp3 `lp3' line tr_effect_`i' years, lpattern(dash) lcolor(gs8) ||
}
**create plot
twoway `lp1' `lp2' `lp3' || line tr_effect_26 years, ///
lcolor(black) legend(off) xline(2011, lpattern(dash))
连享会计量方法专题……
4.2 安慰剂检验二
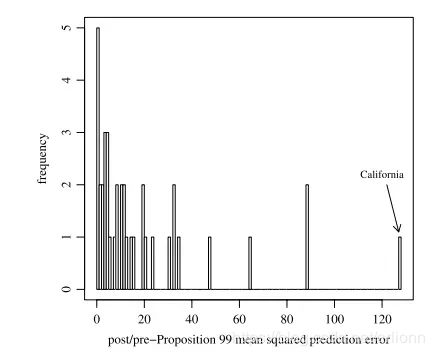
安慰剂检验的另一方式是直接将每个州“干预后的MSPE”与“干预前的MSPE”相比,即计算二者的比值。其基本逻辑如下。对于处理地区加州而言,如果控烟法有效果,则合成控制将无法很好地预测真实加州干预后的结果变量,导致较大的干预后MSPE。然而,如果在干预之前,合成加州就无法很好地预测真实加州的结果变量(较大的干预前MSPE),这也会导致干预后MSPE增大,故取二者的比值以控制前者的影响。如果加州控烟法确实有较大的处理效应,而其他州的安慰剂效应都很小,则应该观测到加州的“干预后MSPE”与“干预前MSPE”之比值明显高于其他各州,而这为下图所证实。
从上图可知,加州的干预后MSPE是干预前MSPE的大约130倍,高于所有其他38个州。如果加州控烟法完全无效,而由于偶然因素使得此比值在所有39州中最大的概率仅为 1/39 = 0.026。
连享会计量方法专题……
5. 参考资料
Abadie, A., Diamond, A., and J. Hainmueller. 2014. Comparative Politics and the Synthetic Control Method. American Journal of Political Science
Abadie, A., Diamond, A., and J. Hainmueller. 2010. Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California's Tobacco Control Program. Journal of the American Statistical Association
Abadie, A. and Gardeazabal, J. 2003. Economic Costs of Conflict: A Case Study of the Basque Country. American Economic Review
Vanderbei, R.J. 1999. LOQO: An interior point code for quadratic programming. Optimization Methods and Software 11: 451-484.
房产税对产业转移的影响:来自重庆和上海的经验证据
连享会计量方法专题……
关于我们
- Stata连享会 由中山大学连玉君老师团队创办,定期分享实证分析经验。
- 推文同步发布于 CSDN 、 和 知乎Stata专栏。可在百度中搜索关键词 「Stata连享会」查看往期推文。
- 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
- 欢迎赐稿: 欢迎赐稿。录用稿件达 三篇 以上,即可 免费 获得一期 Stata 现场培训资格。
- E-mail: [email protected]
- 往期精彩推文:一网打尽