传统的分布式算法
在了解redis分布式算法之前，最好先了解一下缓存中的一个应用场景，了解了这个应用场景之后，再来理解一致性哈希算法，就容易多了，也更能体现出一致性哈希算法的优点，那么，我们先来描述一下这个经典的分布式缓存的应用场景。
场景描述：
假设，我们有三台缓存服务器，用于缓存图片，我们为这三台缓存服务器编号为0号、1号、2号，现在，有3万张图片需要缓存，我们希望这些图片被均匀的缓存到这3台服务器上，以便它们能够分摊缓存的压力。也就是说，我们希望每台服务器能够缓存1万张左右的图片，那么，我们应该怎样做呢？如果我们没有任何规律的将3万张图片平均的缓存在3台服务器上，可以满足我们的要求吗？可以！但是如果这样做，当我们需要访问某个缓存项时，则需要遍历3台缓存服务器，从3万个缓存项中找到我们需要访问的缓存，遍历的过程效率太低，时间太长，当我们找到需要访问的缓存项时，时长可能是不能被接收的，也就失去了缓存的意义，缓存的目的就是提高速度，改善用户体验，减轻后端服务器压力，如果每次访问一个缓存项都需要遍历所有缓存服务器的所有缓存项，想想就觉得很累，那么，我们该怎么办呢？原始的做法是对缓存项的键进行哈希，将hash后的结果对缓存服务器的数量进行取模操作，通过取模后的结果，决定缓存项将会缓存在哪一台服务器上，这样说可能不太容易理解，我们举例说明，仍然以刚才描述的场景为例，假设我们使用图片名称作为访问图片的key，假设图片名称是不重复的，那么，我们可以使用如下公式，计算出图片应该存放在哪台服务器上：
hash（图片名称）% N
因为图片的名称是不重复的，所以，当我们对同一个图片名称做相同的哈希计算时，得出的结果应该是不变的，如果我们有3台服务器，使用哈希后的结果对3求余，那么余数一定是0、1或者2，没错，正好与我们之前的服务器编号相同，如果求余的结果为0， 我们就把当前图片名称对应的图片缓存在0号服务器上，如果余数为1，就把当前图片名对应的图片缓存在1号服务器上，如果余数为2，同理，那么，当我们访问任意一个图片的时候，只要再次对图片名称进行上述运算，即可得出对应的图片应该存放在哪一台缓存服务器上，我们只要在这一台服务器上查找图片即可，如果图片在对应的服务器上不存在，则证明对应的图片没有被缓存，也不用再去遍历其他缓存服务器了，通过这样的方法，即可将3万张图片随机的分布到3台缓存服务器上了，而且下次访问某张图片时，直接能够判断出该图片应该存在于哪台缓存服务器上，这样就能满足我们的需求了，我们暂时称上述算法为HASH算法或者取模算法，取模算法的过程可以用下图表示：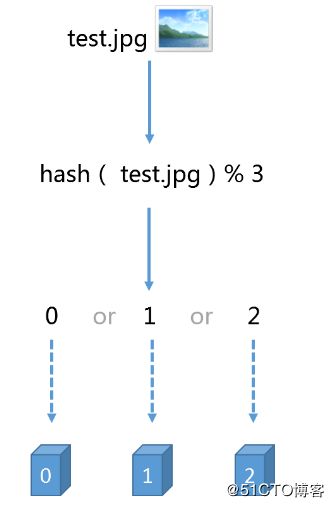
但是，使用上述HASH算法进行缓存时，会出现一些缺陷，试想一下，如果3台缓存服务器已经不能满足我们的缓存需求，那么我们应该怎么做呢？没错，很简单，多增加两台缓存服务器不就行了，假设，我们增加了一台缓存服务器，那么缓存服务器的数量就由3台变成了4台，此时，如果仍然使用上述方法对同一张图片进行缓存，那么这张图片所在的服务器编号必定与原来3台服务器时所在的服务器编号不同，因为除数由3变为了4，被除数不变的情况下，余数肯定不同，这种情况带来的结果就是当服务器数量变动时，所有缓存的位置都要发生改变，换句话说，当服务器数量发生改变时，所有缓存在一定时间内是失效的，当应用无法从缓存中获取数据时，则会向后端服务器请求数据，同理，假设3台缓存中突然有一台缓存服务器出现了故障，无法进行缓存，那么我们则需要将故障机器移除，但是如果移除了一台缓存服务器，那么缓存服务器数量从3台变为2台，如果想要访问一张图片，这张图片的缓存位置必定会发生改变，以前缓存的图片也会失去缓存的作用与意义，由于大量缓存在同一时间失效，造成了缓存的雪崩，此时前端缓存已经无法起到承担部分压力的作用，后端服务器将会承受巨大的压力，整个系统很有可能被压垮，所以，我们应该想办法不让这种情况发生，但是由于上述HASH算法本身的缘故，使用取模法进行缓存时，这种情况是无法避免的，为了解决这些问题，一致性哈希算法诞生了。
我们来回顾一下使用上述算法会出现的问题：
- 问题1：当缓存服务器数量发生变化时，会引起缓存的雪崩，可能会引起整体系统压力过大而崩溃（大量缓存同一时间失效）。
- 问题2：当缓存服务器数量发生变化时，几乎所有缓存的位置都会发生改变，怎样才能尽量减少受影响的缓存呢？
其实，上面两个问题是一个问题，那么，一致性哈希算法能够解决上述问题吗？我们现在就来了解一下一致性哈希算法。
redis分布式算法
redis使用的是 Consistent hashing 算法：
- Consistent hashing 是一致性hash算法
- Consistent hashing 算法早在1997年就在论文《Consistent hashing and random trees》中提出
这个算法有一个环形hash空间的概念，我们先来了解一下环形hash空间：
- 通常hash算法都是将value映射在一个32位的key值当中，那么把数轴首尾相接就会形成一个圆形，取值范围为0 ~ 2^32-1，这个圆形就是环形hash空间。如下图：
我们来看看如何把对象映射到环形hash空间：
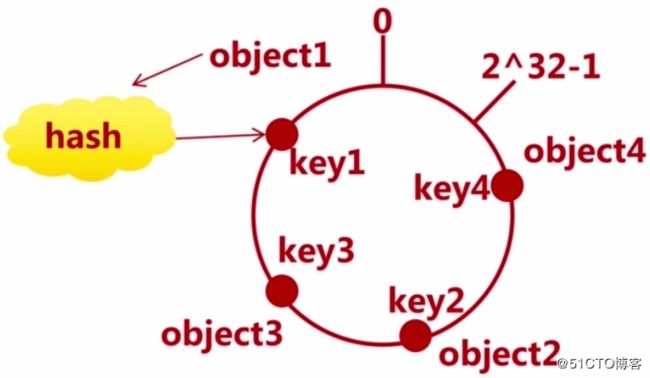
- 只考虑4个对象Object1 ~ Object4
- 首先通过hash函数计算出这四个对象的hash值key，这些对象的hash值肯定是会落在上述中的环形hash空间范围上的，对象的hash对应到环形hash空间上的哪一个key值那么该对象就映射到那个位置上，这样对象就映射到环形hash空间上了。如下图：
然后就是把cache映射到环形hash空间，cache就是我们的redis服务器：
- 基本思想就是将对象和cache都映射到同一个hash环形空间中，并且使用相同的hash算法进行计算，用伪码表示如下：
hash(cache A) = key A;
... ...
hash(cache C) = key C;计算出cache的hash值之后，就和对象一样映射到hash环形空间中对应的key上，使用图片表示如下：
可以看到，Cache和Obejct都映射到这个环形hash空间中了，那么接下来要考虑的就是如何将object映射到cache中。其实在这个环形hash空间进行一个顺时针的计算即可，例如key1顺时针遇到的第一个cache是cacheA，所以就将key1映射到cacheA中，key2顺时针遇到的第一个cache是cacheC，那么就将key2映射到cacheC中，以此类推。如下图：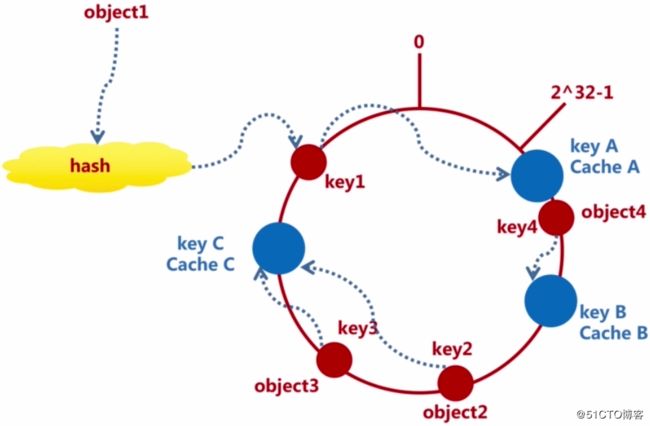
如果某一个cache被移除之后，那么object会继续顺时针寻找下一个cache进行映射。例如，cacheB被移除了，映射在cacheB中的object4就会顺时针往下找到cacheC，然后映射到cacheC上。如下图：
所以当移除一个cacheB时所影响的object范围就是cacheB与cacheA之间的那一段范围，这个范围是比较小的。如下图所标出的范围：
而当增加一个cache节点时也是同理，例如，在acheC和cacheB之间增加了一个cacheD节点，那么object2在顺时针遇到的第一个cache就是cacheD，此时就会将obejct2映射到cacheD中。如下图：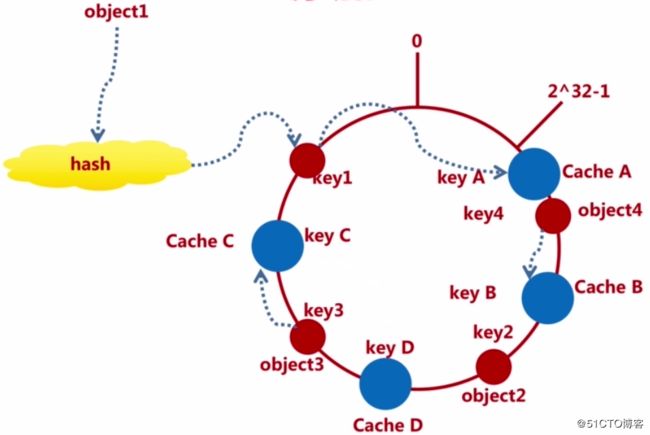
同样的，增加cache节点所影响的范围也就是cacheD和cacheB之间的那一段范围。如下图所标出的范围：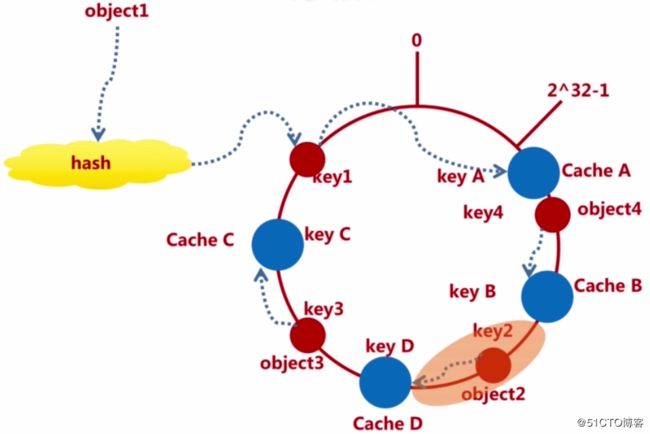
以上我们所讲解的都是理想中的情况，我们假设了所有的cache节点都是在环形hash空间上分布均匀的。但是我们都知道到理想很丰满现实很骨感，就像卖家秀和买家秀一种，总是会出现与实物不符的情况。
所以就有可能会出现cache节点无法均匀的分部在环形hash空间上。如下图：
可以看到，A、B、C节点都挤在了一块，按顺时针来计算，就会有大量的数据（object）映射到A节点上，从上图中来看就会有一大半的数据都映射到A节点上，那么A节点所承载的数据压力会十分大，B、C节点则无法得到很好的利用，几乎等同闲着没事干。这就是Hash倾斜性所导致的现象，无法保证在环形hash空间上绝对的分布均匀。
为了解决Hash倾斜性的问题，redis引入了虚拟节点的概念，虚拟节点相当于是实际节点的一个影子或者说分身，而且虚拟节点一般都比实际节点的数量要多。引入虚拟节点后，object不再直接映射到实际的cache节点中，而是先映射到虚拟节点中。然后虚拟节点会再进行一个hash计算，最后才映射到实际的cache节点中。所以虚拟节点就是对我们的实际节点进行一个放大，如下图：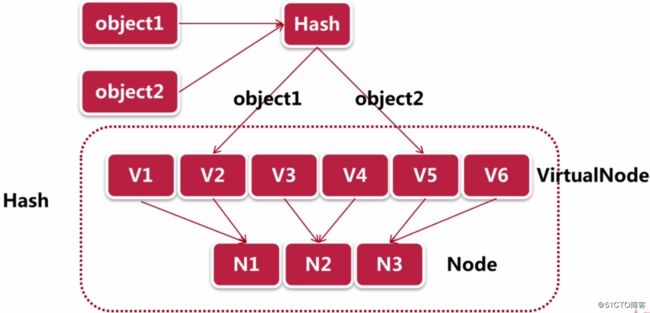
放到环形hash空间上进行表示，就是这样的，浅色为虚拟节点，深色为实际节点：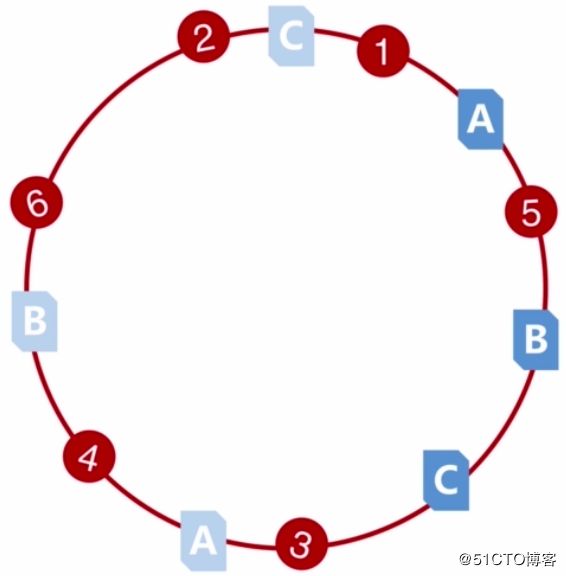
如上可以看到，这下分布就均匀了。这里只是作为演示，实际情况中的节点会更多，虚拟节点和实际节点是存在一定比例的。而且随着实际节点的增加，环形hash空间上的分布就会越来越均匀，当移除或增加cache时所受到的影响就会越小。
Consistent hashing 命中率计算公式：
(1 - n / (n + m)) * 100%n = 现有的节点数量
m = 新增的节点数量