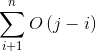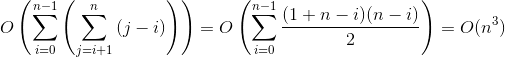Problem
Given a string, find the length of the longest substring without repeating characters.
Example:
Given "abcabcbb", the answer is "abc", which the length is 3.
Given "bbbbb", the answer is "b", with the length of 1.
Given "pwwkew", the answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.
给定一个字符串,找出最长的无重复字符的子字符串的长度。
Solution
Brute Force/暴力破解
逐个检查所有的子字符串,查看是否存在重复的字符。
假设有一个方法boolean allUnique(String substring)能够判断字符串中所有字符都是唯一的。那么将所有可能的子字符串传入allUnique方法。当结果返回true,则更新最长非重复子字符串的长度。
该方案的具体实现:
- 枚举出给定字符串的所有子字符串。假设子字符串的开始位置和结束位置以 i 和 j 表示,则0 ≤ i < j ≤ n(此处 j 为开区间)。通过使用两个嵌套循环 i (0 → n-1),j (i+1 → n),可以枚举出所有子字符串。
- 使用
set集合来检查一个字符串是否包含重复字符。遍历所有的子字符串,并且将其中的每个字符逐个放入set中。当放入字符前,需要检查其是否已存在于set中。如果该字符已存在则返回false,在放入所有的字符后返回true。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
return ans;
}
public boolean allUnique(String s, int start, int end) {
Set set = new HashSet<>();
for (int i = start; i < end; i++) {
Character ch = s.charAt(i);
if (set.contains(ch)) return false;
set.add(ch);
}
return true;
}
}
复杂度分析
- 时间复杂度:O(n3)。
为了验证下标是 [i,j) 的字符是否重复,需要扫描所有字符。因此,耗时是O(j - i)。
对于给定的i,计算每一个 j∈[i+1,n] 的合计为
因此,所有的时间开销为
- 空间复杂度:O(min(n,m))。使用了O(k)的空间来检查一个子字符串是否包含重复的字符,其中k为
set集合的大小。set集合的大小为字符串长度 n 和字符集大小 m 两者中较大的那个值。
Sliding Window/滑动窗口
在原先的方法中,通过循环检查子字符串来判断它是否包含重复的字符。然而这个过程并是不必要的。如果一个子字符串 sij 从下标 i 到 j-1 已经确认不存在重复的字符,则仅需要检查 s[j] 是否包含在 sij 中即可。
通过扫描子字符串来判断某个字符是否存在于其中,从而获得一个 O(n2) 算法。其实还可以做得更好。
通过使用一个HashSet作为滑动窗口,判断某个字符是否存在于当前字符串的时间复杂度为O(1)。
滑动窗口是处理
数组/字符串问题时的一个常用概念。窗口是指数组或字符串中从起始位置到终止位置的元素的集合,例如 [i,j)。滑动窗口是指两侧的边界值会向指定方向“滑动”。例如,若将 [i,j) 向右滑动1个元素,则它就成了 [i+1,j+1)。
回到当前的问题上,使用HashSet来存储当前窗口中的元素 [i,j),并且令 j 的初始值等于 i。然后向右滑动 j。如果 s[j] 对应的字符不在HashSet中,则继续滑动 j,直到字符 s[j] 存在于HashSet 中为止。此时,最长的非重复子字符串是 sij。如果对所有的 i 执行了上述操作,即可得到结果。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
Set set = new HashSet<>();
int ans = 0, i = 0, j = 0;
while (i < n && j < n) {
// try to extend the range [i, j]
if (!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans, j - i);
}
else {
set.remove(s.charAt(i++));
}
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(2n) = O(n)。在最坏的情况下每一个字符都将被 i 和 j 分别访问一次。
- 空间复杂度:O(min(m,n))。与前一个解法相同。需要O(k)的空间来存放滑动窗口,k为
Set集合的大小,且集合的大小为字符串长度 n 和字符集大小 m 两者中较大的那个值。
Sliding Window Optimized/滑动窗口优化
在上一个解法中最多使用 2n 步。实际上,它可以被优化到只需 n 步。通过使用一个map来存放字符的下标,而不仅仅是使用set来判断是否存在该字符。然后当发现重复字符时,可以将起始位置直接设置到该重复字符之后,直接跳过包含该重复字符的判断过程。
可以这么做的理由是,当 s[j] 在窗口 [i,j) 中存在一个重复且下标为 j' 的字符时,无需逐次移动 i。而是直接跳过 [i,j'] 范围内的所有元素,将起始位置 i 直接设置成 j' + 1。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map map = new HashMap<>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j)), i);
}
ans = Math.max(ans, j - i + 1);
map.put(s.charAt(j), j + 1);
}
return ans;
}
}
前面的实现中都没有考虑到字符串所使用的字符集。
如果提前知道字符集很小,可以使用int[]代替Map来作为字符和下标的映射表。
常见的映射表有:
-
int[26]表示字母 'a' - 'z' 或者 'A' - 'Z' -
int[128]表示 ASCII 字符集 -
int[256]表示 扩展ASCII 字符集
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
int[] index = new int[128]; // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
i = Math.max(index[s.charAt(j)], i);
ans = Math.max(ans, j - i + 1);
index[s.charAt(j)] = j + 1;
}
return ans;
}
}
复杂度分析
- 时间复杂度:O(n)。使用下标 j 循环了 n 次。
- 空间复杂度
Map:O(min(m,n))。与之前的解法相同。 - 空间复杂度
int[]:O(m)。m为字符集的大小。