幸存者预测??听起来是不是很有意思;没错!!更有意思的还在后面;本期给大家详细介绍如果通过随机森林算法预测泰坦尼克号幸存者的全过程;工具采用R语言,案例来自于Kaggle。
案例背景
泰坦尼克号沉船事故是世界上最著名的沉船事故之一。1912年4月15日,在她的处女航期间,泰坦尼克号撞上冰山后沉没,造成2224名乘客和机组人员中超过1502人的死亡。这一轰动的悲剧震惊了国际社会,并导致更好的船舶安全法规。
事故中导致死亡的一个原因是许多船员和乘客没有足够的救生艇。然而在被获救群体中也有一些比较幸运的因素;一些人群在事故中被救的几率高于其他人,比如妇女、儿童和上层阶级。
这个Case里,我们需要分析和判断出什么样的人更容易获救。最重要的是,要利用机器学习来预测出在这场灾难中哪些人会最终获救;
数据样本
点这里下载
数据挖掘流程
- 1 加载和检查数据
#加载包
library('ggplot2') #可视化
library('ggthemes') # 可视化
library('scales') # 可视化
library('dplyr') # 数据处理
library('mice') # 可视化
library('randomForest') # 分类算法
包安装好了,继续加载数据
setwd("A:\\...")
train <- read.table("train.csv",stringsAsFactors = F,header = T,sep=",",na.strings = "")
test <- read.table("test.csv",stringsAsFactors = F,header = T,sep=",",na.strings = "")
full <- bind_rows(train, test) # 将训练和测试集合并
查看下数据结构:
# check data
str(full)
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 1309 obs. of 12 variables:
$ PassengerId: int 1 2 3 4 5 6 7 8 9 10 ...
$ Survived : int 0 1 1 1 0 0 0 0 1 1 ...
$ Pclass : int 3 1 3 1 3 3 1 3 3 2 ...
$ Name : chr "Braund, Mr. Owen Harris" "Cumings, Mrs. John Bradley (Florence Briggs Thayer)" "Heikkinen, Miss. Laina" "Futrelle, Mrs. Jacques Heath (Lily May Peel)" ...
$ Sex : chr "male" "female" "female" "female" ...
$ Age : num 22 38 26 35 35 NA 54 2 27 14 ...
$ SibSp : int 1 1 0 1 0 0 0 3 0 1 ...
$ Parch : int 0 0 0 0 0 0 0 1 2 0 ...
$ Ticket : chr "A/5 21171" "PC 17599" "STON/O2. 3101282" "113803" ...
$ Fare : num 7.25 71.28 7.92 53.1 8.05 ...
$ Cabin : chr NA "C85" NA "C123" ...
$ Embarked : chr "S" "C" "S" "S" ...
以上,我们知道我们处理的样本拥有1309个观测值,每个观测值含有12个变量。为了更方便的理解样本,下面列出12个变量的释义:
Survived : 取值0和1,0表示死亡,1表示获救
Pclass :乘客的船仓等级
Name :乘客姓名
Sex :乘客性别
Age :乘客年龄
SibSp :船上配偶兄妹的人数
Parch :船上父母孩子的人数
Ticket :票号
Fare :票价
Cabin :乘客船舱号
Embarked :出发港口
- 2 特征工程
乘客姓名变量包含了许多信息,比如性别;另外还可以用姓氏来寻找一个家庭中的诸多成员。
#从乘客名称中提取头衔信息
full$Title <- gsub('(., )|(\..)', '', full$Name)
# 统计不同头衔中对应不同性别的人数
table(full$Sex, full$Title)
## Capt Col Don Dona Dr Jonkheer Lady MajorMasterMiss Mlle Mme
## female 0 0 0 1 1 0 1 0 0 260 2 1
## male 1 4 1 0 7 1 0 2 61 0 0 0
## Mr Mrs Ms Rev Sir the Countess
## female 0 197 2 0 0 1
## male 757 0 0 8 1 0
容易看到 Dona, Lady, the Countess,Capt, Col, Don, Dr, Major, Rev, Sir, Jonkheer 这些头衔出现的次数很少;而MIle,Mme,Ms都是女性,此处怀疑工作人员笔误将Miss写错MIle,Mme,将Mrs写成Ms;于是:
# 出现频次很低的头衔统一替换成'Rale Title'
rare_title <- c('Dona', 'Lady', 'the Countess','Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer')
# 将Mlle,Ms,Mme替换成Miss,Miss,Mrs
full$Title[full$Title == 'Mlle'] <- 'Miss'
full$Title[full$Title == 'Ms'] <- 'Miss'
full$Title[full$Title == 'Mme'] <- 'Mrs'
full$Title[full$Title %in% rare_title] <- 'Rare Title'
# 输出头衔和性别的交叉列联表
table(full$Sex, full$Title)
输出结果如下:
## Master Miss Mr Mrs Rare Title
## female 0 264 0 198 4
## male 61 0 757 0 25
最后,我们从用户全民中提取用户的姓氏
# 提取姓氏
namefull$Surname <- sapply(full$Name, function(x) strsplit(x, split = '[,.]')[[1]][1])
我们已经处理了用户的姓名;下面我们将创建一个家庭规模变量,以反映出用户有多少家庭成员在船上。
# 创建家庭规模变量
full$Fsize <- full$SibSp + full$Parch + 1# Create a family variable
full$Family <- paste(full$Surname, full$Fsize, sep='_')
用户的家庭规模能反映出什么呢?为了帮助大家理解家庭规模和是否被救之间有什么影响,我们用一张图来展示:
# 用ggplot2包画出家庭规模与用户被救之间的关系
ggplot(full[1:891,], aes(x = Fsize, fill = factor(Survived))) +
geom_bar(stat='count', position='dodge') +
scale_x_continuous(breaks=c(1:11)) +
labs(x = 'Family Size')
容易看到孤身一人和家庭规模大于4的用户中被救的人数偏少:家庭规模在2~4之间的用户被救的人数偏多。于是我们再建立一个表征家庭规模大小的变量FsizeD:
full$FsizeD[full$Fsize == 1] <- 'singleton'
full$FsizeD[full$Fsize < 5 & full$Fsize > 1] <- 'small'
full$FsizeD[full$Fsize > 4] <- 'large'
我们再通过马赛克图展现不同规模用户的获救概率:
- 3 缺失值处理
处理样本缺失值的方法有很多,但对于只有1300多个观测值的小样本而言,我们不会通过删除含有缺失值的观测值来处理缺失数据;我们可以用特定值(比如均值)来填补缺失值,也可以通过预测来填补缺失值;
首先我们发现第62和830位乘客缺失了出发港口的指标数据(Embarked)
full[c(62, 830), 'Embarked']
## Source: local data frame [2 x 1]
##
## Embarked
## (chr)
## 1
## 2
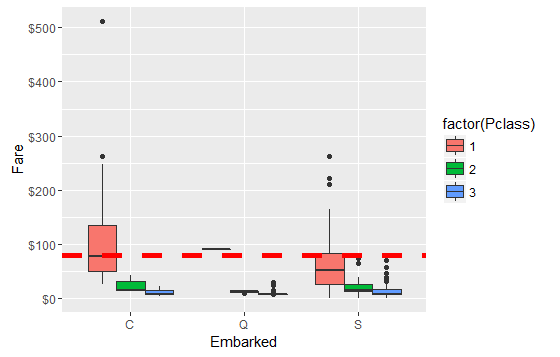
通过观察,62和830号乘客的票价均为80美元,而且船舱等级为一等舱;可以推测用户从哪个港口出发可能会影响不同等级船舱的票价;
# 先剔除62和830号乘客的信息
embark_fare <- full %>% filter(PassengerId != 62 & PassengerId != 830)
# 通过箱线图展示出发港口、船舱等级、票价三者关系
ggplot(embark_fare, aes(x = Embarked, y = Fare, fill = factor(Pclass))) +
geom_boxplot() +
geom_hline(aes(yintercept=80), colour='red', linetype='dashed', lwd=2) +
scale_y_continuous(labels=dollar_format())
从图上看出,票价在80美元而且船舱等级是一等舱的乘客只有可能从C地出发;因此第62和830号乘客的出发地是C。
full$Embarked[c(62, 830)] <- 'C'
第1044位乘客缺失了船票价格;
full[1044, ]
## Source: local data frame [1 x 18]
##
## PassengerId Survived Pclass Name Sex Age SibSp Parch
## (int) (int) (int) (chr) (chr) (dbl) (int) (int)
## 1 1044 NA 3 Storey, Mr. Thomas male 60.5 0 0
## Variables not shown: Ticket (chr), Fare (dbl), Cabin (chr), Embarked
## (chr), Title (chr), Surname (chr), Fsize (dbl), Family (chr), FsizeD
## (chr), Deck (fctr)
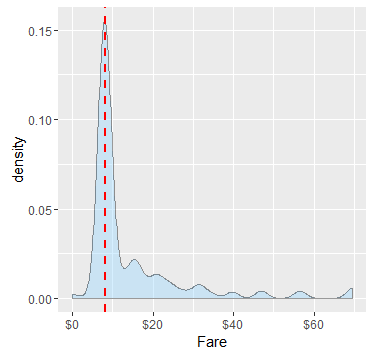
由于这位乘客从S港口出而且船舱等级是3级,所以我们看看从S港口出发且船舱等级是3级的所有乘客的票价是如何分布的:
#通过密度图展示不同票价的的分布趋势
ggplot(full[full$Pclass == '3' & full$Embarked == 'S', ],
aes(x = Fare)) +
geom_density(fill = '#99d6ff', alpha=0.4) +
geom_vline(aes(xintercept=median(Fare, na.rm=T)),
colour='red', linetype='dashed', lwd=1) +
scale_x_continuous(labels=dollar_format())
上图看出,我们用票价均值(红虚线)来替代1044号乘客缺失的票价数据是相对合理的;于是:
full$Fare[1044] <- median(full[full$Pclass == '3' & full$Embarked == 'S', ]$Fare, na.rm = TRUE)
以上我们简单处理了一些缺失数据,但是整个数据集中年龄字段仍有较多缺失值存在,因为年龄是数值型变量;所以我们可以结合其他的变量数据通过模型来预测出缺失数据。
# 统计缺失数据数量
sum(is.na(full$Age))
## [1] 263
这里我们采用常用的缺失值处理包mice。
# 将一些字符型输入变量转化成因子类型
factor_vars <- c('PassengerId','Pclass','Sex','Embarked', 'Title','Surname','Family','FsizeD')
# 设定随机数种子
seedset.seed(520)
#调用mice包,输入变量中剔除一些价值很低的变量
mice_mod <- mice(full[, !names(full) %in% c('PassengerId','Name','Ticket','Cabin','Family','Surname','Survived')], method='rf')
##
## iter imp variable
## 1 1 Age Deck
## 1 2 Age Deck
## 1 3 Age Deck
## 1 4 Age Deck
## 1 5 Age Deck
## 2 1 Age Deck
## 2 2 Age Deck
## 2 3 Age Deck
## 2 4 Age Deck
## 2 5 Age Deck
## 3 1 Age Deck
## 3 2 Age Deck
## 3 3 Age Deck
## 3 4 Age Deck
## 3 5 Age Deck
## 4 1 Age Deck
## 4 2 Age Deck
## 4 3 Age Deck
## 4 4 Age Deck
## 4 5 Age Deck
## 5 1 Age Deck
## 5 2 Age Deck
## 5 3 Age Deck
## 5 4 Age Deck
## 5 5 Age Deck
# 保存输出值
mice_output <- complete(mice_mod)
下面我们比较一下预测出的age分布和原始数据中的age分布有没有较大差异:
# 画出年龄密度分布图
par(mfrow=c(1,2))
hist(full$Age, freq=F, main='Age: Original Data', col='darkgreen', ylim=c(0,0.04))
hist(mice_output$Age, freq=F, main='Age: MICE Output', col='lightgreen', ylim=c(0,0.04))
非常好;预测前后的年龄分布并没有明显差异;下面将预测后的年龄数据替换到原始数据当中:
full$Age <- mice_output$Age
#统计新数据集中的缺失值数量
sum(is.na(full$Age))
## [1] 0
既然我们补全了age字段的缺失值数据,那么下面我们继续利用age字段做一些特征工程。例如我们可以通过age来大致确定哪些人是孩子、哪些人是母亲;孩子的age一般都是小于18的;而母亲这可能满足:1.age大于18;2.至少拥有一个孩子啊;3.全名中不带有Miss字符;4.性别是女性。
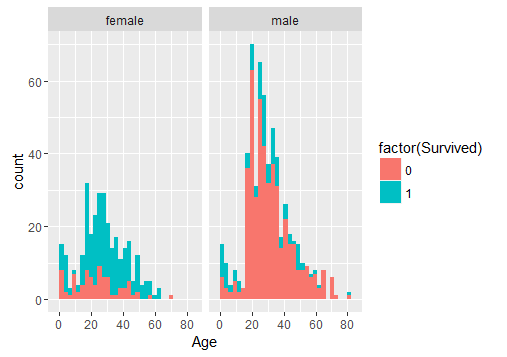
# 首选我们观察下不同性别当中年龄与是否被救之间的关系
ggplot(full[1:891,], aes(Age, fill = factor(Survived))) +
geom_histogram() +
# 性别对于预测有明显意义,因为我们预先知道女性获救的几率更大(这是一个先验概率)
facet_grid(.~Sex)
于是我们在样本集中新增加一列child:
full$Child[full$Age < 18] <- 'Child'
full$Child[full$Age >= 18] <- 'Adult'
# Show counts
table(full$Mother, full$Survived)
##
## 0 1
## Adult 484 274
## Child 65 68
数据上显示如果你是一个孩子,那么在这场灾难中你被救的概率约有1/2;下面我们继续创建新变量mother,我们期待能够在数据用印证母亲被救的可能性更大这一先验假设。
#增加mother变量
full$Mother[full$Sex == 'female' & full$Parch > 0 & full$Age > 18 & full$Title != 'Miss'] <- 'Mother'
table(full$Mother, full$Survived)
##
## 0 1
## Mother 16 39
## Not Mother 533 303
# 将child和mother变量转化成因子类型
full$Child <- factor(full$Child)
full$Mother <- factor(full$Mother)
到这里,我们完成了所有的数据处理工作。(** 是不是觉得超级枯燥、超级繁琐;没错!这就是数据分析的现实,80%的工作都集中在数据处理环节!**)
- 4 模型建立
预测环节中输入变量除了最开始数据集中包含的之外,我们还陆续添加了一些新的变量;比如child、mother、Fsize、FsizeD等;这里我们选用随机森林算法(RandomForest,关于随机森林算法)进行分类预测;
第一步,我们首先从原始样本full中剥离出训练集和测试集;
train <- full[1:891,]
test <- full[892:1309,]
第二步、带入训练集进行样本训练:
#设立随机数种子
set.seed(9999)
# 模型建立
rf_model <- randomForest(factor(Survived) ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked + Title + FsizeD + Child + Mother, data = train)
#展示模型误差(包含袋外误差、正例误差和负例误差)
plot(rf_model, ylim=c(0,0.36))legend('topright', colnames(rf_model$err.rate), col=1:3, fill=1:3)
黑线代表总体误差(oob袋外误差),保持在20%左右;
蓝线代表正例误差率(对被救概率的预测),保持在30%左右;
红线代表负例误差率(对死亡概率的预测),保持在10%左右;
因此,容易看出,该模型对负例的预测精度明显高于正例预测精度。
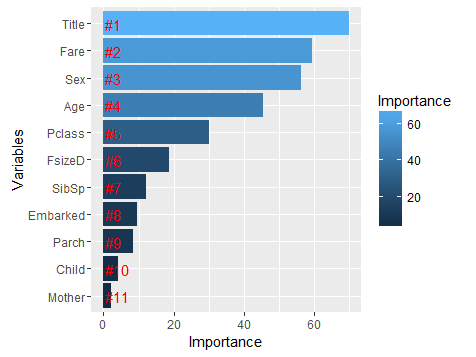
下面我们通过Gini系数来了解下模型的每个输入变量对模型的重要性程度有什么不同:
importance <- importance(rf_model)
varImportance <- data.frame(Variables = row.names(importance), Importance = round(importance[ ,'MeanDecreaseGini'],2))
rankImportance <- varImportance %>%
mutate(Rank = paste0('#',dense_rank(desc(Importance))))
# 作图
ggplot(rankImportance, aes(x = reorder(Variables, Importance), y = Importance, fill = Importance)) +
geom_bar(stat='identity') +
geom_text(aes(x = Variables, y = 0.5, label = Rank), hjust=0, vjust=0.55, size = 4, colour = 'red') + labs(x = 'Variables') +
coord_flip()
- 5 结果预测
# 将模型带入测试集
prediction <- predict(rf_model, test)
# 保存结果
solution <- data.frame(PassengerID = test$PassengerId, Survived = prediction)
# 输出结果到CSV文件格式
write.csv(solution, file = 'rf_mod_Solution.csv', row.names = F) - 6 结语
灾难预测是Kaggle上比较热门和基础的算法竞赛题目;这篇文章主要给大家展示一整套数据挖掘流程和机器学习算法建模实例以及如何将数据结果可视化展示;当然,如果你在该赛题中应用本文思路,提交结果可直接排名500+左右;文中的数据处理思路来自于Megan Risdal 。