机器学习的理论部分大致过了一遍了,下一步要理论联系实践了。Kaggle是一个很好的练手场,这个数据挖掘比赛平台最宝贵的资源有两个:
- 各种真实场景产生的数据集。这些数据集并不像著名的MNIST、CIFAR-10等数据集一样整齐和完整,它们当中有缺失值,有难以处理的特征,也有离群值和噪声,这更接近实际应用中的情况,可以锻炼我们数据预处理、数据清洗、特征工程的能力。
- 各路大牛在线分享经验,讨论从数据中发现的模式。这其实才是Kaggle最吸引人的地方,因为这些数据比赛并没有官方的最好答案,在这里一切以最后的score说话,很多高分team处理数据的方法是很值得学习的。
和多数小白一样,在面对Kaggle众多比赛无从下手的时候,我选择从最简单的Titanic预测生还者比赛入门。
1、数据清洗和预处理
数据的质量决定模型能达到的上界。这话说的无比正确。机器学习的算法模型是用来挖掘数据中潜在模式的,但若是数据太过杂乱,潜在的模式就很难找到,更糟的情况是,我们所收集的数据的特征和我们想预测的标签之间并没有太大关联,这时候这个特征就像噪音一样只会干扰我们的模型做出准确的预测。
综上所述,我们要对拿到手的数据集进行分析,并看看各个特征到底会不会显著影响到我们要预测的标签值。
首先我们导入机器学习和数据挖掘中最常用也最强大的几个库——numpy、pandas、matplotlib。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
第一步是使用pd.read_csv()方法导入数据:
train = pd.read_csv(r'C:\Users\Sidney Nash\Desktop\data\train.csv')
test = pd.read_csv(r'C:\Users\Sidney Nash\Desktop\data\test.csv')
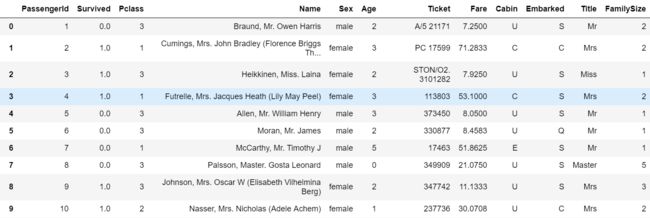
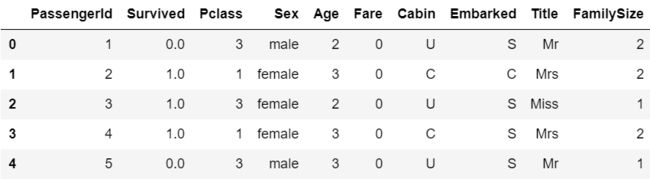
第二步是展示数据和观察数据(由于数据量大,一般用head()展示前五行):
train.head()
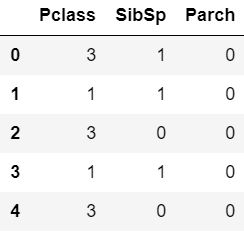
可以看到,每个乘客有12个属性,其中PassengerId在这里只起到索引作用,而Survived是我们要预测的目标,因此实际上我们需要处理的特征一共有10个,因此我们可以先去掉PassengerId和Survived,并对余下特征进行观察:
drop_features=['PassengerId','Survived']
train_drop=train.drop(drop_features,axis=1)
train_drop.head()
我们看到,这些特征的类型各不相同,有整数型的、浮点数型的,也有字符型的,我们先审视一下各特征的类型:
train_drop.dtypes.sort_values()
out:
Pclass int64
SibSp int64
Parch int64
Age float64
Fare float64
Name object
Sex object
Ticket object
Cabin object
Embarked object
dtype: object
然后按把同类型的放在一起:
train_drop.select_dtypes(include='int64').head()
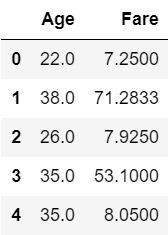
train_drop.select_dtypes(include='float64').head()
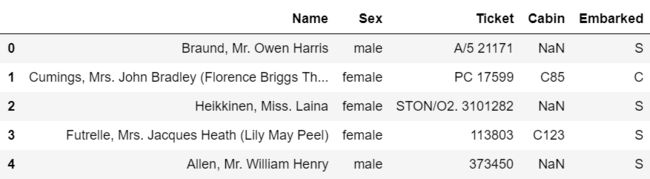
train_drop.select_dtypes(include='object').head()
知道了各类型的特征都有哪些,下一步我们要看看特征中是否有缺失值:
train.isnull().sum()[lambda x: x>0]
out:
Age 177
Cabin 687
Embarked 2
dtype: int64
可以看到,Age和Cabin两个特征的缺失值数量较多,于是我们接下来重点关注这两个特征的缺失值补全就行了,是这样吗?NoNoNo,这只是训练集train,我们不能想当然地认为test中的情形和train相同,我们看一下test中的情况:
test.isnull().sum()[lambda x: x>0]
out:
Age 86
Fare 1
Cabin 327
dtype: int64
果然还是有些差别的,虽然差别很微小,但依然可能对模型结果产生影响。
实际上,pandas中有更为方便的方法来列出缺失值以及各特征的一些统计信息,那就是info()和describe():
train.info()
out:
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
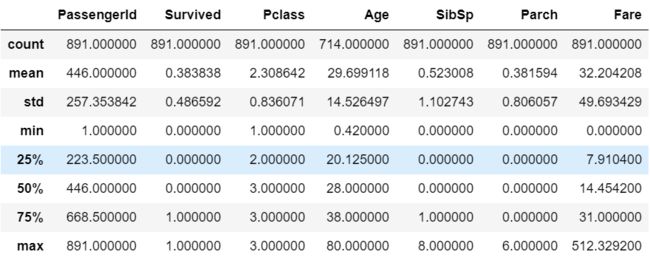
train.describe()
当然这里我们只列出了train的统计信息,对test也是同理。进行到这里,我们发现每次都对train和test进行同样的操作很麻烦,后续我们添加新特征或删改原特征的时候更是如此,为什么不把train和test合并起来统一操作呢?下面我们把两者合并(注意,合并的时候不能让各个记录重新排序,否则我们难以再将train和test拆分开来):
titanic=pd.concat([train, test], sort=False)
#这里记录train中的记录个数是为了后面将train和test拆分开来
len_train=train.shape[0]
现在我们查看合并后的titanic的信息:
titanic.info()
out:
Int64Index: 1309 entries, 0 to 417
Data columns (total 12 columns):
PassengerId 1309 non-null int64
Survived 891 non-null float64
Pclass 1309 non-null int64
Name 1309 non-null object
Sex 1309 non-null object
Age 1046 non-null float64
SibSp 1309 non-null int64
Parch 1309 non-null int64
Ticket 1309 non-null object
Fare 1308 non-null float64
Cabin 295 non-null object
Embarked 1307 non-null object
dtypes: float64(3), int64(4), object(5)
memory usage: 132.9+ KB
len_train==891
out:
True
我们可以看到Age、Fare、Cabin和Embarked四个特征均有缺失值(注意这里的Survived并没有缺失值,因为只有train有标签Survived,test的Survived是我们的训练目标)。
处理缺失值一般有两种方式,第一种就是舍弃包含较多缺失值的特征,这个做法对我们这个小规模的数据集来说不太适用,因为我们本来掌握的信息就不多,若再舍弃一些信息,可能会造成模型效果不佳。第二种是进行缺失值补全,一般根据实际情况将缺失值补全为0、特征列均值或中位数,或者将缺失值划入一个新的类别特殊处理。
在进行特征值补全之前,我们先处理一个虽然没有缺失值但很难利用的特征——Name。
每个人的名字都是独一无二的,名字和幸存与否看起来并没有直接关联,那怎么利用这个特征呢?有用的信息其实隐藏在称呼当中,比如我们猜测上救生艇的时候是女士优先,那么称呼为Mrs和Miss的就比称呼为Mr的更可能幸存。于是我们从Name特征中其称呼并建立新特征列Title。
titanic['Title'] = titanic.Name.apply(lambda name: name.split(',')[1].split('.')[0].strip())
看一下效果:
titanic.head()
ok,我们已经把称呼提取出来了,下面我们来看看称呼的种类和数量:
titanic.Title.value_counts()
out:
Mr 757
Miss 260
Mrs 197
Master 61
Rev 8
Dr 8
Col 4
Mlle 2
Ms 2
Major 2
Capt 1
Lady 1
Jonkheer 1
Don 1
Dona 1
the Countess 1
Mme 1
Sir 1
Name: Title, dtype: int64
emmm,大类似乎只有四个:Mr、Miss、Mrs、Master,其余称呼非常少,因此我们将其余称呼都归为一类——Rare。
List=titanic.Title.value_counts().index[4:].tolist()
mapping={}
for s in List:
mapping[s]='Rare'
titanic['Title']=titanic['Title'].map(lambda x: mapping[x] if x in mapping else x)
titanic.Title.value_counts()
out:
Mr 757
Miss 260
Mrs 197
Master 61
Rare 34
Name: Title, dtype: int64
这样我们就把称呼划分成了5大类,下一步我们可以根据称呼来对Age的缺失值进行补全了,这是因为Miss用于未婚女子,通常其年龄比较小,Mrs则表示太太,夫人,一般年龄较大,因此利用称呼中隐含的信息去推测其年龄是合理的。下面我们根据Title进行分组并对Age进行补全。
grouped=titanic.groupby(['Title'])
median=grouped.Age.median()
median
out:
Title
Master 4.0
Miss 22.0
Mr 29.0
Mrs 35.5
Rare 44.5
Name: Age, dtype: float64
可以看到,不同称呼的乘客其年龄的中位数有显著差异,因此我们只需要按称呼对缺失值进行补全即可,这里使用中位数(平均数也是可以的,在这个问题当中两者差异不大,而中位数看起来更整洁一些)。
def newage (cols):
age=cols[0]
title=cols[1]
if pd.isnull(age):
return median[title]
return age
titanic.Age=titanic[['Age','Title']].apply(newage,axis=1)
titanic.info()
out:
Int64Index: 1309 entries, 0 to 417
Data columns (total 13 columns):
PassengerId 1309 non-null int64
Survived 891 non-null float64
Pclass 1309 non-null int64
Name 1309 non-null object
Sex 1309 non-null object
Age 1309 non-null float64
SibSp 1309 non-null int64
Parch 1309 non-null int64
Ticket 1309 non-null object
Fare 1308 non-null float64
Cabin 295 non-null object
Embarked 1307 non-null object
Title 1309 non-null object
dtypes: float64(3), int64(4), object(6)
memory usage: 183.2+ KB
可以看到,Age的缺失值已经被我们补全了。下面我们对Cabin、Embarked以及Fare进行补全。
首先Cabin代表的是舱位号,这个信息似乎并不能由其它的特征推出来(我本来想着ticket这个特征会有些帮助,但是我发现这个船票号似乎并没有什么规律),那么我们可以想一想为什么舱位号的缺失值这么多呢?会不会是因为只有幸存者才能准确地登记自己的舱位号呢?也就是说,会不会舱位号的有无才是关键所在呢?为了验证这个想法,我们画出幸存与舱位的关系图(注意这里只能画出train中has_Cabin和Survived的关系):
titanic['has_Cabin'].loc[~titanic.Cabin.isnull()]=1
titanic['has_Cabin'].loc[titanic.Cabin.isnull()]=0
pd.crosstab(titanic.has_Cabin[:len_train],train.Survived).plot.bar(stacked=True)
不难看出,舱位号缺失的乘客的幸存率远远低于有舱位号的乘客,这就验证了我之前的猜想。于是我们把Cabin的缺失值划为单独的一类。
titanic.Cabin = titanic.Cabin.fillna('U')
titanic[:10]
然后我们看Embarked特征,这个特征表示在那个港口登船,只有两个缺失值,对结果影响不大,所以直接把缺失值补全为登船港口人数最多的港口(这其实应用的是先验概率最大原则)。
most_embarked = titanic.Embarked.value_counts().index[0]
titanic.Embarked=titanic.Embarked.fillna(most_embarked)
最后我们补全Fare,这个只有一个缺失值,对结果影响不大,所以直接用票价Fare的中位数补全。
titanic.Fare = titanic.Fare.fillna(titanic.Fare.median())
至此我们的缺失值补全就完成了,check一下:
titanic.info()
out:
Int64Index: 1309 entries, 0 to 417
Data columns (total 13 columns):
PassengerId 1309 non-null int64
Survived 891 non-null float64
Pclass 1309 non-null int64
Name 1309 non-null object
Sex 1309 non-null object
Age 1309 non-null float64
SibSp 1309 non-null int64
Parch 1309 non-null int64
Ticket 1309 non-null object
Fare 1309 non-null float64
Cabin 1309 non-null object
Embarked 1309 non-null object
Title 1309 non-null object
dtypes: float64(3), int64(4), object(6)
memory usage: 183.2+ KB
ok,下一步我们进行特征工程对补全后的特征做进一步处理。
2、特征工程
首先我们处理Cabin特征,原因很简单,因为它的形式比较复杂(字母加数字),不方便直接使用。
我们猜测Cabin特征中的开头字母应该是舱位等级,于是我们把Cabin特征中的数字去掉以方便分析:
titanic['Cabin'] = titanic.Cabin.apply(lambda cabin: cabin[0])
titanic.Cabin.value_counts()
out:
U 1014
C 94
B 65
D 46
E 41
A 22
F 21
G 5
T 1
舱位等级A~G没有问题,但是T是什么舱呢……我个人感觉这个应该是登记错误吧,看了眼票价并不是很贵,于是手动把它标记成G好了……
titanic['Cabin'].loc[titanic.Cabin=='T']='G'
titanic.Cabin.value_counts()
out:
U 1014
C 94
B 65
D 46
E 41
A 22
F 21
G 6
Name: Cabin, dtype: int64
我们现在看看这样划分是否对预测有用。
pd.crosstab(titanic.Cabin[:len_train],train.Survived).plot.bar(stacked=True)
看起来似乎A~F的幸存率都不低,不过各舱位之间还是有差别的。
接下来我们对其它特征进行筛选或组合,标准就是和幸存率相关性大。
我们先看Parch(直系亲人)和SibSp(旁系亲人)两个特征。
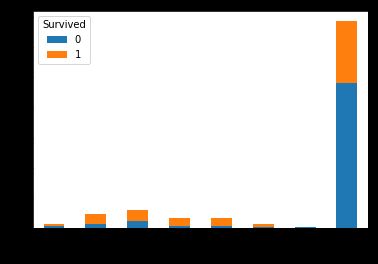
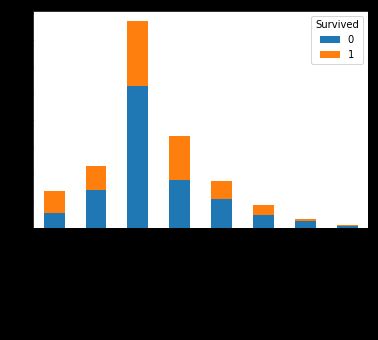
pd.crosstab(titanic.Parch[:len_train],train.Survived).plot.bar(stacked=True)
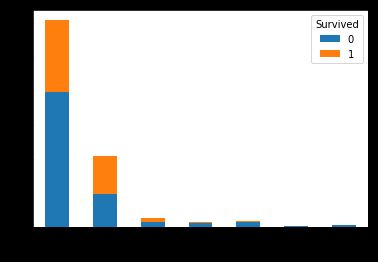
pd.crosstab(titanic.SibSp[:len_train],train.Survived).plot.bar(stacked=True)
看起来这两个特征对幸存率的影响差不多啊……那我们把这两个特征整合成一个特征好了,Parch+SibSp+1就是家庭大小,我们创建新特征FamilySize。
titanic['FamilySize'] = titanic.Parch + titanic.SibSp + 1
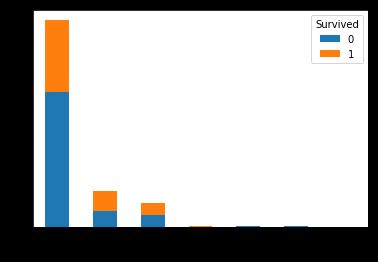
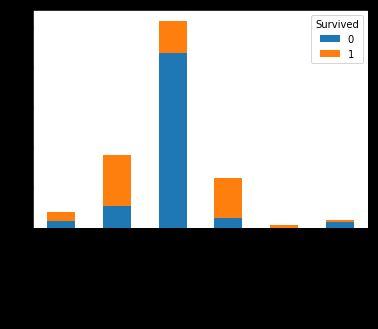
pd.crosstab(titanic.FamilySize[:len_train],train.Survived).plot.bar(stacked=True)
可以看到,孤身一人的死亡率极高……两口之家三口之家和四口之家的存活概率都比较高,家庭规模再大一些的死亡率又有所回升,这个结果也在情理之中。
于是我们添加FamilySize这个特征,并去掉SibSp和Parch两个特征。
titanic=titanic.drop(['SibSp','Parch'],axis=1)
接下来我们看Sex特征。
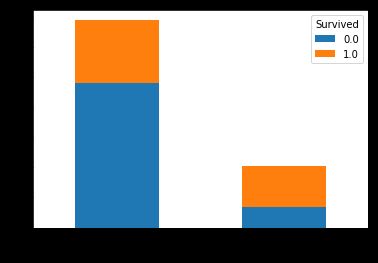
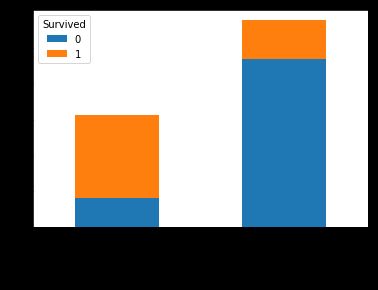
pd.crosstab(titanic.Sex[:len_train],train.Survived).plot.bar(stacked=True)
女性的幸存率比男性要大很多,看来lady first的绅士风度并不只是说说而已。
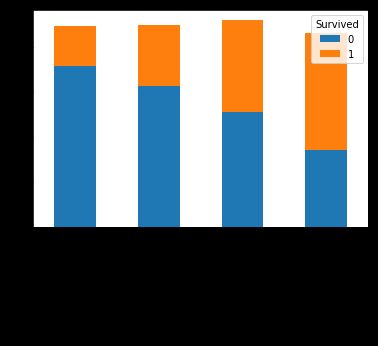
接下来我们看Pclass特征。
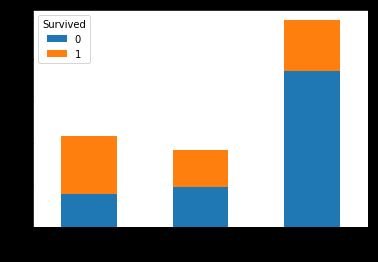
pd.crosstab(titanic.Pclass[:len_train],train.Survived).plot.bar(stacked=True)
不出所料,阶级高的人存活率要远大于阶级低的人。
接下来是Title。
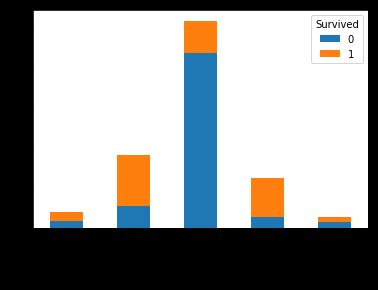
pd.crosstab(titanic.Title[:len_train],train.Survived).plot.bar(stacked=True)
直观上看,这个特征其实和Sex包含的信息差不多啊,都是男性幸存率低女性幸存率高。那么它还包含更多有用信息吗,我们把Sex和Title组合起来看看。
pd.crosstab([titanic.Title[:len_train],titanic.Sex[:len_train]],train.Survived).plot.bar(stacked=True)
可以看到,相比Sex,Title确实提供了更多信息,比如虽然男性的幸存率低,但是男孩(Master)的幸存率却达到了将近50%。而Title在Sex的补充下也呈现出新的信息,比如虽然Rare的幸存率虽然并不太高,但Rare中的女性幸存率却很高。
综上,我们要保留Title特征。
那么Age特征呢?首先将其当作连续特征是不好处理的,所以我们应划分年龄段来观察:
pd.crosstab(pd.cut(titanic.Age,8)[:len_train],train.Survived).plot.bar(stacked=True)
看起来只有年龄很小的孩子受到了优待,年轻人死亡率最高,而年纪稍长者存活率较高,老者存活率最低。
我们按照年龄段将Age转化为类别特征:
titanic.Age=pd.cut(titanic.Age,8,labels=False)
接下来看Embarked特征。
pd.crosstab(titanic.Embarked[:len_train],train.Survived).plot.bar(stacked=True)
可以看到C港口上船的乘客幸存率最高,其它两个港口幸存率较低。原因不详。
目前为止,我们得到的特征长这样:
我们看到,形式比较复杂的特征还有Name、Ticket和Fare三个,Name的信息我们认为已经被Title涵盖了,因此直接舍弃。
titanic=titanic.drop('Name',axis=1)
Ticket我不知道其中含义,而且我认为其中的重要信息应该已经包含在Cabin当中了,于是我选择舍弃Ticket这个特征。
titanic=titanic.drop('Ticket',axis=1)
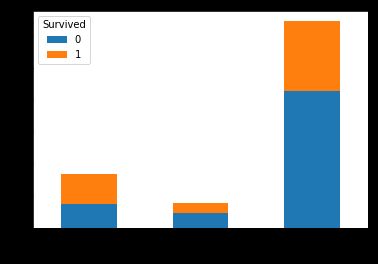
最后,我们看Fare特征,我个人认为这个船票价格并不太重要,因为其信息应该已经包含在Pclass、Cabin以及Embarked当中了,但我猜想这个票价可能和位置有关(靠窗啊卧铺啊之类),蕴含了我们舍弃的Ticket的部分信息,因此我决定保留这个特征,并对其进行和Age类似的离散化操作。
pd.crosstab(pd.qcut(titanic.Fare,4)[:len_train],train.Survived).plot.bar(stacked=True)
果然票价越高幸存率越高。
我们按照Fare段将Fare转化为类别特征:
titanic.Fare=pd.cut(titanic.Fare,4,labels=False)
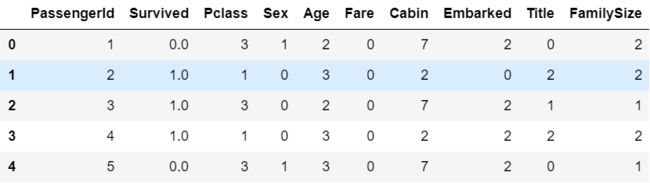
我们看一下现在的特征形式:
titanic.head()
基本上完成了,最后我们只需把Sex、Cabin、Embarked和Title特征转化成int类型即可:
titanic.Sex=titanic.Sex.map({'male':1,'female':0})
titanic.Cabin=titanic.Cabin.map({'A':0,'B':1,'C':2,'D':3,'E':4,'F':5,'G':6,'U':7})
titanic.Embarked=titanic.Embarked.map({'C':0,'Q':1,'S':2})
titanic.Title=titanic.Title.map({'Mr':0,'Miss':1,'Mrs':2,'Master':3,'Rare':4})
至此特征工程就完成了:
3、训练模型
训练模型阶段我们只需要用sklearn库即可完成大部分操作,因为不知道何种模型是最适合我们的数据的,因此我们可以尝试多种模型,最终选出表现较好的模型进行集成,得到最终的分类器。
首先我们还原train和test数据。
train=titanic[:len_train]
test=titanic[len_train:]
然后我们可以给由这两个数据集产生相应的X和y了:
X_train=train.loc[:, 'Pclass':]
y_train=train['Survived']
X_test=test.loc[:, 'Pclass':]
然后我们尝试一下不同的模型,看看哪个效果比较好,这里考虑LR、SVM和DecisionTree。
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
log_reg=LogisticRegression()
log_reg.fit(X_train, y_train)
svm_clf = SVC()
svm_clf.fit(X_train, y_train)
tree_clf=DecisionTreeClassifier()
tree_clf.fit(X_train, y_train)
print(log_reg.score(X_train,y_train))
print(svm_clf.score(X_train,y_train))
print(tree_clf.score(X_train,y_train))
out:
0.8181818181818182
0.8462401795735129
0.8933782267115601
可以看到决策树模型表现更好一些,而决策树的集成是随机森林,因此我们直接使用随机森林来拟合数据。
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
RF=RandomForestClassifier(random_state=1)
PRF=[{'n_estimators':[10,100],'max_depth':[3,6],'criterion':['gini','entropy']}]
GSRF=GridSearchCV(estimator=RF, param_grid=PRF, scoring='accuracy',cv=2)
scores_rf=cross_val_score(GSRF,X_train,y_train,scoring='accuracy',cv=5)
model=GSRF.fit(X_train, y_train)
pred=model.predict(X_test)
output=pd.DataFrame({'PassengerId':test['PassengerId'],'Survived':pred})
output.to_csv('C:/logfile/submission.csv', index=False)
最终提交得分为0.7945,top 21%。对于入门之战来说结果已经不错了。后来又参考了网上大牛的做法,相比上面的模型,将Age的缺失值补全分得更为细致了一些(结合Title和Sex的信息进行补全而不仅仅是Title),并且采用了超参数调优的SVM模型,最终达到了0.8133的得分,排名瞬间变成top 7%。看来有很多人都卡在了0.8左右的精度上。