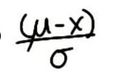之前已经看到了用直方图来显示数据集的重要性,以便分析图表形状,我们想要分析该形状,这样就可以严谨地思考平均值、中位数和众数并描述数据集,在偏态分布中平均值、中位数和众数各不相同,在很多情况下,中位数可能比平均值更有用,在正态分布中,平均值、中位数和众数几乎相等,还需要了解分布形状的哪些方面?
举例说明
我们用一个故事来讲解,我从小到大都在玩象棋,四岁就学会了,在 7 岁的时候就开始参加比赛,对于我的象棋能力,我可以说出三个方面,首先是我的象棋评分是 1800 分,所有竞争对手都有评分,其次是在参加比赛的美国
象棋选手中,我的排名是第 8,110 位,这是基于评分的, 第三,我的排名比 88% 的美国象棋选手都高,哪个可以让你清晰地了解到我的象棋水平? A.□ 我的象棋评分是 1800 分 B.□ 在参加比赛的美国象棋选手中,我的排名是第 8,110 位 C.□ 我的排名高于 88% 的美国象棋选手
C 对于A选项,对于大多数人来说,当我告诉他们我的评分是 1800 分时,他们并不知道这是什么意思,因为我们不知道评分范围是多少,最低分是多少,最高分是多少,有多少人得分大约为 1800 分,有多少人得分为 1,000 分,单凭这一个数据,信息量并不大。 对于B选项的数值也一样 我们大概知道有 8,000 人可能比我厉害,但是有多少人玩象棋呢? 百分比信息量就很大了,因此与找出平均值、中位数或众数哪个是最佳衡量指标相比,分布图的形状更加重要
在这之后我们关心的是数据值的比例,小于或大于数据集中的某个值,如果我告诉你我的评分是 1800 分,在我告诉你评分分布图的形状之前,你并不知道 1800 分的含义,你可以看到低于某个值的比例。
如果我们关心的是低于某个值的比例,我们应该如何对柱状图进行操作,使用绝对频率还是相对频率?
答案是使用相对频率,并将所有绝对频率转换为比例。
我们再来看一个示例
平均下来,人们有 190 个 Facebook 好友,假设他们的样本分布图是下图这样的,首先,将每个频率转换为相对频率,并绘制出相对频率图表,请点击每个条形高度对应的单选按钮,转换为比例
可以看到,相对频率分布图几乎和绝对频率分布图一样。
根据刚刚绘制的相对频率分布图,看看 Facebook 好友在 170 和 210 个之间所占的比例是多少?
如果看看该直方图,会发现中间两个最高的条形位于 170 和 210 之间,比例分别是 0.237 和 0.223,如果相加的话,结果是 0.46
上一个问题相对比较简单,但在现实生活中,很难回答我们要回答的问题,例如在 180 和 200 之间的比例是多少?
你可能已经看到 180 和 200 都位于分组中间,因此,我们无法确定这两个数字之间的比例是多少
注意,在之前提到了直方图存在的问题,为了方便牺牲了一些细节,由于这些分组,我们无法判断小于或大于某些数字的比例是多少?但是我们想知道这些信息,看看分布图中的某些得分与其他得分相比的结果,如何获得更多细节呢?向数据集中添加更多数据、增加组距还是减小组距?
更小的组距可以提供更多细节,例如,将组距减少一半,现在组距是 10 而不是 20,这样柱或区间的数量就翻了一番,现在多了一倍的数值,可以让我们清晰地知道大于或小于这些值的比例。
但是我们依然不知道有多少值小于每个分组之间的任何数值,例如,我们无法判断小于 175 的比例,理想情况下,我们尽量希望组距越小越好,实际上,是无穷小,但是随着我们增加分组数量足够大时,我们可以看到每个容器的频率要么是 0 或 1,这是因为分组太小了,很多分组中只有 1 个值甚至没有任何值,最终如果继续降低容器大小,分布图的形状变得松散起来
现在我们陷入了困境,我们想要很小的组距,尽量提供更多的细节信息,描述出数据值相对于分布图剩余数据值的位置,最终,我们开始丢失分布图的形状。如果组距很大,则无法判断小于任何数据值的比例,我们将使用一个分布图理论模型来解决这一难题,该模型的曲线比较光滑,使用的是相对频率,这是一个理论上连续的分布图,可以用方程式来表示,这个简单的功能即方程式,使我们能够计算 x 轴上任何两个值之间的比例,这个曲线下的面积是多少?这是个非常难的问题,注意,对于这个柱状图,所有相对频率的和是多少?
该曲线下的面积是 1,注意,对于频率来说,所有频率相加是 1 与之类似,该曲线下的面积等于所有容器里的所有频率的和,应该等于 1。
在大部分情况下,我们将重点研究正态分布数据,正态分布类型多样,有宽扁型、瘦高型或者介于二者之间,但曲线下的面积始终为 1 或 100%,之前还在正态分布数据集中看到平均值、中位数和众数几乎相等,在理论模型中,它们是完全相等的,理论模型是完美对称的,在现实生活中几乎不会发生,这些模型接近于我们的现实分布图,但是通常可以非常相近,在理论模型中,大多数数据都位于中间,分布在平均值、中位数和众数周围,之前我们有提到大约 68% 的数据在平均值的 1 个标准偏差内,95% 的数据在平均值的 2 个标准偏差内。
特定值在 x 轴上的位置通常用标准偏差来描述,如上图,A点是平均值,B点是平均值加 1 个标准偏差,C点是平均值加 2 个标准偏差,类似地,D点是平均值减 1 个标准偏差,E点是平均值减 2 个标准偏差,无论数值是多少,我们都可以将其转换为与平均值的标准偏差值,我们将其称为 Z值。
通过将正态分布中的数值转换为这个特殊数字 z就可以知道小于或大于该值的百分比,例如如果某个值与平均值相差 1 个标准偏差,则无论是哪种正态分布,我们都知道大约 84% 的数值小于该值,在之后, 我们将学习如何计算正态分布中小于或大于某个值的比例,在什么样的示例中,我们想要知道小于或大于特定值的比例呢?我们用另一个故事来描述
Andy:Katie,我一点也不受欢迎 Katie:别担心,我也是,我只有 63 个 Facebook 好友 Andy:我只有 54 个 Twitter 关注者 Facebook 好友的平均数量是 190 人 ,Twitter 关注者的平均数值是 208 人,看看比例,Katie的 Facebook 好友数是平均值的 33%,Andy的 Twitter 关注者也只有平均值的 25%
了解受欢迎程度更好的方式是看看分布情况,Facebook 好友和 Twitter 关注者的分布是正态的,Twitter 关注者的标准偏差是 60,但是 Facebook 好友的标准偏差只有 35,与平均值的标准偏差肯定是了解受欢迎程度
的更佳方式
根据这些分布情况 Katie的 Facebook 好友数量与Facebook 好友数量平均值的标准偏差是多少?注意,Katie有 63 个 Facebook 好友 Facebook 好友的平均数量是 190 个,标准偏差是 36,所以Katie的标准偏差是
多少?
Katie与平均值的偏差是 127,用 127 除以 36将得出标准偏差,也就是 63 与平均值的差值,结果等于 3.53,所以对于Katie所具有的好友数量,Katie低于平均值 3.53 个标准偏差。
相同的方法可以计算出Andy 大约低于平均值 2.57 个标准偏差
如果 Andy 只使用 Twitter 而Katie只使用 Facebook,可以说 Andy 没有Katie受欢迎吗?在这个简单示例中,注意我们对受欢迎程度的定义是 Facebook 好友或 Twitter 关注者的数量,是或否?为什么?
否,我们不能据此判断 Andy 更不受欢迎,即使他的Twitter 关注者比Katie的 Facebook 好友数量少,因为看分布图的话,它们都是不同的,我们可以通过在同一坐标轴上对比它们,换句话说,根据它们的唯一标准偏差,这叫做标准化分布图,使用 0 作为参考点。
当我们对 Andy 的数据和Katie的进行标准化后,发现Katie离平均值更远,标准化数据显示了在该分布图中的数值更高或更低,在 Facebook 好友分布图中,比Katie好友数多的人所占的比例比在 Twitter 关注者分布图中比 Andy 的关注者多的人所占的比例要高,也就是说Katie更不受欢迎。
标准偏差数量的公式:
我们不仅关心各个值与平均值之间的距离,还关心这些值是小于还是大于平均值,在 x 轴上标准化任何数值时我们得出 Z 值,之前就将其称为 Z值,我们始终会用 x 减去平均值,然后除以标准偏差,这样,当某个值小于平均值时,结果会是负的 z 值。z 值是指任何值距离平均值的标准偏差数。因此,我们可以将正态分布中的任何值转换为 z 值,这么转换时,我们就标准化了分布图,我们可以对任何正态分布图进行标准化。
我们来计算一下Katie的Z值是多少,Katie有 63 个 Facebook 好友,实际的 Facebook 好友数平均值是190,假设标准偏差是 36,则Katie的Z值是多少?
-3.53
负的 Z 值意味着什么? A.□ 原始值是负数 B.□ 原始值小于平均值 C.□ 原始值小于 0 D.□ 原始值减去均值是负数
BD
现在再做一道测验题,如果我们通过将所有值都转换为 z 值,来归一化分布图,该归一化分布图的新平均值会是多少?提示下,想想我们是怎么计算 z 值的,即该坐标轴上的任何值减去平均值,然后除以标准偏差。
注意,我们将下面这个分布图一直往这边移动,并移到 0 的位置,因为我们要减去平均值,所以本质上,如果我们有个平均值为 100 的正态分布图,我们减去平均值,即将该分布图往左移了 100 个位置,那么 新的平均值则为 0,
还有一个更难的概念性问题,在归一化该分布图后,该分布图的新标准偏差是多少?
注意,当我们计算分布图中任何值的 z 值时,首先减去平均值,这会平移分布图而不会改变分布图的形状,这样 0 就变成了平均值,然后除以标准偏差,这样就改变了形状。这么来理解,这是任意的分布图 这是平均值 μ 这是标准偏差 σ,表示 σ 距离平均值一个标准偏差,在标准化该分布图后 σ 的 z 值是多少?当我们减去 μ 时,我们将分布图平移了,使 μ 变成 0,所以 σ 的 z 值将是 (σ-0)/σ即 σ/σ=1,所以任何值的 z 值,即距离平均值一个标准偏差,在标准化分布图后将为 1,表示这个正态分布或标准分布的新标准偏差是 1。
总结下,对于任何正态分布,我们都可以通过以下方式归一化该分布:首先减去平均值,将其平移到 0 处,然后除以标准偏差,使标准偏差等于 1,这就叫做标准正态分布。平均值为 0,标准偏差为 1,所以D处的 z 值将为 -1,C是距离 2 个标准偏差,E是距离 -2 个标准偏差,现在,数据集中的每个值都用距离平均值的标准偏差来表示。
假设 Chris 非常受欢迎,他拥有的 Facebook 好友数大于平均值2.5 个标准偏差,也就是说他比 99% 的人好友数都要多,如果原始数据的真实标准偏差依然是 36,原始平均值依然是 190,那么,Chris有多少个
Facebook 好友?这次 我们将 z 值转换成实际的值,而不是将某个值转换成了对应的 z 值。
280 这是 Chris 的数据 比大约 99% 的人好友数都要多,高于平均值 2.5 个标准偏差,如果标准偏差是 36,那么 2.5 个标准偏差是多少?2.5 个标准偏差等于 36X2.5=90,所以 Chris 的好友数比平均值多 90 个,平均值是 190,190+90=280 所以 Chris 有 280 个 Facebook 好友。 另一种解答方法是使用方程式,Chris 的 z 值是 2.5,等于原始值减去平均值,然后除以标准偏差,如果代入已知的值 2.5 是 z 的值 x (他的 Facebook 好友数),减去平均值,然后除以标准偏差,如果按照代数方法,交叉相乘 然后加上 190 就得出了Chris 的好友数(用 x 表示)为 280。
,