- C++ 设计模式:抽象工厂(Abstract Factory)
冀晓武
C++设计模式c++设计模式抽象工厂模式
链接:C++设计模式链接:C++设计模式-工厂方法链接:C++设计模式-原型模式链接:C++设计模式-建造者模式抽象工厂(AbstractFactory)是一种创建型设计模式,它提供一个接口,用于创建一系列相关或相互依赖的对象,而无需指定它们的具体类。抽象工厂模式通常用于创建一组相关的产品对象,例如不同类型的机器人和它们的配件。1.问题分析在某些情况下,我们需要创建一组相关或相互依赖的对象,但我们
- 配音助手:自媒体神器,内置海量音色的语音,支持多主播配音
阿幸软件杂货间
媒体
软件介绍内置文字转语音,提供多个主播音色,男声、女声、小孩、方言。支持的场景也是比较多,比如:广告促销、有声读物、广播配音、影视配音、Ai配音等。这个软件是免费的,只不过需要通过手机号码登录就可以使用全部功能了。软件下载夸克下载
- Redis Sentinel(哨兵) 和 Redis Cluster(集群)
G丶AEOM
八股普通学习区Redisredis数据库缓存
哨兵机制和集群有什么区别Redis集群主要有两种,一种是RedisSentinel哨兵集群,一种是RedisCluster。主从集群,包括一个Master和多个Slave节点,Master负责数据的读写,Slave负责数据的读取,Master上收到的数据变更会同步到Slave节点上实现数据同步,但不提供容错和恢复,在Master宕机时不会选出新的Master,导致后续客户端所有写请求直接失败。所以
- CentOS7环境卸载MySQL5.7
Hadoop_Liang
mysql数据库mysql
备份重要数据切记,卸载之前先备份mysql重要的数据。备份一个数据库例如:备份名为mydatabase的数据库到backup.sql的文件中mysqldump-uroot-ppassword123mydatabase>backup.sql备份所有数据库mysqldump-uroot-ppassword123--all-databases>all_databases_backup.sql注意:-p后
- php SPOF
贵哥的编程之路(热爱分享 为后来者)
PHP语言经典程序100题php开发语言
1.什么是单点故障(SPOF)?单点故障指的是系统中某个组件一旦失效,整个系统或服务就会不可用。常见的单点有:数据库、缓存、Web服务器、负载均衡、网络设备等。2.常见单点故障场景只有一台数据库服务器,宕机后所有业务不可用只有一台Redis缓存,挂掉后缓存全部失效只有一台Web服务器,挂掉后网站无法访问只有一个负载均衡节点,挂掉后流量无法分发只有一条网络链路,断开后所有服务失联3.消除单点故障的主
- 霍夫变换(Hough Transform)算法原来详解和纯C++代码实现以及OpenCV中的使用示例
点云SLAM
算法图形图像处理算法opencv图像处理与计算机视觉算法直线提取检测目标检测霍夫变换算法
霍夫变换(HoughTransform)是一种经典的图像处理与计算机视觉算法,广泛用于检测图像中的几何形状,例如直线、圆、椭圆等。其核心思想是将图像空间中的“点”映射到参数空间中的“曲线”,从而将形状检测问题转化为参数空间中的峰值检测问题。一、霍夫变换基本思想输入:边缘图像(如经过Canny边缘检测)输出:一组满足几何模型的形状(如直线、圆)关键思想:图像空间中的一个点→参数空间中的一个曲线参数空
- 用OpenCV标定相机内参应用示例(C++和Python)
下面是一个完整的使用OpenCV进行相机内参标定(CameraCalibration)的示例,包括C++和Python两个版本,基于棋盘格图案标定。一、目标:相机标定通过拍摄多张带有棋盘格图案的图像,估计相机的内参:相机矩阵(内参)K畸变系数distCoeffs可选外参(R,T)标定精度指标(如重投影误差)二、棋盘格参数设置(根据自己的棋盘格设置):棋盘格角点数:9x6(内角点,9列×6行);每个
- centos7安装 mysql5.7(安装包)
heiPony
linuxmysqlmariadbcentosmysql
一.卸载centos7自带数据库查看系统自带的Mariadbrpm-qa|grepmariadbmariadb-libs-5.5.44-2.el7.centos.x86_64卸载rpm-e--nodepsmariadb-libs-5.5.44-2.el7.centos.x86_64删除etc目录下的my.cnfrm/etc/my.cnf二.检查mysql是否存在(有就卸载,删除相关文件)rpm-q
- Vue3+Vite+TS+Axios整合详细教程
老马聊技术
VueViteTSvue.js
1.Vite简介Vite是新一代的前端构建工具,在尤雨溪开发Vue3.0的时候诞生。类似于Webpack+Webpack-dev-server。其主要利用浏览器ESM特性导入组织代码,在服务器端按需编译返回,完全跳过了打包这个概念,服务器随起随用。生产中利用Rollup作为打包工具,号称下一代的前端构建工具。vite是一种新型的前端构建工具,能够显著的提升前端开发者的体验。它主要有俩部分组成:一个
- Anaconda 详细下载与安装教程
Anaconda详细下载与安装教程1.简介Anaconda是一个用于科学计算的开源发行版,包含了Python和R的众多常用库。它还包括了conda包管理器,可以方便地安装、更新和管理各种软件包。2.下载Anaconda2.1访问官方网站首先,打开浏览器,访问Anaconda官方网站。2.2选择适合的版本在页面中,你会看到两个主要的下载选项:AnacondaIndividualEdition:适用于
- C++设计模式:简单工厂、工厂方法、抽象工厂
起个别名
C++算法c++
1.工厂模式的特点在我们现实生活中,买馒头和自己蒸馒头、去饭店点一份大盘鸡和自己养鸡,杀鸡,做大盘鸡,这是全然不同的两种体验:自己做麻烦,而且有失败的风险,需要自己承担后果。买现成的,可以忽略制作细节,方便快捷并且无风险,得到的肯定是美味的食物。对于后者,就相当于是一个加工厂,通过这个工厂我们就可以得到想要的东西,在程序设计中,这种模式就叫做工厂模式,工厂生成出的产品就是某个类的实例,也就是对象。
- npm proxy setting
kjndppl
[Node.jsJavaScriptnpmhttpsproxypassword
清理npmconfigdeletehttp-proxynpmconfigdeletehttps-proxy具体设置步骤如下:1.执行npmconfig后,将看到下一行提示信息npmconfigls-ltoshowalldefaults.2.执行npmconfigls-l后,在一大长串的settign中找出userconfig项(大概位于倒数第4项)[b]userconfig[/b]="C:\\Us
- MySQL Explain 详解:从入门到精通,让你的 SQL 飞起来
引言:为什么Explain是SQL优化的“照妖镜”?在Java开发中,我们常常会遇到数据库性能瓶颈的问题。一条看似简单的SQL语句,在数据量增长到一定规模后,可能会从毫秒级响应变成秒级甚至分钟级响应,直接拖慢整个应用的性能。此时,你是否曾困惑于:为什么这条SQL突然变慢了?索引明明建了,为什么没生效?到底是哪里出了问题?答案就藏在MySQL的EXPLAIN命令里。EXPLAIN就像一面“照妖镜”,
- kube-scheduler 抢占机制
分享放大价值
kubernetes源码分析kuberneteskube-scheduler抢占
当pod调度失败后,会在PostFilter扩展点执行抢占流程,下面分析相关的代码实现抢占接口//PodNominatorabstractsoperationstomaintainnominatedPods.typePodNominatorinterface{//将pod加入抢占成功的node中AddNominatedPod(pod*PodInfo,nodeNamestring)//将pod从no
- Shader面试题100道之(81-100)
还是大剑师兰特
#Shader综合教程100+大剑师shader面试题shader教程
Shader面试题(第81-100题)以下是第81到第100道Shader相关的面试题及答案:81.Unity中如何实现屏幕空间的热扭曲效果(HeatDistortion)?热扭曲效果可以通过GrabPass抓取当前屏幕图像,然后在片段着色器中使用噪声或动态UV偏移模拟空气扰动,再结合一个透明通道控制扭曲强度来实现。82.Shader中如何实现物体轮廓高亮(OutlineHighlight)?轮廓
- 本地包解决npm error code E404
雅痞yuppie
npm前端node.js
这个错误提示表明npm找不到名为create-vue-admin-cli的包。这是因为你开发的CLI工具还没有发布到npm官方注册表。要解决这个问题,有两种方法:方法一:使用本地开发模式测试1.确保你的CLI已正确链接到全局在你的vue-admin-cli项目根目录下执行:npmlink这会在全局环境中创建一个符号链接,指向你本地的CLI项目。2.使用本地链接的CLI创建项目直接使用命令:vue-
- python中 @注解 及内置注解 的使用方法总结以及完整示例
慧一居士
Pythonpython
在Python中,装饰器(Decorator)使用@符号实现,是一种修改函数/类行为的语法糖。它本质上是一个高阶函数,接受目标函数作为参数并返回包装后的函数。Python也提供了多个内置装饰器,如@property、@staticmethod、@classmethod等。一、核心概念装饰器本质:@decorator等价于func=decorator(func)执行时机:在函数/类定义时立即执行装饰
- Java特性之设计模式【责任链模式】
Naijia_OvO
Java特性java设计模式责任链模式
一、责任链模式概述顾名思义,责任链模式(ChainofResponsibilityPattern)为请求创建了一个接收者对象的链。这种模式给予请求的类型,对请求的发送者和接收者进行解耦。这种类型的设计模式属于行为型模式在这种模式中,通常每个接收者都包含对另一个接收者的引用。如果一个对象不能处理该请求,那么它会把相同的请求传给下一个接收者,依此类推主要解决:职责链上的处理者负责处理请求,客户只需要将
- windows安装pnpm后报错:pnpm : 无法将“pnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。
Ithao2
Vuenpm前端node.js
使用npm方式安装pnpm,命令如下:npminstall-gpnpm安装完以后,执行pnpm-v查看版本号:pnpm-v执行完发现报错:pnpm:无法将“pnpm”项识别为cmdlet、函数、脚本文件或可运行程序的名称。尝试配置环境变量,重启后均不生效。解决方案:使用PowerShell进行安装1.以管理员用户打开PowerShell,执行如下命令:iwrhttps://get.pnpm.io/
- Python中的静态方法和类方法详解
在Python中,`@staticmethod`和`@classmethod`是两种装饰器,它们用于定义类中的方法,但是它们的行为和用途有所不同。###@staticmethod`@staticmethod`装饰器用于定义一个静态方法。静态方法不接收类或实例的引用作为第一个参数,因此它不能访问类的状态或实例的状态。静态方法可以看作是与类关联的普通函数,但它们可以通过类名直接调用。classMath
- 前端 NPM 包的依赖可视化分析工具推荐
前端视界
前端艺匠馆前端npmarcgisai
前端NPM包的依赖可视化分析工具推荐关键词:NPM、依赖管理、可视化分析、前端工程、包管理、依赖冲突、性能优化摘要:本文将深入探讨前端开发中NPM包依赖可视化分析的重要性,介绍5款主流工具的使用方法和特点,并通过实际案例展示如何利用这些工具优化项目依赖结构、解决版本冲突问题以及提升构建性能。文章将帮助开发者更好地理解和掌控项目依赖关系,提高开发效率和项目可维护性。背景介绍目的和范围本文旨在为前端开
- Linux操作系统磁盘管理
CZZDg
linux运维服务器
目录一.硬盘介绍1.硬盘的物理结构2.CHS编号3.磁盘存储划分4.开机流程5.要点6.磁盘存储数据的形式二.Linux文件系统1.根文件系统2.虚拟文件系统3.真文件系统4.伪文件系统三.磁盘分区与挂载1.磁盘分区方式2.分区命令3.查看与识别命令4.格式化命令5.挂载命令四.LVM逻辑卷1.概述2.管理命令五.磁盘配额1.概述usrquota:支持对用户的磁盘配额grpquota:支持对组的磁
- 计算机网络技术
CZZDg
计算机网络
目录一.网络概述1.网络的概念2.网络发展是3.网络的四要素4.网络功能5.网络类型6.网络协议与标准7.网络中常见的概念8.网络拓补结构二.网络模型1.分层思想2.OSI七层模型3.TCP/IP五层模型4.数据的封装与解封装过程三.IP地址1.进制转换2.IP地址定义3.IP地址组成成分4.IP地址分类5.地址划分6、相关概念一.网络概述1.网络的概念两个主机通过传输介质和通信协议实现通信和资源
- cesium添加原生MVT矢量瓦片方案
zhu_zhu_xia
cesiumvuearcgiscesiumwebgljavascript
项目中需要基于cesium接入mvt格式的服务并支持属性拾取查询,通过一系列预研测试,最后选择cesium-mvt-imagery-provider开源插件完成,关键源码信息如下:npmicesiumcesium-mvt-imagery-provider//安装依赖包//加载图层importCesiumMVTImageryProviderfrom"cesium-mvt-imagery-provid
- npm 切换 node 版本 和npm的源
爱敲代码的小冰
npm前端node.js
在开发过程中,不同项目可能需要不同版本的Node.js,同时于由XX原因,我们需要切换npm的源。这时如果需要切换node版本或者npm的源,我们可以使用以下方法。使用nvm切换Node版本1、安装npminstallnvm-g2、使用#列出所有可用版本nvmlist-remote#安装指定版本nvminstall16.15.1#使用指定版本nvmuse16.15.1#查看当前使用的版本nvmcu
- Python中类静态方法:@classmethod/@staticmethod详解和实战示例
在Python中,类方法(@classmethod)和静态方法(@staticmethod)是类作用域下的两种特殊方法。它们使用装饰器定义,并且与实例方法(deffunc(self))的行为有所不同。1.三种方法的对比概览方法类型是否访问实例(self)是否访问类(cls)典型用途实例方法✅是❌否访问对象属性类方法@classmethod❌否✅是创建类的替代构造器,访问类变量等静态方法@stati
- 日历插件-FullCalendar的详细使用
老马聊技术
JavaScript前端javascript
一、介绍FullCalendar是一个功能强大、高度可定制的JavaScript日历组件,用于在网页中显示和管理日历事件。它支持多种视图(月、周、日等),可以轻松集成各种框架,并提供丰富的事件处理功能。二、实操案例具体代码如下:FullCalendar日期选择body{font-family:Arial,sans-serif;margin:20px;}#calendar{max-width:900
- EasyCwmp源码分析与接口实现详解:深入理解源码架构,掌握核心接口
EasyCwmp源码分析与接口实现详解:深入理解源码架构,掌握核心接口去发现同类优质开源项目:https://gitcode.com/在开源项目中,寻找一款能够提升开发效率、简化流程的工具是每个开发者的追求。今天,我们要介绍的这款开源项目EasyCwmp,正是为了帮助开发者深入了解源码架构,掌握核心接口实现,从而加速项目开发进程。以下是关于EasyCwmp源码分析与接口实现详解的项目推荐文章。项目
- Python多版本管理与pip升级全攻略:解决冲突与高效实践
码界奇点
Pythonpythonpip开发语言python3.11源代码管理虚拟现实依赖倒置原则
引言Python作为最流行的编程语言之一,其版本迭代速度与生态碎片化给开发者带来了巨大挑战。据统计,超过60%的Python开发者需要同时维护基于Python3.6+和Python2.7的项目。本文将系统解决以下核心痛点:如何安全地在同一台机器上管理多个Python版本pip依赖冲突的根治方案符合PEP标准的生产环境最佳实践第一部分:Python多版本管理核心方案1.1系统级多版本共存方案Wind
- ThinkSound V2版 - 一键给无声视频配音,为AI视频生成匹配音效 支持50系显卡 一键整合包下载
昨日之日2006
ai语音音视频人工智能
ThinkSound是阿里通义实验室开源的首个音频生成模型,它能够让AI像专业“音效师”一样,根据视频内容生成高度逼真、与视觉内容完美契合的音频。ThinkSound可直接应用于影视后期制作,为AI生成的视频自动匹配精准的环境噪音与爆炸声效;服务于游戏开发领域,实时生成雨势变化等动态场景的自适应音效;同时可以无障碍视频生产,为视障用户同步生成画面描述与环境音效。今天分享的ThinkSoundV2版
- Java常用排序算法/程序员必须掌握的8大排序算法
cugfy
java
分类:
1)插入排序(直接插入排序、希尔排序)
2)交换排序(冒泡排序、快速排序)
3)选择排序(直接选择排序、堆排序)
4)归并排序
5)分配排序(基数排序)
所需辅助空间最多:归并排序
所需辅助空间最少:堆排序
平均速度最快:快速排序
不稳定:快速排序,希尔排序,堆排序。
先来看看8种排序之间的关系:
1.直接插入排序
(1
- 【Spark102】Spark存储模块BlockManager剖析
bit1129
manager
Spark围绕着BlockManager构建了存储模块,包括RDD,Shuffle,Broadcast的存储都使用了BlockManager。而BlockManager在实现上是一个针对每个应用的Master/Executor结构,即Driver上BlockManager充当了Master角色,而各个Slave上(具体到应用范围,就是Executor)的BlockManager充当了Slave角色
- linux 查看端口被占用情况详解
daizj
linux端口占用netstatlsof
经常在启动一个程序会碰到端口被占用,这里讲一下怎么查看端口是否被占用,及哪个程序占用,怎么Kill掉已占用端口的程序
1、lsof -i:port
port为端口号
[root@slave /data/spark-1.4.0-bin-cdh4]# lsof -i:8080
COMMAND PID USER FD TY
- Hosts文件使用
周凡杨
hostslocahost
一切都要从localhost说起,经常在tomcat容器起动后,访问页面时输入http://localhost:8088/index.jsp,大家都知道localhost代表本机地址,如果本机IP是10.10.134.21,那就相当于http://10.10.134.21:8088/index.jsp,有时候也会看到http: 127.0.0.1:
- java excel工具
g21121
Java excel
直接上代码,一看就懂,利用的是jxl:
import java.io.File;
import java.io.IOException;
import jxl.Cell;
import jxl.Sheet;
import jxl.Workbook;
import jxl.read.biff.BiffException;
import jxl.write.Label;
import
- web报表工具finereport常用函数的用法总结(数组函数)
老A不折腾
finereportweb报表函数总结
ADD2ARRAY
ADDARRAY(array,insertArray, start):在数组第start个位置插入insertArray中的所有元素,再返回该数组。
示例:
ADDARRAY([3,4, 1, 5, 7], [23, 43, 22], 3)返回[3, 4, 23, 43, 22, 1, 5, 7].
ADDARRAY([3,4, 1, 5, 7], "测试&q
- 游戏服务器网络带宽负载计算
墙头上一根草
服务器
家庭所安装的4M,8M宽带。其中M是指,Mbits/S
其中要提前说明的是:
8bits = 1Byte
即8位等于1字节。我们硬盘大小50G。意思是50*1024M字节,约为 50000多字节。但是网宽是以“位”为单位的,所以,8Mbits就是1M字节。是容积体积的单位。
8Mbits/s后面的S是秒。8Mbits/s意思是 每秒8M位,即每秒1M字节。
我是在计算我们网络流量时想到的
- 我的spring学习笔记2-IoC(反向控制 依赖注入)
aijuans
Spring 3 系列
IoC(反向控制 依赖注入)这是Spring提出来了,这也是Spring一大特色。这里我不用多说,我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC,下面我将介绍不用Spring的IoC。
IoC不是框架,她是java的技术,如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明:
如:程序中有 Mysql.calss 、Oracle.class 、SqlSe
- 高性能mysql 之 选择存储引擎(一)
annan211
mysqlInnoDBMySQL引擎存储引擎
1 没有特殊情况,应尽可能使用InnoDB存储引擎。 原因:InnoDB 和 MYIsAM 是mysql 最常用、使用最普遍的存储引擎。其中InnoDB是最重要、最广泛的存储引擎。她 被设计用来处理大量的短期事务。短期事务大部分情况下是正常提交的,很少有回滚的情况。InnoDB的性能和自动崩溃 恢复特性使得她在非事务型存储的需求中也非常流行,除非有非常
- UDP网络编程
百合不是茶
UDP编程局域网组播
UDP是基于无连接的,不可靠的传输 与TCP/IP相反
UDP实现私聊,发送方式客户端,接受方式服务器
package netUDP_sc;
import java.net.DatagramPacket;
import java.net.DatagramSocket;
import java.net.Ine
- JQuery对象的val()方法执行结果分析
bijian1013
JavaScriptjsjquery
JavaScript中,如果id对应的标签不存在(同理JAVA中,如果对象不存在),则调用它的方法会报错或抛异常。在实际开发中,发现JQuery在id对应的标签不存在时,调其val()方法不会报错,结果是undefined。
- http请求测试实例(采用json-lib解析)
bijian1013
jsonhttp
由于fastjson只支持JDK1.5版本,因些对于JDK1.4的项目,可以采用json-lib来解析JSON数据。如下是http请求的另外一种写法,仅供参考。
package com;
import java.util.HashMap;
import java.util.Map;
import
- 【RPC框架Hessian四】Hessian与Spring集成
bit1129
hessian
在【RPC框架Hessian二】Hessian 对象序列化和反序列化一文中介绍了基于Hessian的RPC服务的实现步骤,在那里使用Hessian提供的API完成基于Hessian的RPC服务开发和客户端调用,本文使用Spring对Hessian的集成来实现Hessian的RPC调用。
定义模型、接口和服务器端代码
|---Model
&nb
- 【Mahout三】基于Mahout CBayes算法的20newsgroup流程分析
bit1129
Mahout
1.Mahout环境搭建
1.下载Mahout
http://mirror.bit.edu.cn/apache/mahout/0.10.0/mahout-distribution-0.10.0.tar.gz
2.解压Mahout
3. 配置环境变量
vim /etc/profile
export HADOOP_HOME=/home
- nginx负载tomcat遇非80时的转发问题
ronin47
nginx负载后端容器是tomcat(其它容器如WAS,JBOSS暂没发现这个问题)非80端口,遇到跳转异常问题。解决的思路是:$host:port
详细如下:
该问题是最先发现的,由于之前对nginx不是特别的熟悉所以该问题是个入门级别的:
? 1 2 3 4 5
- java-17-在一个字符串中找到第一个只出现一次的字符
bylijinnan
java
public class FirstShowOnlyOnceElement {
/**Q17.在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b
* 1.int[] count:count[i]表示i对应字符出现的次数
* 2.将26个英文字母映射:a-z <--> 0-25
* 3.假设全部字母都是小写
*/
pu
- mongoDB 复制集
开窍的石头
mongodb
mongo的复制集就像mysql的主从数据库,当你往其中的主复制集(primary)写数据的时候,副复制集(secondary)会自动同步主复制集(Primary)的数据,当主复制集挂掉以后其中的一个副复制集会自动成为主复制集。提供服务器的可用性。和防止当机问题
mo
- [宇宙与天文]宇宙时代的经济学
comsci
经济
宇宙尺度的交通工具一般都体型巨大,造价高昂。。。。。
在宇宙中进行航行,近程采用反作用力类型的发动机,需要消耗少量矿石燃料,中远程航行要采用量子或者聚变反应堆发动机,进行超空间跳跃,要消耗大量高纯度水晶体能源
以目前地球上国家的经济发展水平来讲,
- Git忽略文件
Cwind
git
有很多文件不必使用git管理。例如Eclipse或其他IDE生成的项目文件,编译生成的各种目标或临时文件等。使用git status时,会在Untracked files里面看到这些文件列表,在一次需要添加的文件比较多时(使用git add . / git add -u),会把这些所有的未跟踪文件添加进索引。
==== ==== ==== 一些牢骚
- MySQL连接数据库的必须配置
dashuaifu
mysql连接数据库配置
MySQL连接数据库的必须配置
1.driverClass:com.mysql.jdbc.Driver
2.jdbcUrl:jdbc:mysql://localhost:3306/dbname
3.user:username
4.password:password
其中1是驱动名;2是url,这里的‘dbna
- 一生要养成的60个习惯
dcj3sjt126com
习惯
一生要养成的60个习惯
第1篇 让你更受大家欢迎的习惯
1 守时,不准时赴约,让别人等,会失去很多机会。
如何做到:
①该起床时就起床,
②养成任何事情都提前15分钟的习惯。
③带本可以随时阅读的书,如果早了就拿出来读读。
④有条理,生活没条理最容易耽误时间。
⑤提前计划:将重要和不重要的事情岔开。
⑥今天就准备好明天要穿的衣服。
⑦按时睡觉,这会让按时起床更容易。
2 注重
- [介绍]Yii 是什么
dcj3sjt126com
PHPyii2
Yii 是一个高性能,基于组件的 PHP 框架,用于快速开发现代 Web 应用程序。名字 Yii (读作 易)在中文里有“极致简单与不断演变”两重含义,也可看作 Yes It Is! 的缩写。
Yii 最适合做什么?
Yii 是一个通用的 Web 编程框架,即可以用于开发各种用 PHP 构建的 Web 应用。因为基于组件的框架结构和设计精巧的缓存支持,它特别适合开发大型应
- Linux SSH常用总结
eksliang
linux sshSSHD
转载请出自出处:http://eksliang.iteye.com/blog/2186931 一、连接到远程主机
格式:
ssh name@remoteserver
例如:
ssh
[email protected]
二、连接到远程主机指定的端口
格式:
ssh name@remoteserver -p 22
例如:
ssh i
- 快速上传头像到服务端工具类FaceUtil
gundumw100
android
快速迭代用
import java.io.DataOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOExceptio
- jQuery入门之怎么使用
ini
JavaScripthtmljqueryWebcss
jQuery的强大我何问起(个人主页:hovertree.com)就不用多说了,那么怎么使用jQuery呢?
首先,下载jquery。下载地址:http://hovertree.com/hvtart/bjae/b8627323101a4994.htm,一个是压缩版本,一个是未压缩版本,如果在开发测试阶段,可以使用未压缩版本,实际应用一般使用压缩版本(min)。然后就在页面上引用。
- 带filter的hbase查询优化
kane_xie
查询优化hbaseRandomRowFilter
问题描述
hbase scan数据缓慢,server端出现LeaseException。hbase写入缓慢。
问题原因
直接原因是: hbase client端每次和regionserver交互的时候,都会在服务器端生成一个Lease,Lease的有效期由参数hbase.regionserver.lease.period确定。如果hbase scan需
- java设计模式-单例模式
men4661273
java单例枚举反射IOC
单例模式1,饿汉模式
//饿汉式单例类.在类初始化时,已经自行实例化
public class Singleton1 {
//私有的默认构造函数
private Singleton1() {}
//已经自行实例化
private static final Singleton1 singl
- mongodb 查询某一天所有信息的3种方法,根据日期查询
qiaolevip
每天进步一点点学习永无止境mongodb纵观千象
// mongodb的查询真让人难以琢磨,就查询单天信息,都需要花费一番功夫才行。
// 第一种方式:
coll.aggregate([
{$project:{sendDate: {$substr: ['$sendTime', 0, 10]}, sendTime: 1, content:1}},
{$match:{sendDate: '2015-
- 二维数组转换成JSON
tangqi609567707
java二维数组json
原文出处:http://blog.csdn.net/springsen/article/details/7833596
public class Demo {
public static void main(String[] args) { String[][] blogL
- erlang supervisor
wudixiaotie
erlang
定义supervisor时,如果是监控celuesimple_one_for_one则删除children的时候就用supervisor:terminate_child (SupModuleName, ChildPid),如果shutdown策略选择的是brutal_kill,那么supervisor会调用exit(ChildPid, kill),这样的话如果Child的behavior是gen_
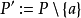 可以被k个不相交的链
可以被k个不相交的链
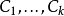 覆盖,且最少存在一个大小为k的反链
覆盖,且最少存在一个大小为k的反链
 。显然,
。显然,
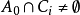 ,
,
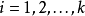 。令
。令
 为
为
 的极大值,
的极大值,
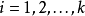 ,
,
 为
为
 中大小为k的反链,令
中大小为k的反链,令
 ,
,
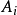 为包含
为包含
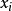 的大小为k的反链。确定任意不等的索引
的大小为k的反链。确定任意不等的索引
 ,那么
,那么
 。令
。令
 ,根据
,根据
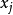 的定义,
的定义,
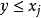 。因此,由
。因此,由
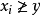 推断出
推断出
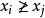 。通过交换
。通过交换
 ,可以得到
,可以得到
 。由此得证,A为反链。
。由此得证,A为反链。
 ,
,
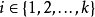 。令K为链
。令K为链
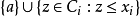 。那么,通过选择
。那么,通过选择
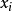 ,使得
,使得
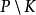 不包含大小为k的反链。由于
不包含大小为k的反链。由于
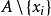 是
是
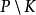 中大小为k-1的反链,归纳推出
中大小为k-1的反链,归纳推出
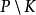 可以被k-1个不相交的链覆盖。因此,正如所需要证明的,P可以被k个不相交的链覆盖。其次,如果
可以被k-1个不相交的链覆盖。因此,正如所需要证明的,P可以被k个不相交的链覆盖。其次,如果
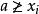 ,
,
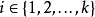 ,那么由于a是P的极大值,
,那么由于a是P的极大值,
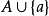 为P中大小为k+1的反链。现在,P可以被k+1个链
为P中大小为k+1的反链。现在,P可以被k+1个链
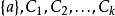 覆盖。到此,定理全部证明结束。
覆盖。到此,定理全部证明结束。