数据分析师
数据分析师
第二章-描述性统计分析
数据的计量尺度和具体的统计方法息息相关,大致分为3类,分别是名义测量、次序测量和连续变量测量这三类测量分别对应三种变量类型,即分类变量,顺序变量和数值变量。连续变量测量可以进一步细分为间距测量和比例测量。间距测量和比率测量这两种测量,统计软件通常不做区分,大部分的模型都适用。
名义测量( nominal measurement)是最低的一种测量等级,也称定名测度。其数值仅代表某些分类或属性。比如用来表示性别(1或2)和民族(1、2、3...)等。这类变量一般不做高低、大小区分。名义测量没有大小等级,只是数字符号
次序测量( ordinal measurement)的量化水平高于名义测量,用于测量的数值代表了一些有序分类。比如,用来表示受教育程度高低的数字(1、2、3..)具有一定的顺序性。次序测量是有等级和顺序的
间距测量( interval measurement)的量化程度更高一些,它的取值不再是类的编码,而是采用一定单位的实际测量值。可以进行加减运算,但不能进行乘除运算,因为测量等级变量所取的“O”值,不是物理上的绝对“”。比如,考试成绩的零分,不能说这个学生一点英语能力也没有。间距测量具有实际意义,可以进行加减乘除
比率测量( ratio measurement)是最高级的测量等级,它除了具有间距测度等级的所有性质外,其0值具有物理上的绝对意义,而且可以进行加减乘除运算。例如增长率、收入等。
数据描述
分类变量
对于分类变量,通常可以检查变量的众数、分类取值的百分比间的差别大小,有无太小的比例(异常值),主要的统计量如下:
●频次频数:每个水平出现的次数;
●百分比:每个水平出现的频数除以总数;
●累积频次与累积百分比:仅对于次序型变量有意义,分别计算累积频次和百分比。
顺序变量
对于顺序变量,通常检测数据的众数、频次、百分比、累积频次与累积百分比,四分位差等
连续变量(重点)
对于连续变量,通常检查中心水平、离散程度、偏度和峰度4个方面
值得注意的是分类变量、顺序变量、连续变量的量化水平是由低到高的,低水平变量的统计量可以用于高水平,但高水平变量的统计量不一定能用于低水平。例如分类变量的统计量可以用于连续变量,但反之则不一定成立。
连续变量中心水平
能代表“中心”概念的可选统计量有均值、中位数和众数。
众数:出现次数最多的变量值,一组数据可能没有众数或有几个众数。例如:数据23,4,4,5,5,7,8,23,78,其中4和5出现了两次,则4和5都是众数。
中位数:排序后处于中间位置上的值,这里需要注意的是,一定要先排序。
// M=\begin{cases} x_{(\frac{n+1}{2})}, & \text { $n$ 为奇数} \\ \frac{1}{2}[x_{\frac{n}{2}}+x_{(\frac{n}{2}+1)}], & \text{ $n$为偶数} \end{cases} //
这里的n表示数据数量
例如,数据1,2,6,5,4,3排序后为12,3,4,5,6,这里n=6,是偶数,所以该数据的中位数为(3+4)/2=2.5
连续变量中心水平
四分位数:是另外一套表达变量位置信息的手段,其定义方式类似于中位数。中位数本身就是变量从大到小排序后,50%对应的变量取值。如图:
这里的Q1称为下四分位数,Q3称为上四份位数,Q2就是中位数。
连续变量---中心水平(算数平均数)
样本平均数
// \overline{x}=\frac{x_1+x_2+...+x_n}{n}=\frac{\sum^n_{i=1}x_i}{n} //
总体平均数
// \mu=\frac{x_1+x_2+...+x_{N}}{N}=\frac{\sum^N_{i=1}x_i}{N} //
这里的n是样本数据量,N是总体数据量,样本是用来估计总体的。一般样本用英文字母,而总体用希腊字母
连续变量---中心水平(加权平均数)
样本加权平均
// \overline{x}=\frac{x_1f_1+x_2f+2+...+x_kf_k}{f_1+f_2+...+f_k}=\frac{\sum^k_{i=1}x_if_i}{n} //
总体加权平均
// \mu=\frac{x_1f_1+x_2f_2+...+x_kf_k}{f_1+f_2+...+f_k}=\frac{\sum^k_{i=1}x_if_i}{N} //
这里的
// x_1,x_2,...x_k //
表示各组数据的组中值或数据本身,
// f_1,f_2,...f_k //
表示各组频数或数据的权重
连续变量---中心水平(几何平均数)
适用于计算比率数据的平均,主要用于计算平均增长率。
// G = \sqrt[n]{x_1*x_2*...*x_n}=\sqrt[n]{\prod^n_{i=1}x_i} //
各个中心水平度量的比较:
众数和中位数不易受到极端值的影响,平均数容易受到极端值得影响。众数和中位数适合在非对称情况下使用,众数不是唯一的。
连续变量离散程度
知道一个变量的“中心”水平统计量之后,还想知道这个指标到底有多大的代表性。如果这个变量的变化范围非常小,甚至是常数,那么这个水平变量就非常有代表意义;如果这个变量的变化范围非常大,么水平指标的代表性就相对下降。如下表所示,列出了5个常用的离散程度度量指标。
| 离散程度度量指标 | 定义 |
|---|---|
| 异众比率 | 非众数组的频数占总频数的比例 |
| 极差 | 最大值-最小值 |
| 四分位差 | 上分位数-下分位数 |
| 方差 | 测量变量取之偏离自身均值的程度 |
| 标准差 | 方差开根号(和变量原有取值具有同样的量纲) |
* 异众比率公式:
// r=\frac{\sum f_i-f_m}{\sum f_i}=1-\frac{fm}{\sum f_i} //
这里的
// f_m //
表示众数的频率
* 方差公式:
* 总体方差 :
// \sigma^2=\frac{\sum^N_{i=1}(x_i-\mu)^2}{N} //
* 样本方差 :
// S^2=\frac{\sum^n_{i=1}(x_i-\mu)^2}{n-1} //
* 标准差公式:
* 总体标准差 :
// \sigma = \sqrt{\frac{\sum^N_{i=1}(x_i-\mu)^2}{N}} //
* 样本标准差 :
// S=\sqrt{\frac{\sum^n_{i=1}(x_i-\overline{x})^2}{n-1}} //
方差在统计学中也称为二阶中心距,实际是该变量每个取值到均值之间的距离均值。方差在很多参数统计的推导公式中出现,但是实际描述性统计中使用的不多。主要是方差的单位比较特殊,不容易理解。标准差是描述分析中使用最多的,因为标准差的单位和原始变量相同。
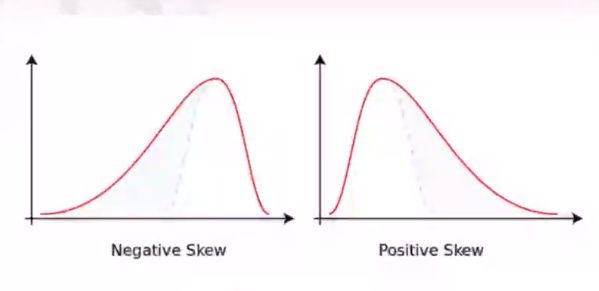
连续变量——偏度
偏度用来刻画偏态的程度。偏态有两种情况:一种是如下图所示(左边)的左偏,该变量在负的方向部分严重拖尾;另一种是如下图所示(右边)的右偏,在正的方向部分严重拖尾。在实际经济和商业数据分析中,右偏是比较普遍的状态。比如,地区的居民收入、客户购买产品的数量、金额和保险理赔额。
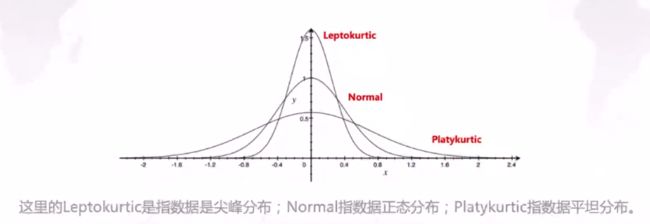
连续变量——峰度
峰度反应的是变量向两边拖尾的情况。相比正态分布而言,如果一个变量是尖峰的,则必然会导致两边拖尾情况更严重,反映到统计学中就会出现超过2倍标准差数值的概率会大于5%,超过3倍标准差数值的概率会大于1%。这表明出现较大偏离值的可能性提高了。资产收益率的峰度在金融研究中是比较受关注的,这表明了该资产的风险分布情况,尾越厚,风险越大。
图形描述
条形图
条形图是一个很好展现变量分布情况的方式,但是连续变量不可能做出条形图因为连续变量如果精度足够大的话,每个取值出现的频数应该只有一次。但是可以采用将连续变量分箱的方法做直方图这样,每个柱代表一个分箱,柱高为在这个分箱中的取值出现的次数或百分比,分箱的数量和间隔可以自定义,如下图所示:
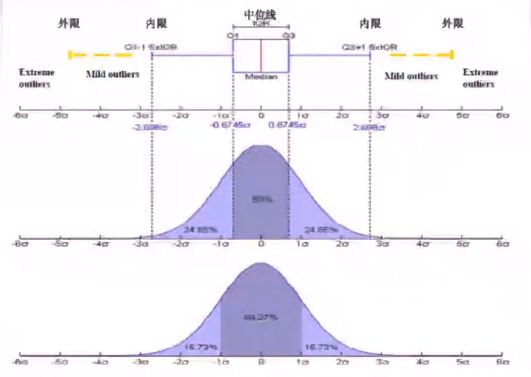
盒须图
盒须图(又称箱线图)相对于直方图而言,提供的信息更精炼。它提供了中位数、均值、上下分位点的信息,这不但可以了解变量的中心水平,还可以了解变量的变化范围。其中需要说明的是最大值和最小值,它们不是变量的最大值和最小值。如图1-9所示,以盒须图中的最小值为例,从上分位点加上1.5倍的内分位距(IQR),该变量在这个范围内的最大取值被称为最大值,超过1.5倍的内分位距的取值被称为离群值(异常值)。
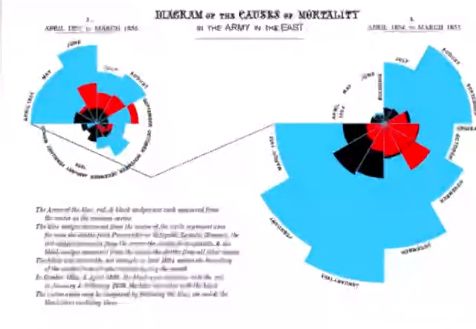
玫瑰图
玫瑰图又称为南丁格尔玫瑰图。南丁格尔( Floarence Nightinggale),英国护士和统计学家。1883年,南丁格尔撰写影响英国军队健康,效率和医院管理的资料中,她创造了一个非凡的原创图形展示方式(如下图所示),这张图显示了人们在1854年7月至次年年底期间死亡的情况。
南丁格尔玫瑰图类似于饼图的变形,它可以用转角、扇形面积、以及颜色展现数据的不同维度。