LeetCode #279 Perfect Squares

Question

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

Example 1:

Input: n = 12
Output: 3 
Explanation: 12 = 4 + 4 + 4.

Example 2:

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

方法一：动态规划

time complexity：O(n^2)

很容易想到动态规划的方法，先求出1, 2, 3, ..., n-1的最小平方数个数值，再求出n的最小平方数个数值。动态转移方程为：

f(i) = min([ f[k]+f[i-k] for k in range(1, i)] )

class Solution:
    def numSquares(self, n: int) -> int:
        import math
        f = [0]
        f.append(1)
        for i in range(2, n+1):
            if i == int((math.sqrt(i))) ** 2:
                f.append(1)
            else:
                f.append(min([f[k]+f[i-k] for k in range(1, i)]))
        return f[n]

TLE，时间复杂度太高，502 / 588 test cases passed.

方法二：动态规划，开方剪枝

time complexity：O(n*sqrt(n))

方法一的大体思路不错，但由于枚举了1, 2, 3, ..., i-1所有的值，导致此步用了O(n)，但其实没必要枚举1, 2, 3, ..., i-1之间配对的值，只需要枚举完全平方数就行了，所以可以改进为只对完全平方数进行枚举。

class Solution:
    def numSquares(self, n: int) -> int:
        f = [n] * (n+1)
        f[0] = 0
        f[1] = 1
        for i in range(2, n+1):
            j = 1
            while j*j <= i:
                f[i] = min(f[i], f[i-j*j]+1)
                j+=1
        return f[-1]

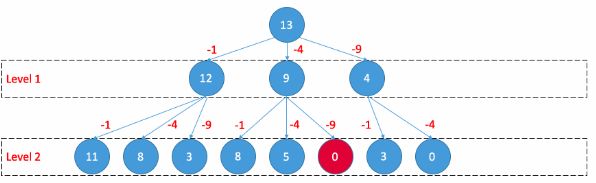
方法三：BFS

time complexity：O(sqrt(n) ^ k) （k平均情况不确定，由方法四可知，最坏情况是4）

以13为例：

 

方法四：四平方和定理

time complexity：

 

 

 

参考：

https://blog.csdn.net/qq_39445165/article/details/89479142

https://blog.csdn.net/qq_17550379/article/details/80875782