干货 | Branch and Price算法求解VRPTW问题（附JAVA代码分享）

前言

前两天小编刚忙完手头上的事情，闲了下来，然后顺便研究了一下Branch and Price的算法。刚好，国内目前缺少这种类型算法的介绍和代码实现，今天就给大家分享一下咯。

代码出自国外一个大神@author mschyns之手。代码没有写调用模块，这一部分是小编后续补上去的，以便大家能运行（真是太贴心啦呜呜呜~还不赶紧转发点赞！）。然后检查了代码，修正了一些bug。

代码获取方式：关注公众号！

在公众号后台回复【BPVRPTW】不包括【】即可。

算法介绍

该Branch and Price算法由以下几部分组成：

1. Branch and Bound：分支定界，下界使用Column Generation求解。

2. Column Generation：列生成算法，求解VRPWTW松弛模型的最优解。

3. ESPPRC-Label Setting：求解VRPTW的子问题(pricing problem)，标号法求解。

算法的运行效果如下：

算例用的是标准Solomon25。大部分，一轮Column Generation就能直接得到整数解，可能是巧合。也有部分算例需要branch。

更改输入算例在Main.java:

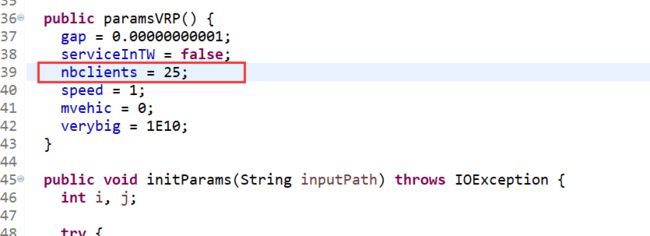
更改算例后同时也要更改客户数，在paramsVRP.java:

可参考的推文如下

CPLEX：

1. 干货 | cplex介绍、下载和安装以及java环境配置和API简单说明

2. 干货 | JAVA调用cplex求解一个TSP模型详解

3. 干货|十分钟快速掌握CPLEX求解VRPTW数学模型（附JAVA代码及CPLEX安装流程）

Branch and Bound

1. 干货 | 10分钟带你全面掌握branch and bound（分支定界）算法-概念篇

2. 干货 | 10分钟搞懂branch and bound算法的代码实现附带java代码

3. 干货 | 10分钟教你用branch and bound（分支定界）算法求解TSP旅行商问题

4. cplex教学 | 分支定界法(branch and bound)解带时间窗的车辆路径规划问题（附代码及详细注释）

Column Generation

1. 干货 | 10分钟带你彻底了解Column Generation（列生成）算法的原理附java代码

2. 运筹学教学|列生成（Column Generation）算法（附代码及详细注释）

3. 干货 | 10分钟教你使用Column Generation求解VRPTW的线性松弛模型

4. 干货 | 求解VRPTW松弛模型的Column Generation算法的JAVA代码分享

ESPPRC

1. 干货 | VRPTW子问题ESPPRC的介绍及其求解算法的C++代码
2. 标号法(label-setting algorithm)求解带时间窗的最短路问题

可参考的文献如下

BOOK: Desrosiers, Desaulniers, Solomon, "Column Generation", Springer, 2005 (GERAD, 25th anniversary)

Column generation : chapter 3, Vehicle Routing Problem with Time Windows Brian Kallehauge, Jesper Larsen, Oli B. G, Madsen, and Marius M. Solomon

Pricing SPPRC : chapter 2, Shortest Path Problems with Resource Constraints 33 Stefan Irnich and Guy Desaulniers

文献下载请关注公众号！

在后台回复【BPREF】不包括【】即可下载。

代码解析如下

Branch and Bound的过程如下（具体参考此前讲过的算法原理）：

  public boolean BBnode(paramsVRP userParam, ArrayList routes,
      treeBB branching, ArrayList bestRoutes, int depth)
      throws IOException {
    // userParam (input) : all the parameters provided by the users (cities,
    // roads...)
    // routes (input) : all (but we could decide to keep only a subset) the
    // routes considered up to now (to initialize the Column generation process)
    // branching (input): BB branching context information for the current node
    // to process (branching edge var, branching value, branching from...)
    // bestRoutes (output): best solution encountered
    int i, j, bestEdge1, bestEdge2, prevcity, city, bestVal;
    double coef, bestObj, change, CGobj;
    boolean feasible;

    try {

      // check first that we need to solve this node. Not the case if we have
      // already found a solution within the gap precision
      if ((upperbound - lowerbound) / upperbound < userParam.gap)
        return true;

      // init
      if (branching == null) { // root node - first call
        // first call - root node
        treeBB newnode = new treeBB();
        newnode.father = null;
        newnode.toplevel = true;
        newnode.branchFrom = -1;
        newnode.branchTo = -1;
        newnode.branchValue = -1;
        newnode.son0 = null;
        branching = newnode;
      }

      // display some local info
      if (branching.branchValue < 1)
        System.out.println("\nEdge from " + branching.branchFrom + " to "
            + branching.branchTo + ": forbid");
      else
        System.out.println("\nEdge from " + branching.branchFrom + " to "
            + branching.branchTo + ": set");
      int mb = 1024 * 1024;
      Runtime runtime = Runtime.getRuntime();
      System.out.print("Java Memory=> Total:" + (runtime.totalMemory() / mb)
          + " Max:" + (runtime.maxMemory() / mb) + " Used:"
          + ((runtime.totalMemory() - runtime.freeMemory()) / mb) + " Free: "
          + runtime.freeMemory() / mb);

      // Compute a solution for this node using Column generation
      columngen CG = new columngen();

      CGobj = CG.computeColGen(userParam, routes);
      // feasible ? Does a solution exist?
      if ((CGobj > 2 * userParam.maxlength) || (CGobj < -1e-6)) { 
        // can only be true when the routes in the solution include forbidden edges (can happen when the BB set branching values)
        System.out.println("RELAX INFEASIBLE | Lower bound: " + lowerbound
            + " | Upper bound: " + upperbound + " | Gap: "
            + ((upperbound - lowerbound) / upperbound) + " | BB Depth: "
            + depth + " | " + routes.size() + " routes");
        return true; // stop this branch
      }
      branching.lowestValue = CGobj;

      // update the global lowerbound when required
      if ((branching.father != null) && (branching.father.son0 != null)
          && branching.father.toplevel) {
        // all nodes above and on the left have been processed=> we can compute
        // a new lowerbound
        lowerbound = (branching.lowestValue > branching.father.son0.lowestValue) ? branching.father.son0.lowestValue
            : branching.lowestValue;
        branching.toplevel = true;
      } else if (branching.father == null) // root node
        lowerbound = CGobj;

      if (branching.lowestValue > upperbound) {
        CG = null;
        System.out.println("CUT | Lower bound: " + lowerbound
            + " | Upper bound: " + upperbound + " | Gap: "
            + ((upperbound - lowerbound) / upperbound) + " | BB Depth: "
            + depth + " | Local CG cost: " + CGobj + " | " + routes.size()
            + " routes");
        return true; // cut this useless branch
      } else {
        // ///////////////////////////////////////////////////////////////////////////
        // check the (integer) feasibility. Otherwise search for a branching
        // variable
        feasible = true;
        bestEdge1 = -1;
        bestEdge2 = -1;
        bestObj = -1.0;
        bestVal = 0;

        // transform the path variable (of the CG model) into edges variables
        for (i = 0; i < userParam.nbclients + 2; i++)
          java.util.Arrays.fill(userParam.edges[i], 0.0);
        for (route r : routes) {
          if (r.getQ() > 1e-6) { // we consider only the routes in the current
                                 // local solution
            ArrayList path = r.getpath(); // get back the sequence of
                                                   // cities (path for this
                                                   // route)
            prevcity = 0;
            for (i = 1; i < path.size(); i++) {
              city = path.get(i);
              userParam.edges[prevcity][city] += r.getQ(); // convert into edges
              prevcity = city;
            }
          }
        }

        // find a fractional edge
        for (i = 0; i < userParam.nbclients + 2; i++) {
          for (j = 0; j < userParam.nbclients + 2; j++) {
            coef = userParam.edges[i][j];
            if ((coef > 1e-6)
                && ((coef < 0.9999999999) || (coef > 1.0000000001))) {
              // this route has a fractional coefficient in the solution =>
              // should we branch on this one?
              feasible = false;
              // what if we impose this route in the solution? Q=1
              // keep the ref of the edge which should lead to the largest
              // change
              change = (coef < Math.abs(1.0 - coef)) ? coef : Math.abs(1.0 - coef);
              change *= routes.get(i).getcost();
              if (change > bestObj) {
                bestEdge1 = i;
                bestEdge2 = j;
                bestObj = change;
                bestVal = (Math.abs(1.0 - coef) > coef) ? 0 : 1;
              }
            }
          }
        }
        CG = null;

        if (feasible) {
          if (branching.lowestValue < upperbound) { // new incumbant feasible solution!
            upperbound = branching.lowestValue;
            bestRoutes.clear();
            for (route r : routes) {
              if (r.getQ() > 1e-6) {
                route optim = new route();
                optim.setcost(r.getcost());
                optim.path = r.getpath();
                optim.setQ(r.getQ());
                bestRoutes.add(optim);
              }
            }
            System.out.println("OPT | Lower bound: " + lowerbound
                + " | Upper bound: " + upperbound + " | Gap: "
                + ((upperbound - lowerbound) / upperbound) + " | BB Depth: "
                + depth + " | Local CG cost: " + CGobj + " | " + routes.size()
                + " routes");
            System.out.flush();
          } else
            System.out.println("FEAS | Lower bound: " + lowerbound
                + " | Upper bound: " + upperbound + " | Gap: "
                + ((upperbound - lowerbound) / upperbound) + " | BB Depth: "
                + depth + " | Local CG cost: " + CGobj + " | " + routes.size()
                + " routes");
          return feasible;
        } else {
          System.out.println("INTEG INFEAS | Lower bound: " + lowerbound
              + " | Upper bound: " + upperbound + " | Gap: "
              + ((upperbound - lowerbound) / upperbound) + " | BB Depth: "
              + depth + " | Local CG cost: " + CGobj + " | " + routes.size()
              + " routes");
          System.out.flush();
          // ///////////////////////////////////////////////////////////
          // branching (diving strategy)

          // first branch -> set edges[bestEdge1][bestEdge2]=0
          // record the branching information in a tree list
          treeBB newnode1 = new treeBB();
          newnode1.father = branching;
          newnode1.branchFrom = bestEdge1;
          newnode1.branchTo = bestEdge2;
          newnode1.branchValue = bestVal; // first version was not with bestVal
                                          // but with 0
          newnode1.lowestValue = -1E10;
          newnode1.son0 = null;

          // branching on edges[bestEdge1][bestEdge2]=0
          EdgesBasedOnBranching(userParam, newnode1, false);

          // the initial lp for the CG contains all the routes of the previous
          // solution less the routes containing this arc
          ArrayList nodeRoutes = new ArrayList();
          for (route r : routes) {
            ArrayList path = r.getpath();
            boolean accept = true;
            if (path.size() > 3) { // we must keep trivial routes
                                   // Depot-City-Depot in the set to ensure
                                   // feasibility of the CG
              prevcity = 0;
              for (j = 1; accept && (j < path.size()); j++) {
                city = path.get(j);
                if ((prevcity == bestEdge1) && (city == bestEdge2))
                  accept = false;
                prevcity = city;
              }
            }
            if (accept)
              nodeRoutes.add(r);
          }

          boolean ok;
          ok = BBnode(userParam, nodeRoutes, newnode1, bestRoutes, depth + 1);
          nodeRoutes = null; // free memory
          if (!ok) {
            return false;
          }

          branching.son0 = newnode1;

          // second branch -> set edges[bestEdge1][bestEdge2]=1
          // record the branching information in a tree list
          treeBB newnode2 = new treeBB();
          newnode2.father = branching;
          newnode2.branchFrom = bestEdge1;
          newnode2.branchTo = bestEdge2;
          newnode2.branchValue = 1 - bestVal; // first version: always 1
          newnode2.lowestValue = -1E10;
          newnode2.son0 = null;

          // branching on edges[bestEdge1][bestEdge2]=1
          // second branching=>need to reinitialize the dist matrix
          for (i = 0; i < userParam.nbclients + 2; i++)
            System.arraycopy(userParam.distBase[i], 0, userParam.dist[i], 0,
                userParam.nbclients + 2);
          EdgesBasedOnBranching(userParam, newnode2, true);
          // the initial lp for the CG contains all the routes of the previous
          // solution less the routes incompatible with this arc
          ArrayList nodeRoutes2 = new ArrayList();
          for (route r : routes) {
            ArrayList path = r.getpath();
            boolean accept = true;
            if (path.size() > 3) { // we must keep trivial routes
                                   // Depot-City-Depot in the set to ensure
                                   // feasibility of the CG
              prevcity = 0;
              for (i = 1; accept && (i < path.size()); i++) {
                city = path.get(i);
                if (userParam.dist[prevcity][city] >= userParam.verybig - 1E-6)
                  accept = false;
                prevcity = city;
              }
            }
            if (accept)
              nodeRoutes2.add(r);

          }
          ok = BBnode(userParam, nodeRoutes2, newnode2, bestRoutes, depth + 1);
          nodeRoutes2 = null;

          // update lowest feasible value of this node
          branching.lowestValue = (newnode1.lowestValue < newnode2.lowestValue) ? newnode1.lowestValue
              : newnode2.lowestValue;

          return ok;

        }
      }

    } catch (IOException e) {
      System.err.println("Error: " + e);
    }
    return false;
  }

Column Generation的过程如下，Master Problem采用vrptw的set covering model 的松弛模型，利用cplex建模求解，求解的结果作为branch and bound的lower bound：

public double computeColGen(paramsVRP userParam, ArrayList routes)
      throws IOException {
    int i, j, prevcity, city;
    double cost, obj;
    double[] pi;
    boolean oncemore;

    try {

      // ---------------------------------------------------------
      // construct the model for the Restricted Master Problem
      // ---------------------------------------------------------
      // warning: for clarity, we create a new cplex env each time we start a
      // Column Generation
      // this class contains (nearly) everything about CG and could be used
      // independently
      // However, since the final goal is to encompass it inside 锟� Branch and
      // Bound (BB),
      // it would (probably) be better to create only once the CPlex env when we
      // initiate the BB and to work with the same (but adjusted) lp matrix each
      // time
      IloCplex cplex = new IloCplex();

      IloObjective objfunc = cplex.addMinimize();

      // for each vertex/client, one constraint (chapter 3, 3.23 )
      IloRange[] lpmatrix = new IloRange[userParam.nbclients];
      for (i = 0; i < userParam.nbclients; i++)
        lpmatrix[i] = cplex.addRange(1.0, Double.MAX_VALUE); 
      // for each constraint, right member >=1
      // lpmatrix[i] = cplex.addRange(1.0, 1.0); 
      // or for each constraint, right member=1 ... what is the best?

      // Declaration of the variables
      IloNumVarArray y = new IloNumVarArray(); // y_p to define whether a path p
                                               // is used

      // Populate the lp matrix and the objective function
      // first with the routes provided by the argument 'routes' of the function
      // (in the context of the Branch and Bound, it would be a pity to start
      // again the CG from scratch at each node of the BB!)
      // (we should reuse parts of the previous solution(s))
      for (route r : routes) {
        int v;
        cost = 0.0;
        prevcity = 0;
        for (i = 1; i < r.getpath().size(); i++) {
          city = r.getpath().get(i);
          cost += userParam.dist[prevcity][city];
          prevcity = city;
        }

        r.setcost(cost);
        IloColumn column = cplex.column(objfunc, r.getcost()); 
        // obj coefficient
        for (i = 1; i < r.getpath().size() - 1; i++) {
          v = r.getpath().get(i) - 1;
          column = column.and(cplex.column(lpmatrix[v], 1.0)); 
          // coefficient of y_i in (3.23) => 0 for the other y_p
        }
        y.add(cplex.numVar(column, 0.0, Double.MAX_VALUE)); 
        // creation of the variable y_i
      }
      // complete the lp with basic route to ensure feasibility
      if (routes.size() < userParam.nbclients) { // a priori true only the first time
        for (i = 0; i < userParam.nbclients; i++) {
          cost = userParam.dist[0][i + 1]
              + userParam.dist[i + 1][userParam.nbclients + 1];
          IloColumn column = cplex.column(objfunc, cost); // obj coefficient
          column = column.and(cplex.column(lpmatrix[i], 1.0)); // coefficient of
                                                               // y_i in (3.23)
                                                               // => 0 for the
                                                               // other y_p
          y.add(cplex.numVar(column, 0.0, Double.MAX_VALUE)); // creation of the
                                                              // variable y_i
          route newroute = new route();
          newroute.addcity(0);
          newroute.addcity(i + 1);
          newroute.addcity(userParam.nbclients + 1);
          newroute.setcost(cost);
          routes.add(newroute);
        }
      }

      // cplex.exportModel("model.lp");

      // CPlex params
      cplex.setParam(IloCplex.IntParam.RootAlg, IloCplex.Algorithm.Primal);
      cplex.setOut(null);
      // cplex.setParam(IloCplex.DoubleParam.TiLim,30); // max number of
      // seconds: 2h=7200 24h=86400

      // ---------------------------------------------------------
      // column generation process
      // ---------------------------------------------------------
      DecimalFormat df = new DecimalFormat("#0000.00");
      oncemore = true;
      double[] prevobj = new double[100];
      int nbroute;
      int previ = -1;
      while (oncemore) {

        oncemore = false;
        // ---------------------------------------s------------------
        // solve the current RMP
        // ---------------------------------------------------------
        if (!cplex.solve()) {
          System.out.println("CG: relaxation infeasible!");
          return 1E10;
        }
        prevobj[(++previ) % 100] = cplex.getObjValue();
        // store the 30 last obj values to check stability afterwards

        // System.out.println(cplex.getStatus());
        // cplex.exportModel("model.lp");

        // ---------------------------------------------------------
        // solve the subproblem to find new columns (if any)
        // ---------------------------------------------------------
        // first define the new costs for the subproblem objective function
        // (SPPRC)
        pi = cplex.getDuals(lpmatrix);
        for (i = 1; i < userParam.nbclients + 1; i++)
          for (j = 0; j < userParam.nbclients + 2; j++)
            userParam.cost[i][j] = userParam.dist[i][j] - pi[i - 1];

        // start dynamic programming
        SPPRC sp = new SPPRC();
        ArrayList routesSPPRC = new ArrayList();

        nbroute = userParam.nbclients; // arbitrarily limit to the 5 first
                                       // shortest paths with negative cost
        // if ((previ>100) &&
        // (prevobj[(previ-3)%100]-prevobj[previ%100]<0.0003*Math.abs((prevobj[(previ-99)%100]-prevobj[previ%100]))))
        // {
        // System.out.print("/");
        // complete=true; // it the convergence is too slow, start a "complete"
        // shortestpast
        // }
        sp.shortestPath(userParam, routesSPPRC, nbroute);
        sp = null;

        // /////////////////////////////
        // parameter here
        if (routesSPPRC.size() > 0) {
          for (route r : routesSPPRC) {
//             if (userParam.debug) {
//             System.out.println(" "+r.getcost());
//             }
            ArrayList rout = r.getpath();
            prevcity = rout.get(1);
            cost = userParam.dist[0][prevcity];
            IloColumn column = cplex.column(lpmatrix[rout.get(1) - 1], 1.0);
            for (i = 2; i < rout.size() - 1; i++) {
              city = rout.get(i);
              cost += userParam.dist[prevcity][city];
              prevcity = city;
              column = column.and(cplex.column(lpmatrix[rout.get(i) - 1], 1.0)); 
              // coefficient of y_i in (3.23) => 0 for the other y_p
            }
            cost += userParam.dist[prevcity][userParam.nbclients + 1];
            column = column.and(cplex.column(objfunc, cost));
            y.add(cplex.numVar(column, 0.0, Double.MAX_VALUE,
                "P" + routes.size())); // creation of the variable y_i
            r.setcost(cost);
            routes.add(r);

            oncemore = true;
          }
          System.out.print("\nCG Iter " + previ + " Current cost: "
                  + df.format(prevobj[previ % 100]) + " " + routes.size()
                  + " routes");
            System.out.flush();
        }
        //if (previ % 50 == 0)
        routesSPPRC = null;
      }

      System.out.println();

      for (i = 0; i < y.getSize(); i++)
        routes.get(i).setQ(cplex.getValue(y.getElement(i)));
      obj = cplex.getObjValue(); // mmmmhhh: to check. To be entirely safe, we
                                 // should recompute the obj using the distBase
                                 // matrix instead of the dist matrix

      cplex.end();
      return obj;
    } catch (IloException e) {
      System.err.println("Concert exception caught '" + e + "' caught");
    }
    return 1E10;
  }

ESPPRC的算法如下，采用label setting算法，感觉速度还可以，具体原理参照往期推文：

  public void shortestPath(paramsVRP userParamArg, ArrayList routes,int nbroute) {
    label current;
    int i,j,idx,nbsol,maxsol;
    double d,d2;
    int[]  checkDom;
    float tt,tt2;
    Integer currentidx;

    this.userParam=userParamArg;
    // unprocessed labels list => ordered TreeSet List (?optimal:  need to be sorted like this?)
    TreeSet U = new TreeSet(new MyLabelComparator());   // unprocessed labels list

    // processed labels list => ordered TreeSet List 
    TreeSet P = new TreeSet(new MyLabelComparator());   // unprocessed labels list

    // array of labels
    labels = new ArrayList(2*userParam.nbclients); // initial size at least larger than nb clients
    boolean[] cust= new boolean[userParam.nbclients+2];
    cust[0]=true;
    for (i=1;i[] city2labels = new ArrayList[userParam.nbclients+2];
    for (i=0;i();
      checkDom[i]=0;  // index of the first label in city2labels that needs to be checked for dominance (last labels added)
    }
    city2labels[0].add(0);

    nbsol = 0;
    maxsol = 2 * nbroute;
    while ((U.size()>0) && (nbsolwe'll keep the most negative ones
      // this is something to analyze further!  how many solutions to keep and which ones?
      // process one label => get the index AND remove it from U
      currentidx = U.pollFirst();
      current = labels.get(currentidx);

      // check for dominance
      // code not fully optimized: 
      int l1,l2;
      boolean pathdom;
      label la1,la2;
      ArrayList cleaning = new ArrayList();
      for (i = checkDom[current.city]; i < city2labels[current.city].size(); i++) {  // check for dominance between the labels added since the last time we came here with this city and all the other ones
        for (j = 0; j < i; j++) {
          l1 = city2labels[current.city].get(i);
          l2 = city2labels[current.city].get(j);
          la1 = labels.get(l1);
          la2 = labels.get(l2);
          if (!(la1.dominated || la2.dominated)) {  // could happen since we clean 'city2labels' thanks to 'cleaning' only after the double loop
            pathdom = true;
            for (int k = 1; pathdom && (k < userParam.nbclients+2); k++) 
              pathdom=(!la1.vertexVisited[k] || la2.vertexVisited[k]);
            if (pathdom && (la1.cost<=la2.cost) && (la1.ttime<=la2.ttime) && (la1.demand<=la2.demand)) {
              labels.get(l2).dominated = true;
              U.remove((Integer) l2);
              cleaning.add(l2);
              pathdom = false;
              //System.out.print(" ###Remove"+l2);
            } 
            pathdom = true;
            for (int k = 1; pathdom && (k < userParam.nbclients + 2); k++) 
              pathdom = (!la2.vertexVisited[k] || la1.vertexVisited[k]);

            if (pathdom && (la2.cost<=la1.cost) && (la2.ttime<=la1.ttime) && (la2.demand<=la1.demand)) {
              labels.get(l1).dominated = true;
              U.remove(l1);
              cleaning.add(l1);
              //System.out.print(" ###Remove"+l1);
              j = city2labels[current.city].size();
            }
          }
        }
      }

      for (Integer c : cleaning) 
        city2labels[current.city].remove((Integer) c);   // a little bit confusing but ok since c is an Integer and not an int!

      cleaning = null;
      checkDom[current.city] = city2labels[current.city].size();  // update checkDom: all labels currently in city2labels were checked for dom.

      // expand REF
      if (!current.dominated){ 
        //System.out.println("Label "+current.city+" "+current.indexPrevLabel+" "+current.cost+" "+current.ttime+" "+current.dominated);
        if (current.city == userParam.nbclients + 1) { // shortest path candidate to the depot!
          if (current.cost<-1e-7)  {        // SP candidate for the column generation
            P.add(currentidx);
            nbsol=0;
            for (Integer labi : P) {
              label s = labels.get(labi);
              if (!s.dominated)
                nbsol++;
            }
          }
        } else {  // if not the depot, we can consider extensions of the path
          for (i = 0; i < userParam.nbclients + 2; i++) {
            if ((!current.vertexVisited[i]) && (userParam.dist[current.city][i] < userParam.verybig-1e-6)) {  // don't go back to a vertex already visited or along a forbidden edge
              // ttime
              tt = (float) (current.ttime + userParam.ttime[current.city][i] + userParam.s[current.city]);
              if (tt < userParam.a[i])
                tt = userParam.a[i];
              // demand
              d = current.demand + userParam.d[i];
              //System.out.println("  -- "+i+" d:"+d+" t:"+tt);

              // is feasible?
              if ((tt <= userParam.b[i]) && (d <= userParam.capacity)) {
                idx = labels.size();
                boolean[] newcust = new boolean[userParam.nbclients + 2];
                System.arraycopy(current.vertexVisited, 0, newcust, 0, userParam.nbclients + 2);
                newcust[i] = true;
                //speedup: third technique - Feillet 2004 as mentioned in Laporte's paper
                for (j=1;j<=userParam.nbclients;j++)
                  if (!newcust[j]) {
                    tt2=(float) (tt+userParam.ttime[i][j]+userParam.s[i]);
                    d2=d+userParam.d[j];
                    if ((tt2>userParam.b[j]) || (d2>userParam.capacity))
                      newcust[j]=true;  // useless to visit this client
                  }

                labels.add(new label(i, currentidx, current.cost+userParam.cost[current.city][i], tt, d, false, newcust));  // first label: start from depot (client 0)
                if (!U.add((Integer) idx)) {  
                  // only happens if there exists already a label at this vertex with the same cost, time and demand and visiting the same cities before
                  // It can happen with some paths where the order of the cities is permuted
                  labels.get(idx).dominated = true; // => we can forget this label and keep only the other one
                } else 
                  city2labels[i].add(idx);

              }
            }
          }
        }
      }
    }
    // clean
    checkDom = null;

    // filtering: find the path from depot to the destination
    Integer lab;
    i = 0;
    while ((i < nbroute) && ((lab = P.pollFirst()) != null)) {
      label s = labels.get(lab);
      if (!s.dominated) {
        if (/*(i < nbroute / 2) ||*/ (s.cost < -1e-4)) {
          // System.out.println(s.cost);
//          if(s.cost > 0) {
//            System.out.println("warning >>>>>>>>>>>>>>>>>>>>");
//          }
          route newroute = new route();
          newroute.setcost(s.cost);
          newroute.addcity(s.city);
          int path = s.indexPrevLabel;
          while (path >= 0) {
            newroute.addcity(labels.get(path).city);
            path = labels.get(path).indexPrevLabel;
          }
          newroute.switchpath();
          routes.add(newroute);
          i++;
        }
      }

    }
  }

没想到吧，一个算法就包含了这么多知识点，没点基础真的是搞不定的哦~

大家好好加油吧哈哈。

【如对代码有疑问，可联系小编，可以提供有偿辅导服务】