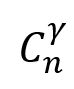R-第8天

1、table函数频数统计

注意路径是双斜线 \\

#读入csv文件

read.csv(file = "E:\\files\\DT\\BF\\R语言\\R第8天\\drink.csv",
         header = T)

#读入.data文件
dr<-scan("E:\\files\\DT\\BF\\R语言\\R第8天\\drink.data",
        what = list(gender="",type=""))
scan按照行进行扫描

 

#一维结构是频数表
#二维结构是交叉列联表
table(dr)

table(dr$gender)

table(dr$type)
Ta<-table(dr)

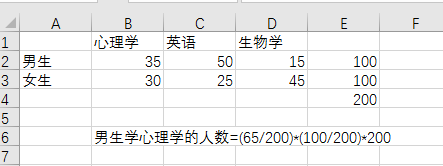
 计算边缘表

#计算边缘表
#1代表行维度，2代表列维度
margin.table(Ta,1)
margin.table(Ta,2)

#计算总频数
margin.table(Ta,)
margin.table(Ta,NULL)

#计算频率
prop.table(Ta)*100
prop.table(Ta,1)*100
prop.table(Ta,2)*100

 分箱（分组）操作

#读取birth.data数据
bir<-scan("E:\\files\\DT\\BF\\R语言\\R第8天\\birth.data")

table(bir)
#分箱操作(分组)
#分成5组
cut(bir,breaks = 5)
# 把克换成斤 
bir<-bir/500
# 1,2,3指 几斤
b<-c(-Inf,1,2,3,4,5,6,7,8,9,Inf)
cut(bir,breaks = b)
table(cut(bir,breaks = b))
# 再次划分区间
breakss<-c(0,4,8,Inf)
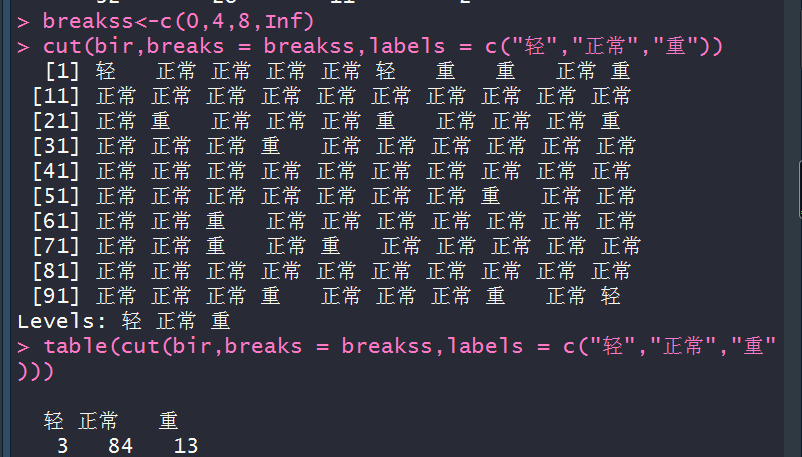
cut(bir,breaks = breakss,labels = c("轻","正常","重"))
table(cut(bir,breaks = breakss,labels = c("轻","正常","重")))

 

 

#读取.RData数据
load("E:\\files\\DT\\BF\\R语言\\R第8天\\物业改革支持度调查数据.RData")

ls()
table(wygg$性别,wygg$态度)

#计算汇总数据
addmargins(table(wygg$性别,wygg$态度))

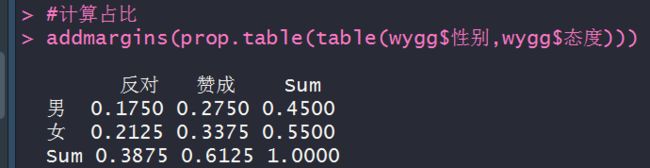
#计算占比
addmargins(prop.table(table(wygg$性别,wygg$态度)))

table(wygg)
ftable(wygg)

#指定行列变量
ftable(wygg,row.vars = c("性别","态度"),col.vars = "社区")
ftable(addmargins(table(wygg)))

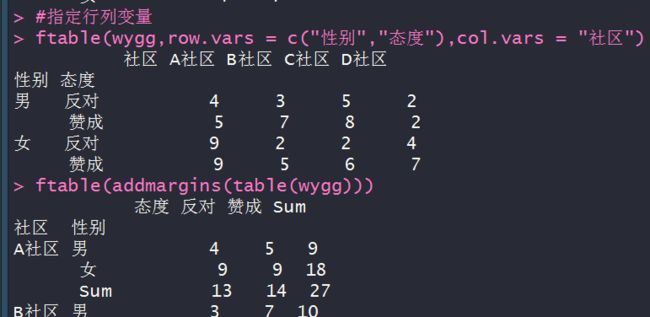
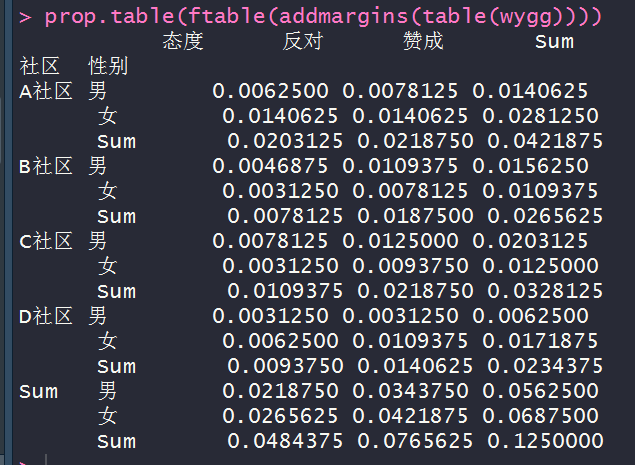
prop.table(ftable(addmargins(table(wygg))))

卡方分布-两个分类变量的相关性

检验独立性

 

 

 

 

 

 

 先复制，数据在剪切板里面

#卡方分布
# 读取剪切板

n_z<-read.table("clipboard")
class(n_z)
chisq.test(n_z)


不相关的概率小于0.05所以拒绝零假设
p-value<0.05,

统计上存在显著差异，拒绝零假设，从而验证两个分类变量具有相关性。

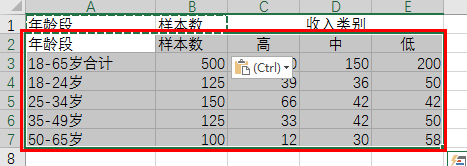
剖面指数分析

分析，哪一类客户才是我们产品的主要使用者

#剖面指数分析
#剖面指数：子市场与总市场的结构的对比
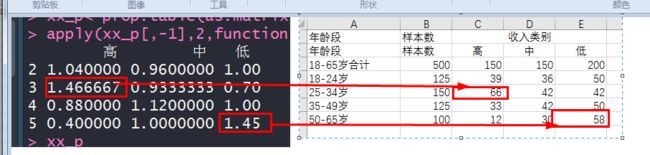
#如果剖面指数>1.2，则认为子市场是高于市场总体水平的，
#如果剖面指数<0.8,则认为子市场是低于市场总体水平的，
#如果剖面指数在0.8~1.2之间，则认为子市场与总市场没有差异

 

 

# T = TRUE
x_r<-read.table("clipboard",header = T)

# 转置矩阵
xx_p<-prop.table(as.matrix(x_r[-1,-1]),2)

apply(xx_p[,-1],2,function(x) x/xx_p[,1])

 主要的客户群体

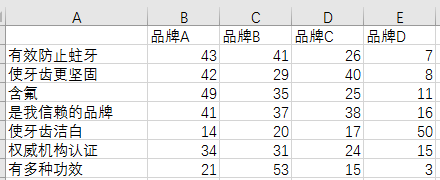
 期望值-观察值分析

 

 

 

#期望值-观察值分析
xy<-read.table("clipboard")

#计算列平均
xy_c<-colMeans(xy)

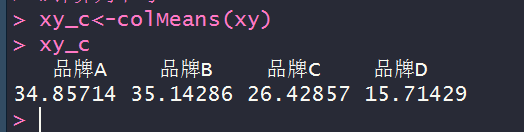
apply(xy,2,mean)
# 求列平均的两种方法

#计算行平均
xy_r<-rowMeans(xy)

#计算总平均
z_m<-mean(as.matrix(xy))

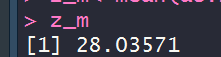
#计算期望值
# A%o%B运算，就是把A矩阵中所有元素，分别扩大B中元素的倍数。
r_c<-(xy_r %o% xy_c)/z_m

#实际值-期望值
xxtz<-xy-r_c

 

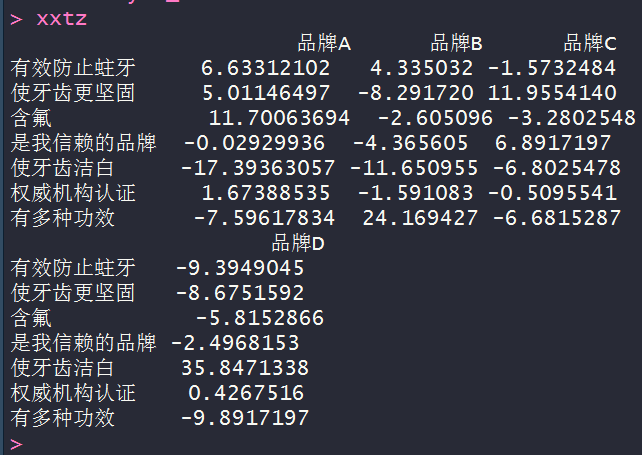
which.max(xxtz$品牌A)
row.names(xxtz)[3]
row.names(xxtz)[which.max(xxtz$品牌A)]
sapply(xxtz,function(x) row.names(xxtz)[which.max(x)])

 #编写程序计算 h(x,n)=1+x+x^2+……+x^n

xx7<-function(x,n){
  h<-1
  for (i in 1:n) {
    h<-h+x^i
  }
  h
}
xx7(x=2,n=5)

编写n中选r的组合函数，即 。

 

xx9<-function(n,r){
  a<-prod(1:n)
  b<-(prod(1:r))*(prod(1:(n-r)))
  return(a/b)
}
xx9(5,4)
prod(1:3)

 

111