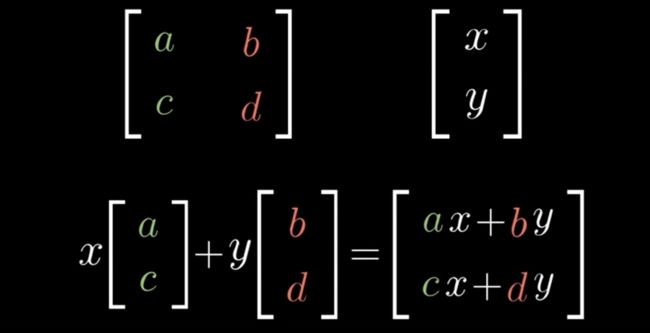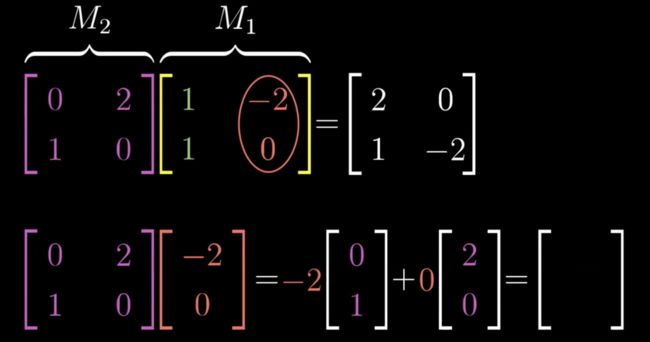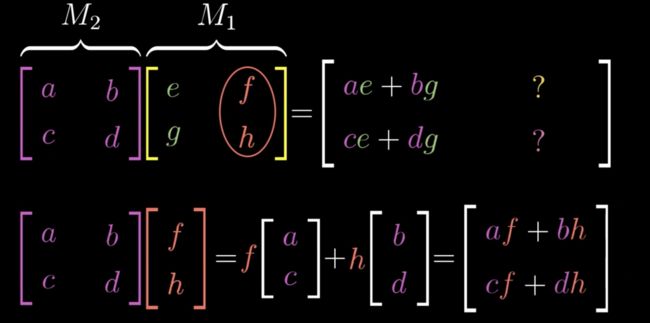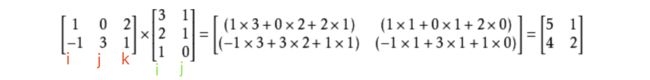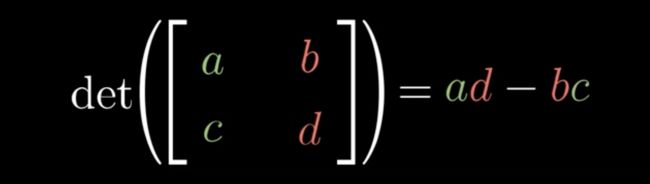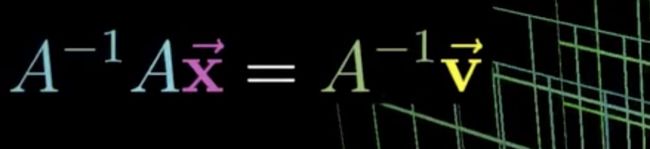线性代数的本质
一、向量究竟是什么?
计算机人眼中,矩阵不过是一种数据结构,比如记录一片地区的房屋价格,就可以用矩阵表示,实际上也是一种二维向量(其实更深入的探讨,矩阵可以理解为函数)
二、线性组合、张成的空间与基
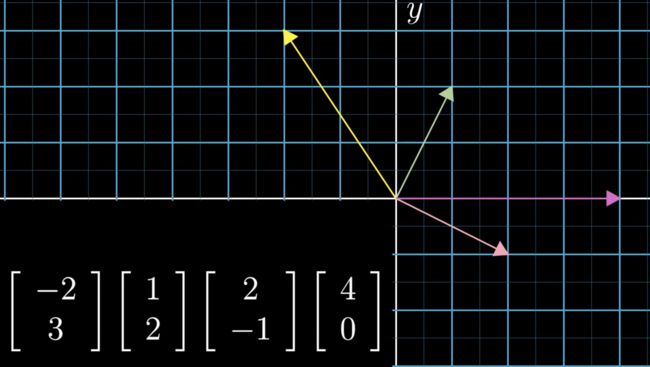
上一节聊过,矩阵不过是一种向量,我们的向量可以由基向量 i、j 转换而来,那么 ,我可以通过向量就能描述一个所有的二维空间,这样对于计算来说,太繁琐了 。
我们简化一下,用向量的终点表示向量,即一个点,这些点在坐标系上形成了无数矩阵化的点。
三、矩阵与线性变换
如果一种变换满足以下两种条件:1、直线在变换后还是直线,不能弯曲;2、原点保持不变 ,那么就称为 线性变换
我们知道,向量就是矩阵,那么空间中的任意一个向量就 该等于它们的基向量的线性变换,也就是一个向量V,可以表示为 v = ai + bj
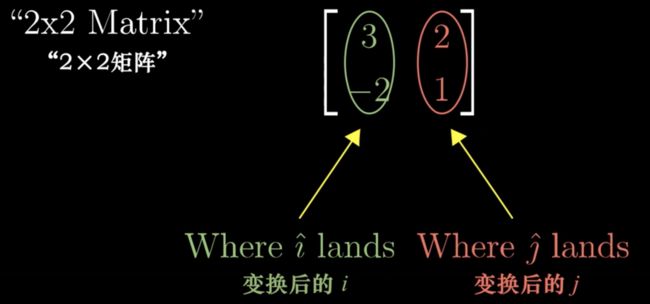
如图,我们知道任意的i和j,就能推算出来变换后的新矩阵,xy的原基向量不用管,基向量单位为1,那么x和y就是对应的i 和j 的倍数
把i和j放在一起,组成2*2矩阵,矩阵就是这么组合方式
如图,xy矩阵按 abcd 线性变换会得到什么?实际上,可以理解为xy 这个向量按照 ac bd作为的基向量 变换,,得出线性变换的结果,简单易懂,轻松理解乘法,不用死记硬背(以上属于线性变换)
上图的意义是什么?上图中 ac 和 bd 可以当成是线性变换后的 i、j基向量,我们不用管之前的xy基向量是啥,只知道之前的基向量下的某个向量值为 xy (没法按矩阵竖着写出来,用横着写默认表示竖着写的矩阵) ,之前的基向量线性变换后成了新的基向量 ac 和 bd,那么原来的xy线性变换后的新的x y是什么?就是上图的表达式:二者的乘积。
矩阵的乘法的意义就是表示了空间向量的线性变换,要求相乘 的两个矩阵左边的列和右边的行相同的。
四、矩阵乘法与线性变换复合
上节我们提到一个 2*2 的矩阵乘以 1*2 矩阵,那么 对于 2*2的两个矩阵相乘,它的意义是什么?
我们设想,对于一个1*2矩阵,我们不管它的初始i、j,我们记住它变换了一次[abcd],再变换一次[efgh],那么这个矩阵会变成什么样子?
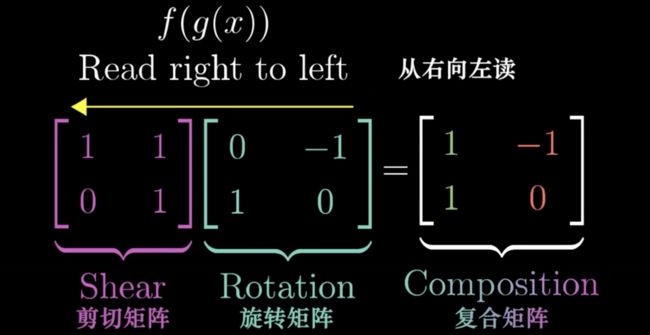
一个任意的向量,经过一次旋转动作,得出新的 i j,再经过一次剪切动作,得出i j,最后得出 新形成的复合 的 i j,约掉该任意向量,得出如图结果,注意这个过程可以看出函数f(g(x)),所以矩阵有严格顺序
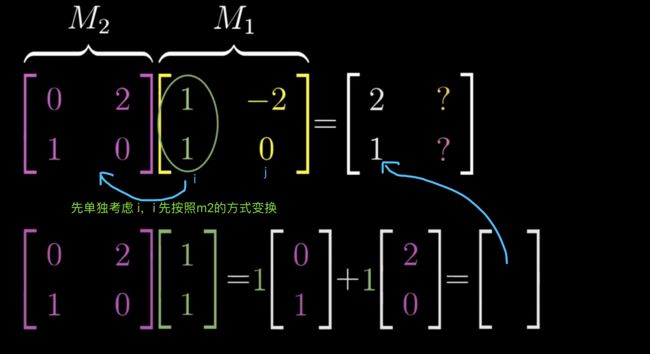
对于复合的线性变换,之前我们算过,[x,y] 可以约去,不用关心,那么我们只需关心复合变换后的各自 i、j,比如图中M1,我们可以把它拆解嘛,先看它的i经过M2变换后的得到的i,再看它的j经过M2变换后 得到的j(以上属于复合变换)
矩阵 AB ≠ BA
附录:三维空间的线性变换
三维空间的线性变换和第四节提到的一样,就是二维的维度多一次复合变换,可以拆解,从又往左看。
如图,从右往左看,绿字是三维矩阵,但它没有K分量,说白了它是原始XYZ矩阵变换后,有一维度没了,成了三维空间里的二维向量。红字矩阵实际上是也是三维空间的二维向量,它矩阵里没有Z轴 先拆解绿字矩阵,绿i要经过红字矩阵变换(实际也是通过红色向量ijk变换)后得出新矩阵(向量),计算的时候,先看绿i向量在红矩阵组合向量的变换下,最终得出什么样的向量,再看j向量在红矩阵组合向量下得出什么新向量,再把得到的新i新j一合组成新矩阵,就是我们要的结果,所以最终结果是2*2矩阵
(记住,不管红绿矩阵,它的里面参数都是有个原始矩阵,这个原始矩阵就是我们默认的是标准的三维空间坐标X、Y、Z它们对应的标准ijk帽。只不过在矩阵计算中,它左右约掉了,所以不用管,这里提到是为了便于理解这个矩阵乘法的意义,不然太抽象了)
五、行列式
什么是行列式? 百度的定位看起来很复杂,便于理解,我们可以先在一个二维空间画一块blob,这个区域实际上可以理解成矩阵,由很多小块矩阵各自拼接出来的。那么,现在我们进行线性变换,这个blob面积就会发生变化,行列式就是表示这个面积的缩放比例。在三维空间,即三阶矩阵中,行列式表示体积缩放的比例。
如图,det行列式如果结果是数字,表示缩放比例,结果是零,表示此时面积为0,或者是空间直线向量或者是点
那行列式的值如何计算?比如这个二阶矩阵,实际上就是i,j 两个向量嘛,i坐标x=a,y=c; j坐标x=b,y=d,那么它们和原始的i(x=1,y=0)j(x=0,y=1)相比,它们的放大比例就是 ad-bc
上面这段怎么理解?实际上就是两个i j 向量各自组成的面积块中,通过几何一算即得出 ad-bc 这样的公式。det就是对i j 的拉伸。
六、逆矩阵、列空间与零空间
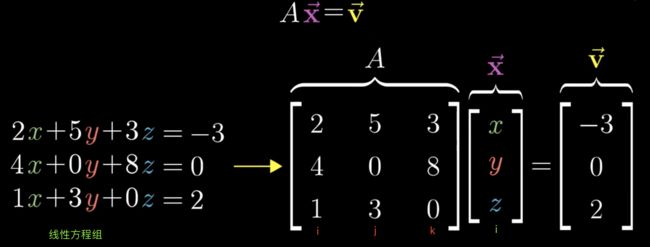
图左边,这样没有xy,没有x^2这种形式,只是乘法和加法,称为线性方程组,可以把这个方程组变成图右边的矩阵,红ijk三维空间只变化i,变成新的绿i,最后结果是一个三维空间的一维向量[-3 0 2],那如何求出这个x→ ?这就需要引入逆矩阵。
逆矩阵与矩阵可形象表述为倒带和正放,就是在空间中我反向向旋转一下,再正向旋转一下,最后的结果不变。记住矩阵乘法是在左边加新矩阵,从右往左算,如图,左边一逆一正等于1,什么也没有,那么求x→ 就变成了A逆和向量的乘积了
即使不存在逆运算(逆矩阵),也可能有解,比如说一个变换将空间压缩成直线,
秩:秩 精准定义是矩阵的列张成的空间 维度数。当秩与列数相同时候,我们成为满秩。注意定义里的张成二字,非满秩的情况下,比如虽然矩阵是2个列,但这个2个列正好在几何上处于一条直线,张成的是一条线,那实际上是一维,秩是1,就没满 。
当逆变换存在时,你能用逆变换求解方程组;否则,列空间的概念让我们理解什么时候存在解;零空间的概念有助于我们理解所有可能的解的集合是什么样子。
附录:非方阵
前面几章提到的矩阵,要么是二维到二维的变换,要么是三维到三维的变换,那么可否一个二维向量变成三维向量?
如图,这个矩阵的意义是什么?它的列只有i j,表面原矩阵一定是二维的,所以原矩阵通过如图矩阵变换时候,它只能是i j变换,但是ij里面又有了xyz三维的,该矩阵的意义为 二维空间映射到到三维空间,说直白点,这个矩阵,它是二维的,但它是三维空间中的二维平面
与上面相反,这个图的矩阵表示原向量是三维空间的,因为它有3列,有两行表示这个基向量在变换后变成二维空间,因此这是一个三维空间到二维空间的变换
七、点积与对偶性
注意,点积不是乘法,中间有个点哦,注意和矩阵乘法区别。矩阵乘法的要求是参与相乘的左矩阵的列数必须跟右矩阵的行数相同,即 A (M x N) 乘以 B (N x K) 的乘积矩阵C 为 M x K 维的。矩阵乘法结果矩阵的每个元素都是向量的内积,cij =
, 即A的第i行向量和B的第j列向量的内积。 矩阵点乘则要求参与运算的矩阵必须是相同维数的,是每个对应元素的逐个相乘。
点积百度百科-感觉解释的一般般
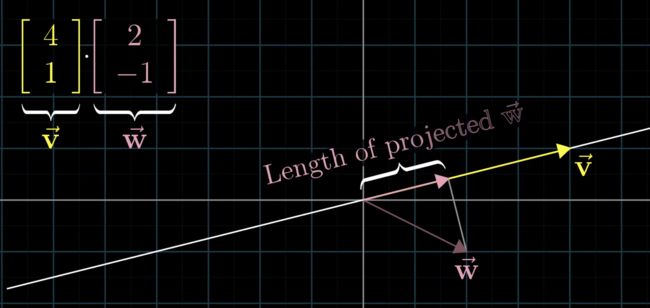
点积可以想象成投影,那么v*w其实是v在w上的投影与w相乘,当两者垂直,点积为0,两者放心相反,点积为负
如图,相当于w在v上的投影,将w投影的 长度与v相乘,就得出点积
点积可以干什么?两个向量的点积为正,表示朝向类似,为零,表示朝向垂直,为负,表示朝向相反。点积具有对偶性,v.w和w.v的结果是相同的,最终结果为实数。
前面,我们学了矩阵的乘法,那矩阵的点积和乘法到底啥区别?矩阵的乘法表示线性变换;而矩阵点积则是表示2个特殊向量的投影
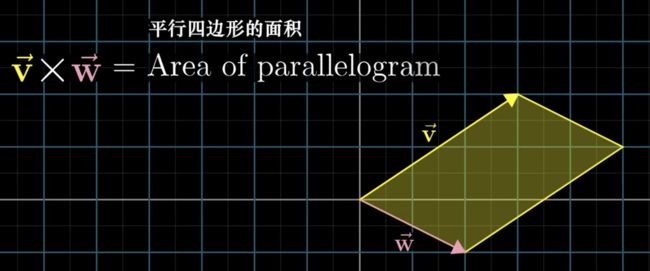
八、叉积的标准介绍
面积,就是叉积的意义,叉积是有顺序的,V✖️W= -W✖️V
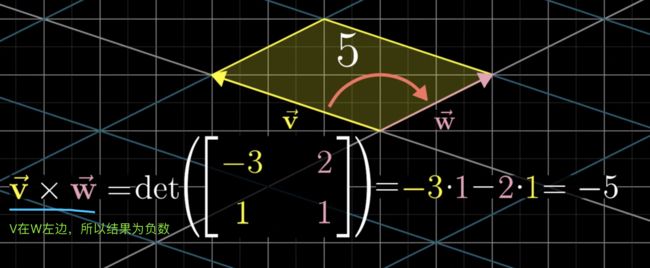
注意,叉积和前面的行列式对应上了。叉积的结果不是一个数,而是一个向量,这个向量垂直于张成的平面,长度是结果的数字,方向遵循右手定则。图中V是[-3 1],W是[2 1],求这个两个向量的叉积就等于求后面矩阵的行列式
九、基变换
如何在不同的坐标系之间切换?这里涉及到仿射变换。
矩阵乘法就是一个特殊的线性变换。比如,你当前坐标下有向量V ,为求空间扭转(也就是线性变换后)后的V的值,只需要知道空间扭转后的坐标系ij等,然后[ ]V 两者相乘即可得出V 变换 后新的坐标。
在你看到一个公式,是这样的格式:A逆 乘以 M 乘以 A,这按时熟悉上的转移作用。
相似矩阵。从右往左读,意义是某V向量,在A坐标系下是什么样子,然后通过M变换一下,再乘以A逆回到V原始的坐标系下。说白了是啥意思呢? 有个未知坐标系下的V 在已知的M坐标系下进行一次线性变换,变换后再倒腾会原始坐标系下,看看V此时状态下是什么值
十、特征向量与特征值
什么是特征向量?一个坐标系下的某向量,在该坐标系扭转后仍然方位不变,则称为该向量为特征向量。 用三维空间比较好了解,一块正方形,任意一条向量穿过正方形圆心,绕着该向量旋转放大,而该向量不动,则该向量为特征向量,或者说该向量是旋转轴。而这条向量放大缩小了多少,这个就是特征值。
有些矩阵没有特征向量,比如[1,0 0,1],它旋转90度后,所有向量都旋转了,没有向量保持不变,这种就没有特征向量。
如图为对角矩阵,什么是对角矩阵?就是假设一个矩阵,它的基向量就是特征向量,在几何中就是基向量可以伸缩或者为负反方向调整,这样,生成的一个新的坐标下,之前的基向量都是特征向量,它的特点就是对角线的数字对应着不同基向量的特征值,这个要结合视频更好 理解
一来一回,d就是b的对角矩阵,说白了某向量经过c变换后再经过b再逆矩阵a,得到的是一个基于b的基向量的矩阵,这个矩阵和 b 是对角矩阵
十一、线性代数的本质:抽象向量空间
矩阵可以理解为 函数。