一、概述
1、背景
最近几十年,人工智能经历了一轮又一轮的高潮和低谷;今天,机器学习、深度学习再一次被赋予强人工智能的历史使命;
机器学习作为人工智能中最重要的一环,天生就带有数学家和工程师的基因,了解机器学习的常见模型和算法还是很有意义的。
本文结合自己的学习情况介绍对线性回归模型的认识(如文章有不妥之处,望不吝赐教)
2、介绍
机器学习根据训练数据方法的不同,可以分为监督学习、半监督学习、无监督学习和强化学习。其中监督学习的主要任务是分类和回归
分类和回归问题都需要根据训练样本找到一个实数值函数g(x);然后回归根据g(x),可以推导出给定新样本的输出值,而分类是根据g(x),推导出新样本的类别(如0或1)。
在现实世界中普遍存在变量之间的关系,关系大概分两种:确定的函数关系 或 统计相关关系(非确定但又相互依赖的关系);回归分析就是研究变量之间统计相关关系的方法。
唯物辩证法中认为:事物之间的联系是普遍存在的、相互影响、相互作用和相互制约的;佛家认为:前世因,今世果;数学家认为: y = a_1x_1 + a_2x_2 + a_3x_3 + {\cdots}+ b
在回归问题中,按照自变量和变量之间的关系类型,分为线性回归分析和非线性回归分析(如对数模型:f(x) = \frac{1}{1+ e^{-x}}),本文介绍对象是线性回归(Linear Regression)模型。
3、线性回归模型
主要介绍:回归方程、损失函数、损失函数求解方法、过拟合和欠拟合、多项式
二、回归方程
1、概述
在回归分析中,只包括一个自变量和一个因变量,且两种的关系可以使用一条直线近似表示,称为一元线性回归分析。如果有两个及以上的自变量,且自变量和因变量是线性关系,称为多元线性回归分析。
一元线性回归方程: y = ax + b
多元线性回归方程: y = a_1x_1 + a_2x_2 + a_3x_3 + {\cdots} + b
2、建立回归方程
h_θ(x) = θ_0 + θ_1x_1+θ_2x_2+{\cdots}+θ_nx_n = \vec{θ}^T\vec{X}
其中,\vec{θ} = \begin{bmatrix} θ_0 \\ θ_1 \\ θ_2 \\ {\cdots} \\ θ_n \end{bmatrix} \,\,\,\,\,\,\vec{X} = \begin{bmatrix} 1 \\ x_1 \\ x_2 \\ {\cdots} \\ x_n \end{bmatrix}
说明:θ_0 , θ_1,θ_2,{\cdots}θ_n 是回归系数,我们的目标是求解出它们,然后代入回归方程,来预测新数据的输出值。
二、损失函数 (Loss Function)
1、公式
确立了回归方程后,我们使用均方误差(Mean Square Error,MSE)来评估真实值 与预测值之间的差异,公式如下:
J(θ) = \frac {1}{2n} \sum_{i=1}^n(h_θ(x^i) - y^i)^2,\,\,\text{n为样本数}
其矩阵表达式为:
J(θ) = \frac {1}{2n}(Xθ - Y)^T(Xθ - Y) ,\,\,\text{n为样本数}
说明:以上就是线性回归的损失函数。下面介绍公式的推导。
2、解释
- 假设特征的预测值和真实值的误差是\xi^{(i)} ,那么预测值θ^T x^{(i)}和真实值y^{(i)}满足如下公式:
y^{(i)} = θ^T x^{(i)} + \xi^{(i)}\,\,\,\,\,\,\,(1)
- 假设误差是独立的,随机的,无穷大的,根据中心极限定理,误差服从均值为\mu,方差为\sigma^2的正态分布,其概率分布如下:
p(\xi^{(i)}) = \frac {1}{\sqrt{2\pi\sigma}} exp(-\frac{{\xi^{(i)}}^2}{2\sigma^2})\,\,\,\,\,\,\,(2)
- 由公式(1)可知:\xi^{(i)} = y^{(i)} - θ^T x^{(i)},代入公式(2),得到一个y^{(i)}的概率公式如下:
p(y^{(i)} |x^{(i)};θ) = \frac {1}{\sqrt{2\pi} \sigma} exp(- \frac{(y^{(i)} - θ^T x^{(i)})^2}{2\sigma^2})\,\,\,\,\,\,\,(3)
- 对应的极大似然函数是:
L(θ) = \prod_{i=1}^np(y^{(i)} |x^{(i)};θ) = \prod_{i=1}^n\frac {1}{\sqrt{2\pi} \sigma} exp(- \frac{(y^{(i)} - θ^T x^{(i)})^2}{2\sigma^2})|x^{(i)};θ) \,\,\,\,\,\,\,(4)
- 极大似然函数取对数,求导后得到θ的极大似然估计如下
\hat{θ} = \frac {1}{2} \sum_{i=1}^n(h_θ(x^i) - y^i)^2 \,\,\,\,\,\,\,(5)
说明:极大似然函数估计知道,在\hat{θ} = \frac {1}{2} \sum_{i=1}^n(h_θ(x^i) - y^i)^2时,误差最小;为了后面计算推导,引入归一化的系数n, 最终得到的损失函数为:
J(θ) = \frac {1}{2n} \sum_{i=1}^n(h_θ(x^i) - y^i)^2,\,\,\text{n为样本数}
三、损失函数求解法1:普通最小二乘法(OLS)
1、求解
- 当矩阵X可逆时,可以用普通最小二乘法(OLS) ,求解出回归系数,公式如下(使用矩阵形式):
\hat{θ} = (X^TX)^{-1}X^TY
- 对应的代码实现如下:
def standRegre(xMat, yMat):
'''
:param xMat: X矩阵
:param yMat: y矩阵
:return: 回归系数矩阵
'''
xTx = xMat.T * xMat
# linalg.det(xTx)计算行列式,行列式值为0.矩阵不可逆
if linalg.det(xTx) == 0.0:
print("This matrix is singular,cannot do inverse")
return
# .I用作求矩阵的逆矩阵
ws = xTx.I * dot(xMat.T,yMat)
return ws
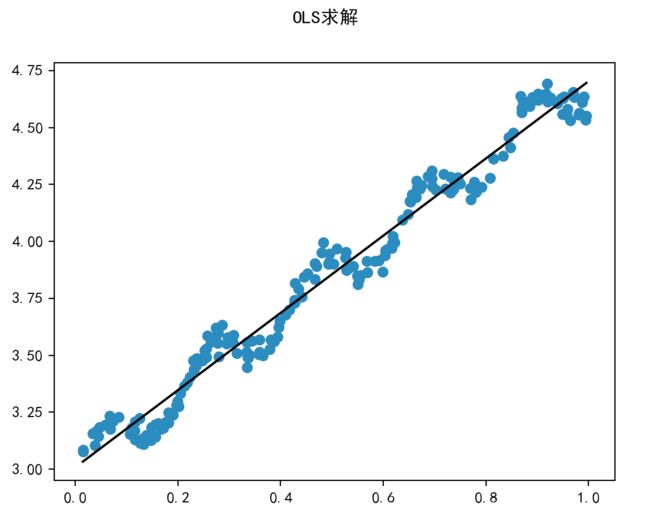
- 回归方程对数据点的拟合情况如下:
说明:要求矩阵X必须满足可逆条件,否则是不可以解的。
2、解释
我们知道,损失函数的矩阵表达式为
J(θ) = \frac {1}{2n}(Xθ - Y)^T(Xθ - Y)
扩展后得到:
J(θ) = \frac {1}{2n}(θ^TX^TXθ - 2θ^TX^TY + YY )
对θ求偏导,令导数为0,得:
\frac{\partial J(θ)}{\partial θ} = \frac {1}{2n}(2θ^TX^TX - 2X^TY) = 0
最后求解得到:
θ^T = (X^TX)^{-1}(X^TY)
四、损失函数求解法2:梯度下降(Gradient Descent)算法
1、 简介
梯度下降算法是一种求局部最优解的方法;在数学上,函数的梯度(导数)方向是函数值增长最快的方向,其相反方向就是下降最快的方向。
首先对\vec{θ}赋值,这个值可以是随机的,也可以是一个全零的向量。
改变\vec{θ}的值,使得J(θ)按梯度下降的方向进行减少。
θ = θ - \alpha \frac{\partial J(θ)}{\partial θ}, \,\,\, \alpha\text{是学习率,步长}
具体对θ的每个分量的求导公式如下:
\frac{\partial J(θ)}{\partial θ_j} = \frac{1}{n}\sum_{i=1}^n(h_θ(x^i) - y^i)x^i_j
说明:梯度下降(GD)是最小化损失函数的一种常用方法,主要有批量梯度下降和随机梯度下降两种迭代求解思路。
2、 批量梯度下降 (Batch Gradient Descent)
repeat until convergence {
\,\,\,\,\,\,\,\,\,θ_j:= θ_j - \alpha \frac{1}{n}\sum_{i=1}^n(h_θ(x^i) - y^i)x^i_j
}
说明:每更新一个θ_j ,都要遍历一次样本集;如果样本的数量n很大,开销比较大;BGD可以得到一个全局最优解,使得损失函数的风险最小
代码实现:
def bgd(rate, maxLoop, epsilon, X, Y):
'''
批量梯度下降法
:param rate: 学习率
:param maxLoop:
:param epsilon: 收敛精度
:param X: 样本特征矩阵
:param Y: 标签矩阵
:return: (theta, errors, thetas), timeConsumed
'''
# m是样本数,n是特征个数
m, n = X.shape
# 初始化theta,n*1维的零向量
theta = np.zeros((n, 1))
count = 0
# 是否收敛
converged = False
error = float('inf')
errors = []
thetas = {}
for j in range(n):
thetas[j] = [theta[j, 0]]
while count <= maxLoop:
if (converged):
break
count = count + 1
# sum = 0
for j in range(n):
# deriv = (X * theta - y).T * X[:, j] / m
# print(deriv)
deriv = np.float128(0)
for i in range(m):
deriv += ((X[i] * theta - Y[i]) * X[i,j])[0,0]/ m
theta[j, 0] = theta[j, 0] - rate * deriv
thetas[j].append(theta[j, 0])
#误差
error = loss_function(theta, X, y)
errors.append(error[0, 0])
# 如果已经收敛
if (error < epsilon):
converged = True
return theta, errors, thetas
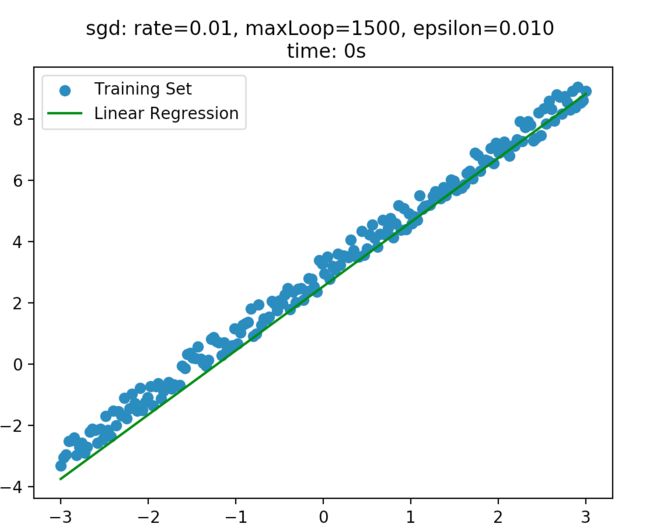
3、随机梯度下降 (Stochastic Gradient Descent)
repeat until convergence {
for i=1 to n {
\,\,\,\,\,\,\,\,θ_j:= θ_j - \alpha (h_θ(x^i) - y^i)x^i_j
}
}
说明1:在随机梯度下降法中,每更新θ_j 只需要一个样本 (x^i,y^i);在样本数量巨大时,SGD的性能比较好,但是最终结果未必是全局最优解。
代码实现
def sgd(rate, maxLoop, epsilon, dataMat, labelMat):
'''
随机梯度下降法
:param rate: 学习率
:param maxLoop:
:param epsilon: 收敛精度
:param dataMat: 样本特征矩阵
:param labelMat: 标签矩阵
'''
sampleCount, featureCount = dataMat.shape
#初始化theta,featureCount * 1维的0向量
theta = np.zeros((featureCount,1))
count = 0
converged = False
error = float('inf')
errors = []
thetas = {} #字典
for j in range(featureCount):
thetas[j] = [theta[j,0]]
# 迭代到最大次数结束
while count <= maxLoop:
if (converged):
break
count = count + 1
errors.append(float('inf'))
# 获取样本
for i in range(sampleCount):
if (converged):
break
#计算实际和预测的误差
diff = labelMat[i,0] - regression_function(theta,dataMat[i].T)
# 通过第i个样本来优化theta
for j in range(featureCount):
theta[j, 0] = theta[j, 0] + rate * diff * dataMat[i,j]
thetas[j].append(theta[j, 0])
error = loss_function(theta, dataMat, labelMat)
errors[-1] = error[0, 0]
# 如果已经收敛
if (error < epsilon):
converged = True
return theta, errors, thetas
4、其他
随机梯度下降法在还能够应用到一些更加复杂的算法中,如逻辑回归(Logic Regression)算法(虽有回归两字,但实际上是分类算法)等;
在回归模型的损失函数求解中,还有正规方程的方式,它不需要调节学习率\alpha,但是要求矩阵可逆,数据维度不能太大。
五、特征缩放
当样本的特征的数值之间差异比较大时,梯度下降的过程不仅曲折,而且耗时;这时候需要将各个特征归一化到统一的区间。常见的做法如下:
1、0均值标准化(Z-score normalization)
- 将原始数据集归一化为均值为0、方差为1的数据集,归一化后的特征将分布在 [−1,1] 区间,转化函数如下:
z=\frac {x - μ}{δ}
其中,μ、σ分别为原始数据集的均值和标准差。
说明:该种归一化方式要求原始数据的分布可以近似为高斯分布,否则归一化的效果会变得很糟糕。
- 代码实现如下:
def standardize(xArr):
'''
特征标准化处理
:param xArr: 样本特征集
:return: 标准化后的样本特征集
'''
m, n = xArr.shape
# 归一化每一个特征
for j in range(n):
meanVal = xArr[:, j].mean(axis=0)
std = xArr[:, j].std(axis=0)
if std != 0:
xArr[:, j] = (xArr[:, j] - meanVal) / pow(std,2)
else:
xArr[:, j] = 0
return xArr
2、线性函数归一化(Min-Max Scaling)
- 实现对原始数据的等比例缩放,将原始数据线性化的方法转换到[0,1]的范围,公式如下:
X_{normal} = \frac {X - X_{min}}{ X_{max} - X_{min}}
其中X_{norm}为归一化后的数据,X为原始数据,X_{max} 、X_{min}分别为原始数据集的最大值和最小值。
- 代码实现如下:
def normalize(xArr):
"""特征归一化处理
Args:
X: 样本特征集
Returns:
归一化后的样本特征集矩阵
"""
m, n = xArr.shape
# 归一化每一个特征
for j in range(n):
minVal = xArr[:, j].min(axis=0)
maxVal = xArr[:, j].max(axis=0)
diff = maxVal - minVal
if diff != 0:
xArr[:, j] = (xArr[:, j] - minVal) / diff
else:
xArr[:, j] = 0
return xArr
3、总结
在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,Z-score standardization表现更好。
在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用Min-Max Scaling或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
六、多项式回归
1、多项式
多项式由称为不定元的变量和常数系数通过有限次加减法、乘法以及自然数幂次的乘方运算得到的代数表达式,可以分为一次一元多项式和多元多项式。我们主要讨论一元多项式,其形式如下:
y = a_0 + a_1 * x + a_2 * (x^2) + ... + a_n * (x^n) + e
2、多项式回归
当回归函数不能用直线来描述时,要考虑用非线性回归函数。 多项式回归属于非线性回归的一种。这里主要介绍一元多项式回归。
一般非线性回归函数是未知的,或即使已知也未必可以用一个简单的函数变换转化为线性模型。常用的做法是用因子的多项式。
从散点图观察到回归函数有一个“弯”,则可考虑用二次多项式;有两个弯则考虑用三次多项式;有三个弯则考虑用四次多项式,等等。
真实的回归函数未必就是某个次数的多项式,但只要拟合得好,用适当的多项式来近似真实的回归函数是可行的。
七、拟合的问题
1、概念
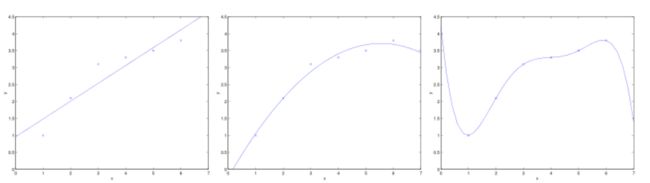
- 拟合:把平面上一系列的点,用一条光滑的曲线连接起来,拟合的曲线一般可以用函数表示,拟合曲线不是唯一的;在实践中,常常会出现过拟合和欠拟合问题;
最左边的直线没有很好拟合数据,这类情况是欠拟合(underfitting);最右边的曲线似乎对数据点做了很好的拟合(曲线通过了所有的点),但是它无法泛化到新的数据样本中,是一个差的模型,这种情况是过拟合的,只有中间的曲线才是理想的拟合曲线。
泛化指的是一个假设模型能够应用到新样本的能力。新样本数据是指没有出现在训练集中的数据。
特征过多 或者 样本量少的情况都容易发生过拟合的情况。解决的方法有两种:1)减少特征个数,选择最重要的特征,抛弃一部分特征;2)正则化,保留所有的特征,但是会减小特征变量的数量级。