Codeforces Round #615 (Div. 3) F. Three Paths on a Tree
题目链接:https://codeforces.com/contest/1294/problem/F
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given an unweighted tree with nn vertices. Recall that a tree is a connected undirected graph without cycles.
Your task is to choose three distinct vertices a,b,ca,b,c on this tree such that the number of edges which belong to at least one of the simple paths between aa and bb, bb and cc, or aa and cc is the maximum possible. See the notes section for a better understanding.
The simple path is the path that visits each vertex at most once.
Input
The first line contains one integer number nn (3≤n≤2⋅1053≤n≤2⋅105) — the number of vertices in the tree.
Next n−1n−1 lines describe the edges of the tree in form ai,biai,bi (1≤ai1≤ai, bi≤nbi≤n, ai≠biai≠bi). It is guaranteed that given graph is a tree.
Output
In the first line print one integer resres — the maximum number of edges which belong to at least one of the simple paths between aa and bb, bb and cc, or aa and cc.
In the second line print three integers a,b,ca,b,c such that 1≤a,b,c≤n1≤a,b,c≤n and a≠,b≠c,a≠ca≠,b≠c,a≠c.
If there are several answers, you can print any.
Example
input
Copy
8
1 2
2 3
3 4
4 5
4 6
3 7
3 8
output
Copy
5
1 8 6
Note
The picture corresponding to the first example (and another one correct answer):
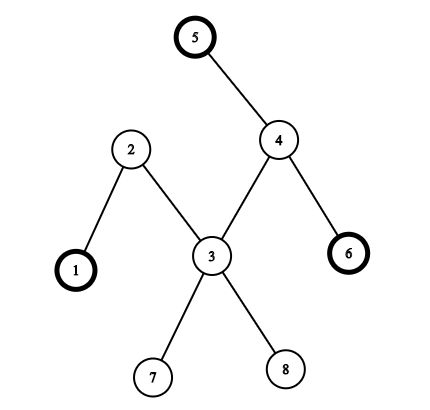
If you choose vertices 1,5,61,5,6 then the path between 11 and 55 consists of edges (1,2),(2,3),(3,4),(4,5)(1,2),(2,3),(3,4),(4,5), the path between 11 and 66 consists of edges (1,2),(2,3),(3,4),(4,6)(1,2),(2,3),(3,4),(4,6) and the path between 55 and 66 consists of edges (4,5),(4,6)(4,5),(4,6). The union of these paths is (1,2),(2,3),(3,4),(4,5),(4,6)(1,2),(2,3),(3,4),(4,5),(4,6) so the answer is 55. It can be shown that there is no better answer.
题意:
给定一个含有n个节点的无根树,让你选出3个节点a,b,c, 使3个节点之间的最短路径中的边数最多。
思路:
可以证明:这3个点中一定有两个点是这棵树直径的断点,比如说是a,b。
那么我们需要先通过找树的直径确定ab后再寻找到使答案尽可能大的c节点。
我们来分类讨论:(很重要!
①:树的直径长度为n-1,那么树就是一个链,我们C点只要选择不是ab点的任意一个其他节点即可。
②:树的直径长度小于n-1,那么把a节点到b节点以及a和b简单路径中节点缩成一个节点n+1,然后重新建树,寻找与n+1距离最远的那个节点c即可。树缩点的方法是:dfs时用栈维护路径中的节点即可。
如果不会求树的直径,可以去搜个靠谱的博客看一下。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
