【R语言学习笔记】 Day3 CART分类树、随机森林以及Boosting的应用及对比

1. 目的：根据银行客户信息，判断其是否接受银行向他们提供的个人贷款。

 

2. 数据来源：https://www.kaggle.com/lowecoryr/universalbank

 

3. 数据介绍：数据中共包含5000个观测值，14个变量。其中，每一个观测值代表一个客户。

bank.df <- read.csv("UniversalBank.csv") # 读取数据
str(bank.df) # 查看数据结构

 

 

View(bank.df) # 查看数据

 

 

4. 应用及分析

 

4.1 构建回归树模型

bank.df <- bank.df[ , -c(1, 5)] # 删除 ID 和 zip code 两列

# 将数据分为训练集和测试集
set.seed(1) 
train.index <- sample(c(1:dim(bank.df)[1]), dim(bank.df)[1]*0.6) 
train.df <- bank.df[train.index, ] # 训练集
valid.df <- bank.df[-train.index, ] # 测试集

# 运用训练集建立分类树模型
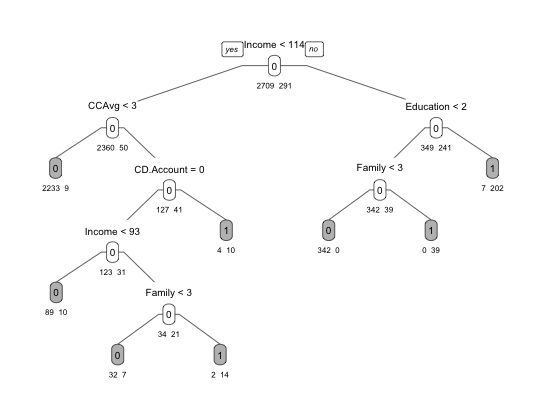
default.ct <- rpart(Personal.Loan ~ ., data = train.df, method = "class") # 没有设置cp或者depth，意味着建立一个有效的且尽可能简单的模型
prp(default.ct, type = 1, extra = 1, under = TRUE, split.font = 1, varlen = -10) 

 

library(caret) # 建立混淆矩阵
library(lattice)
library(ggplot2)


default.ct.point.pred.train <- predict(default.ct,train.df,type = "class") # 运用所建立的回归树模型预测训练集的数据
confusionMatrix(default.ct.point.pred.train, as.factor(train.df$Personal.Loan)) # 创建训练集数据与其预测结果的混淆矩阵

 

 

 

 将模型应用到训练集中，预测的准确性为98.7%。

 

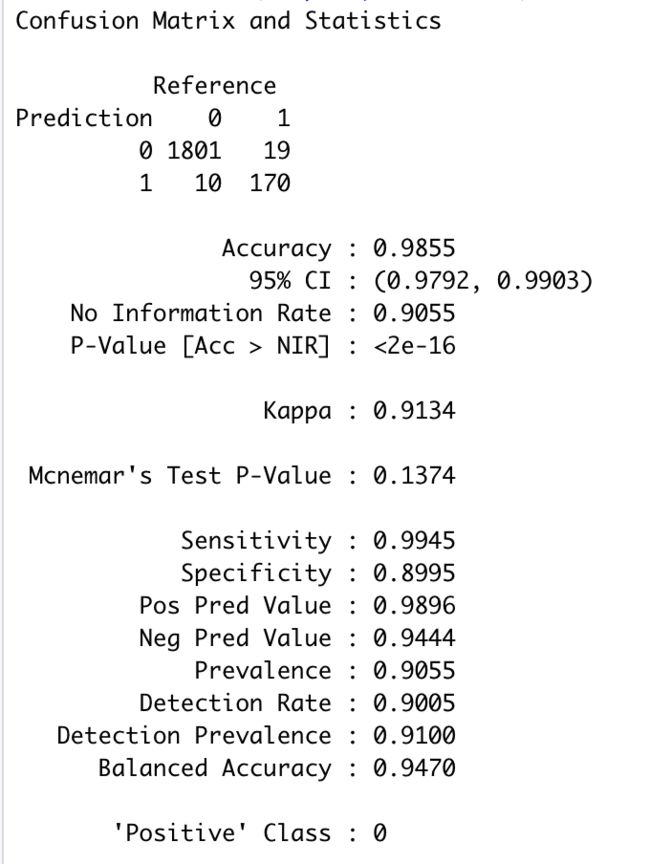
default.ct.point.pred.val <- predict(default.ct,valid.df,type = "class") # 运用所建立的回归树模型预测测试集的数据
confusionMatrix(default.ct.point.pred.val, as.factor(valid.df$Personal.Loan)) # 创建测试集数据与其预测结果的混淆矩阵

　　

 

 

 将模型应用到训练集中，预测的准确性为98.15%。

 

接下来，构建一个尽可能复杂的分类树模型。

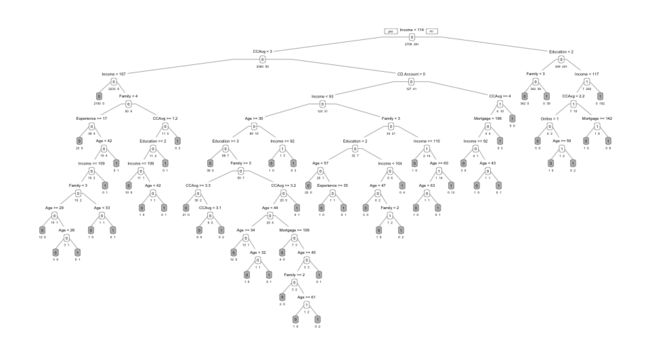
deeper.ct <- rpart(Personal.Loan ~ ., data = train.df, method = "class", cp = 0, minsplit = 1)
length(deeper.ct$frame$var[deeper.ct$frame$var == ""]) # 共有53个叶子
prp(deeper.ct, type = 1, extra = 1, under = TRUE, split.font = 1, varlen = -10, 
    box.col=ifelse(deeper.ct$frame$var == "", 'gray', 'white')) 

 

 

分类回归树模型一个很重要的优点在于简单、容易理解。但是，这个模型中的叶子多达53个，这使模型变得复杂很多。因此，接下来需要修剪如上分类树的叶子，来简化模型。

 

第一种修剪叶子的方法为找到最小的cost complexity所对应的cp值，并进行建模。

set.seed(1)
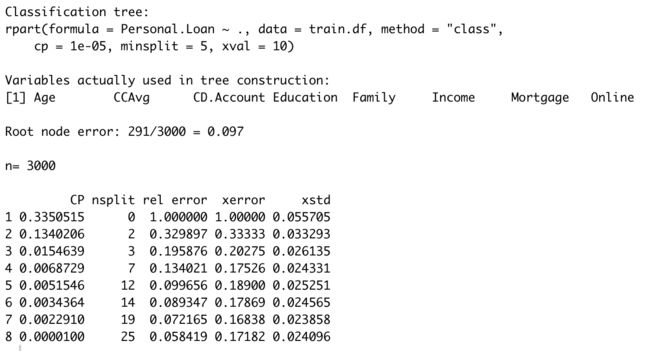
cv.ct <- rpart(Personal.Loan ~ ., data = train.df, method = "class", 
               cp = 0.00001, minsplit = 5, xval = 10)

# xval = 10 -代表交叉检验10次
# 交叉检验指的是不断将数据分为训练集和测试集，不断建立分类树模型，计算cost complexity，取使得cost complexity最小的cp值

printcp(cv.ct)

 

 

 

R语言中xerror代表cost complexity，因此，使得cost complexity最小的cp值为0.002291.

 

# 使用使得cost complexity最小的cp值来修剪树枝
pruned.ct <- prune(cv.ct, 
                   cp = cv.ct$cptable[which.min(cv.ct$cptable[,"xerror"]),"CP"])
length(pruned.ct$frame$var[pruned.ct$frame$var == ""]) # 新模型的叶子数为20
prp(pruned.ct, type = 1, extra = 1, split.font = 1, varlen = -10) 

 

 

但是，修剪叶子以后的模型仍包含较多的叶子，不是特别便于理解。因此，引入第二种修剪叶子的方法：使用cost complexity < 最小的cost complexity + std.dev的cp中，使得模型最简单的cp。

如上图所示，最小的cost complexity为0.16838，其所对应的std.dev为0.023858。因此最大可容忍的error为0.192238 ( = 0.16838 + 0.023858)。

当cp=0.0068729的时候，既满足xerror  < 0.192238，又满足最简单的模型。因此设置参数cp为0.0068729。

 

pruned.ct <- prune(cv.ct, cp = 0.0068729) 
prp(pruned.ct, type = 1, extra = 1, under = TRUE, split.font = 1, varlen = -10, 
    box.col=ifelse(pruned.ct$frame$var == "", 'gray', 'white')) 

 

 

 

 

4.2 构建随机森林模型

 

library(randomForest) # 加载randomForest包
rf <- randomForest(as.factor(Personal.Loan) ~ ., data = train.df,
                   ntree = 500, mtry = 4, nodesize = 5, importance = TRUE)
varImpPlot(rf, type = 1)

 

由此可见，Income, Education的平均基尼系数下降最多。

 

rf.pred <- predict(rf, valid.df) # 将随机森林模型应用到测试集并进行预测
confusionMatrix(rf.pred, as.factor(valid.df$Personal.Loan)) # 混淆矩阵

 

 

 

应用随机森林以后，模型应用于测试集的准确性由98.15%提高至98.55%。

 

# 绘制ROC曲线
library(pROC)
pl0 <- roc(valid.df$Personal.Loan, as.numeric(rf.pred))
plot(pl0, print.auc = T, auc.polygon = T, grid = c(0.1,0.2), grid.col=c("green", "red"), 
　　　　max.auc.polygon=TRUE, auc.polygon.col="skyblue", print.thres=TRUE, main='ROC Curve for Random Forest Algorithm')

 

 

 

 

 

 

4.3 构建boosted trees模型

library(adabag)
library(foreach)
library(doParallel)
library(iterators)
library(parallel)
library(rpart)
library(caret)

train.df$Personal.Loan <- as.factor(train.df$Personal.Loan) #将因变量转为factor类型变量

error <- as.numeric()

for (i in 1:20) {
  set.seed(1)
  boost <- boosting(Personal.Loan ~ ., data = train.df, boos = T, mfinal = i)
  pred <- predict(boost, valid.df)
  error[i] <- pred$error
}

# 用boosting()函数对训练集进行训练。
# 首先定义基分类器个数为1，通过循环依次增加基分类器个数，直至达到20。
# 基分类器个数通过boosting()中的mfinal参数进行设置。
# boos = T 代表权重使用迭代权重
# boos = F 代表各个观测使用相同的权重

library(ggplot2)
error <- as.data.frame(error) # 将error转变为data frame
p <- ggplot(error, aes(x = 1:20, y = error))  +
  geom_line(colour="red", linetype="dashed",size = 1) +
  geom_point(size = 3, shape = 18) + ylim(0,0.05) +
  xlab("the number of basic classifiers") + theme_bw() +
  theme(panel.grid = element_blank()) +
  theme(axis.title = element_text(face = 'bold'))
p 

 

 

因此，当弱学习机为数目为13的时候，误差最小。

 

boost <- boosting(Personal.Loan ~ ., data = train.df, boos = T, mfinal = 13) # 设置mfinal=13
pre <- predict(boost, newdata = valid.df)$class # pre是数值为0/1的变量
df <- data.frame(prob = pre, obs = valid.df$Personal.Loan)

# 混淆矩阵
t <- table(valid.df$Personal.Loan, pre, dnn = c('observed','predicted'))  # accuracy = (1805+176)/(1805+176+13+6)=99/05%

 

 

boosted trees 模型对测试集的预测准确性高达99.05%

 

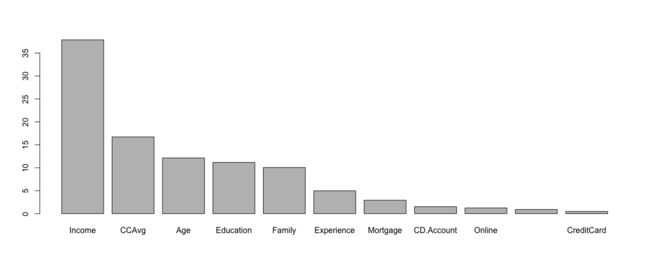
# 计算误差 = 0.0095
## method1
(sum(t) - sum(diag(t)))/sum(t) 
## method2
calculate error = predict(boost, newdata = valid.df)$error 


# 绘制各自变量的重要性
imp <- sort(boost$importance, decreasing = T) 
barplot(imp) 

 

 

# 绘制ROC曲线
library(pROC)
pl <- roc(valid.df$Personal.Loan, as.numeric(pre))
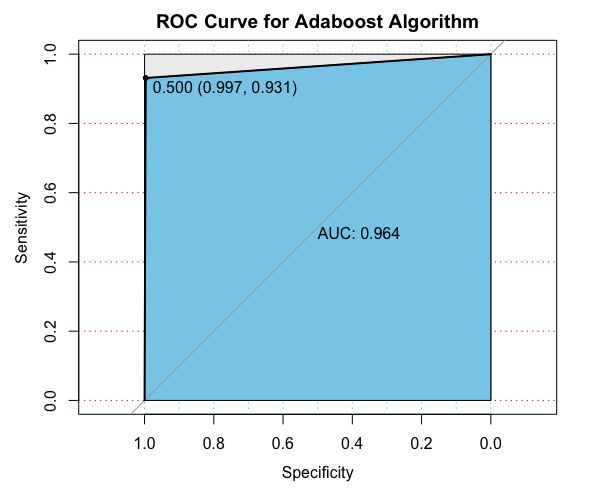
plot(pl, print.auc = T, auc.polygon = T, grid = c(0.1,0.2), grid.col=c("green", "red"), 
　　　　max.auc.polygon=TRUE, auc.polygon.col="skyblue", print.thres=TRUE, main='ROC Curve for Adaboost Algorithm')