the original page is sudoku|backtracking-7"
sudoku problem
Given a partially filled 9×9 2D array ‘grid[9][9]’, the goal is to assign digits (from 1 to 9) to the empty cells so that every row, column, and subgrid of size 3×3 contains exactly one instance of the digits from 1 to 9.
Naive Algorithm
The Naive Algorithm is to generate all possible configurations of numbers from 1 to 9 to fill the empty cells. Try every configuration one by one until the correct configuration is found.
Backtracking Algorithm
Like all other Backtracking problems, we can solve Sudoku by one by one assigning numbers to empty cells. Before assigning a number, we check whether it is safe to assign. We basically check that the same number is not present in the current row, current column and current 3X3 subgrid. After checking for safety, we assign the number, and recursively check whether this assignment leads to a solution or not. If the assignment doesn’t lead to a solution, then we try next number for the current empty cell. And if none of the number (1 to 9) leads to a solution, we return false.
Find row, col of an unassigned cell
If there is none, return true
For digits from 1 to 9
a) If there is no conflict for digit at row, col
assign digit to row, col and recursively try fill in rest of grid
b) If recursion successful, return true
c) Else, remove digit and try another
If all digits have been tried and nothing worked, return false
python implementaion
#!/usr/bin/env python3
# A Backtracking program in Pyhton to solve Sudoku problem
# A Utility Function to print the Grid
def print_grid(arr):
for i in range(9):
for j in range(9):
print(arr[i][j],end=' ')
print()
# Function to Find the entry in the Grid that is still not used
# Searches the grid to find an entry that is still unassigned. If
# found, the reference parameters row, col will be set the location
# that is unassigned, and true is returned. If no unassigned entries
# remain, false is returned.
# 'l' is a list variable that has been passed from the solve_sudoku function
# to keep track of incrementation of Rows and Columns
def find_empty_location(arr, l):
for row in range(9):
for col in range(9):
if(arr[row][col] == 0):
l[0] = row
l[1] = col
return True
return False
# Returns a boolean which indicates whether any assigned entry
# in the specified row matches the given number.
def used_in_row(arr, row, num):
for i in range(9):
if(arr[row][i] == num):
return True
return False
# Returns a boolean which indicates whether any assigned entry
# in the specified column matches the given number.
def used_in_col(arr, col, num):
for i in range(9):
if(arr[i][col] == num):
return True
return False
# Returns a boolean which indicates whether any assigned entry
# within the specified 3x3 box matches the given number
def used_in_box(arr, row, col, num):
for i in range(3):
for j in range(3):
if(arr[i+row][j+col] == num):
return True
return False
# Checks whether it will be legal to assign num to the given row,col
# Returns a boolean which indicates whether it will be legal to assign
# num to the given row,col location.
def check_location_is_safe(arr,row,col,num):
# Check if 'num' is not already placed in current row,
# current column and current 3x3 box
return not used_in_row(arr, row, num) and not used_in_col(arr, col, num) and not used_in_box(arr, row - row % 3, col - col % 3, num)
# Takes a partially filled-in grid and attempts to assign values to
# all unassigned locations in such a way to meet the requirements
# for Sudoku solution (non-duplication across rows, columns, and boxes)
def solve_sudoku(arr):
# 'l' is a list variable that keeps the record of row and col in find_empty_location Function
l = [0, 0]
# If there is no unassigned location, we are done
if(not find_empty_location(arr, l)):
return True
# Assigning list values to row and col that we got from the above Function
row = l[0]
col = l[1]
# consider digits 1 to 9
for num in range(1, 10):
# if looks promising
if(check_location_is_safe(arr, row, col, num)):
# make tentative assignment
arr[row][col] = num
# return, if sucess, ya!
if(solve_sudoku(arr)):
return True
# failure, unmake & try again
arr[row][col] = 0
# this triggers backtracking
return False # Driver main function to test above functions
if __name__ == "__main__":
# creating a 2D array for the grid
grid = [[0 for x in range(9)]for y in range(9)]
# assigning values to the grid
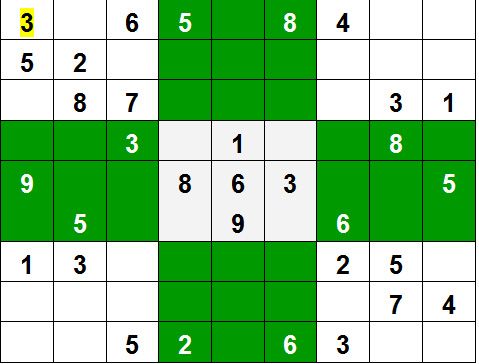
grid = [[3, 0, 6, 5, 0, 8, 4, 0, 0],
[5, 2, 0, 0, 0, 0, 0, 0, 0],
[0, 8, 7, 0, 0, 0, 0, 3, 1],
[0, 0, 3, 0, 1, 0, 0, 8, 0],
[9, 0, 0, 8, 6, 3, 0, 0, 5],
[0, 5, 0, 0, 9, 0, 6, 0, 0],
[1, 3, 0, 0, 0, 0, 2, 5, 0],
[0, 0, 0, 0, 0, 0, 0, 7, 4],
[0, 0, 5, 2, 0, 6, 3, 0, 0]]
# if sucess print the grid
if(solve_sudoku(grid)):
print_grid(grid)
else:
print("No solution exists")
# The above code has been contributed by Harshit Sidhwa.
Output
3 1 6 5 7 8 4 9 2
5 2 9 1 3 4 7 6 8
4 8 7 6 2 9 5 3 1
2 6 3 4 1 5 9 8 7
9 7 4 8 6 3 1 2 5
8 5 1 7 9 2 6 4 3
1 3 8 9 4 7 2 5 6
6 9 2 3 5 1 8 7 4
7 4 5 2 8 6 3 1 9