更新那时间: 22:13 03-02-2020 逻辑存在问题:插入节点后,调整数的结构不正确。 待修复
------ 欢迎指正-------
1、参考资料:
书籍:《算法导论》
博文:http://www.cnblogs.com/fivestudy/fivestudy/p/10340647.html 原理讲的很棒。有动画,方便理解。
这个网站可以清晰看清楚平衡二叉树的插入删除等详细过程: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
源码:
#includeusing namespace std; struct node { int data; int height; node *lc; node *rc; node() : data(0) , height(0) , lc(0) , rc(0) { } }; // 平衡二叉树 class avltree2 { public: // 构造函数 avltree2() : root(NULL) { } virtual ~avltree2(){} //--------------------------------------------------------- // 返回结点的高度 int height(node *pnode) { return pnode == NULL ? 0 : pnode->height; } // 计算两个的最大值 int max(int a, int b) { return a > b ? a : b; } //------------------------------------------------------------ /* 旋转代码: LL型 RR型 LR型 RL型 */ // 左旋转, 函数命名方式是以二叉树插入结点的形状命名的,这里的左旋, // 对应的形状是 RR型,即在结点右孩子插入结点。 node *rotate_rr(node *pnode) { node *ret_node = NULL; if (NULL != pnode) { // 保存失衡结点的右孩子 node *loss_balance_node_rc = pnode->rc; // 将失衡结点的右孩子的左孩子赋值给失衡结点的右孩子 pnode->rc = loss_balance_node_rc->lc; // 将失衡结点作为失衡结点的左孩子 loss_balance_node_rc->lc = pnode; // 更新失衡结点与新根结点的高度 pnode->height = max(height(pnode->lc), height(pnode->rc)) + 1; loss_balance_node_rc->height = max( height( loss_balance_node_rc->lc), height(loss_balance_node_rc->rc)) + 1; ret_node = loss_balance_node_rc; } return ret_node; } // 右旋, 函数名是以插入结点后的形式命名的,这里是 // 将新结点插入后,形成LL形状, node *rotate_ll(node *pnode) { node *ret_node = NULL; if (NULL != pnode) { node *loss_balance_node_lc = pnode->lc; if (NULL != loss_balance_node_lc) { // 将失衡结点的左孩子的右孩子为失衡结点的左孩子 pnode->lc = loss_balance_node_lc->rc; // 将失衡结点作为失衡结点左孩子的右孩子 loss_balance_node_lc->rc = pnode; // 更新高度 pnode->height = max(height(pnode->lc), height(pnode->rc)) + 1; loss_balance_node_lc->height = max( height(loss_balance_node_lc->lc), height(loss_balance_node_lc->rc)) + 1; } ret_node = loss_balance_node_lc; } return ret_node; } // LR 型 // 函数命名方式同上, 需要先左旋在右旋 node* rotate_lr(node *pnode) { if (NULL != pnode) { pnode->lc = rotate_rr(pnode->lc); pnode = rotate_ll(pnode); } return pnode; } // RL型 // 同上,需要先右旋,再左旋 node *rotate_rl(node *pnode) { if (NULL != pnode) { // 先右旋再左旋 pnode->rc = rotate_ll(pnode->rc); pnode = rotate_rr(pnode); } return pnode; } //------------------------------------------------------------ // 计算pnode结点的平衡因子 int get_balance_factor(node *pnode) { // 平衡因子= 左孩子 - 右孩子 return (NULL == pnode) ? 0 : height(pnode->lc) - height(pnode->rc); } // 找到以pnode为根结点的最小结点 node *get_min(node *pnode) { if (NULL == pnode) return pnode; while (pnode->lc) pnode = pnode->lc; return pnode; } // 找到以pnode为根结点的最大结点 node *get_max(node *pnode) { if (NULL == pnode) { return pnode; } while (pnode->rc) pnode = pnode->rc; return pnode; } // 插入结点 void insert(int key) { root = insert(root, key); } // 删除结点值为key的结点 void remove_node(int key) { if (NULL == root) return; // del_node(root, key); root = del_node2(root, key); } // 中序遍历 void in_order_traverse() { if (NULL == root) return; in_order(root); } // 删除整棵树 void remove() { if (NULL == root) return; remove(root); } // 前序遍历 void pre_order_traverse() { if (NULL == root) return; pre_order(root); } private: // 删除所有结点 void remove(node *pnode) { if (pnode) { remove(pnode->lc); remove(pnode->rc); delete pnode; } pnode = NULL; } // 前序遍历 void pre_order(node *pnode) { if (NULL != pnode) { cout << pnode->data << ", height = " << pnode->height << " "; pre_order(pnode->lc); pre_order(pnode->rc); } } // 中序遍历 void in_order(node *pnode) { if (NULL != pnode) { in_order(pnode->lc); cout << pnode->data << ", height = " << pnode->height << " "; in_order(pnode->rc); } } // 插入 node* insert(node *pnode, int key) { // 为空,则创建结点 if (NULL == pnode) { pnode = new(std::nothrow) node; if (NULL != pnode) { pnode->data = key; pnode->height = 1; return pnode; } } // 1、插入值比当前结点的值还要小,应该继续找左子树 if (key < pnode->data) { pnode->lc = insert(pnode->lc, key); } // 2、比当前值大。应该继续找当前结点的右子树 else if (key > pnode->data) { pnode->rc = insert(pnode->rc, key); } else { // 3、相等,树中已经存在插入的结点了,无法继续插入相同结点 return pnode; } // 4、更新结点的高度 pnode->height = max(height(pnode->lc), height(pnode->rc)) + 1; // 5、获取插入后的平衡情况的平衡因子 int pnode_bf = get_balance_factor(pnode); // 6、下面开始判断新插入节点的平衡因子,当前插入结果是否需要旋转结点 // 6.1 若为LL型,右旋 if ( (1 < pnode_bf) && (key < pnode->data) ) return rotate_ll(pnode); // 6.2 若为RR型,左旋 if ( (-1 > pnode_bf) && (key > pnode->data) ) return rotate_rr(pnode); // 6.3 若为LR型 if ( (1 < pnode_bf) && (key > pnode->data) ) return rotate_lr(pnode); // 6.4 若为RL型 if ( (-1 > pnode_bf) && (key < pnode->data) ) return rotate_rl(pnode); return pnode; } // 找到参数结点的父节点 node *get_parent_node(node *pnode) { if (NULL == pnode) { return pnode; } node *parent_node = NULL; int key = pnode->data; node *cur_node = root; while (cur_node) { if (key == cur_node->data) break; else if (key < cur_node->data) { parent_node = cur_node; cur_node = cur_node->lc; } else if (key > cur_node->data) { parent_node = cur_node; cur_node = cur_node->rc; } } return parent_node; } // 删除 node *del_node2(node *pnode, int key) { if (NULL == pnode) { return pnode; } // 找 删除结点的位置 if (key < pnode->data) { pnode->lc = del_node2(pnode->lc, key); } else if (key > pnode->data) { pnode->rc = del_node2(pnode->rc, key); } else { // 找到删除结点, // 3.1 若删除结点同时存在左右孩子 if ( (NULL != pnode->lc) && (NULL != pnode->rc) ) { // 需要从左右子树中最高的那棵树开始删除 // 从左子树中开始删除 if (height(pnode->lc) > height(pnode->rc)) { // 找到左子树中最大的结点,替换当前结点 node *pre_node = get_max(pnode->lc); // 将当前结点的值替换为前驱结点的值 pnode->data = pre_node->data; // 删除左子树中最大的结点 pnode->lc = del_node2(pnode->lc, pnode->data); } // 删除的结点从右子树中开始找 else { // 找到后继结点 node *successor_node = get_min(pnode->rc); // 将删除结点的值赋值给当前结点 pnode->data = successor_node->data; // 删除后继结点中指定结点的值 pnode->rc = del_node2(pnode->rc, pnode->data); } } // 3.2 若只有左孩子 else if ((NULL != pnode->lc) && (NULL == pnode->rc) ) { // 指向需要删除的结点 node *del_node_tmp = pnode->lc; // 将孩子的值赋值给删除结点 pnode->data = del_node_tmp->data; // 将父节点指向孩子结点的分支设置为NULL pnode->lc = NULL; delete del_node_tmp; del_node_tmp = NULL; } // 3.3 若只有右孩子 else if ( (NULL == pnode->lc) && (NULL != pnode->rc)) { // 指向需要删除的结点 node *del_node_tmp = pnode->rc; pnode->data = del_node_tmp->data; // 将分支设置为NULL del_node_tmp->rc = NULL; delete del_node_tmp; del_node_tmp = NULL; } // 3.4 删除的是叶子结点 else { node *pnode_pa = get_parent_node(pnode); if (NULL != pnode_pa) { if (pnode == pnode_pa->lc) pnode_pa->lc = NULL; else if (pnode == pnode_pa->rc) pnode_pa->rc = NULL; } // 说明只有根结点 else root = NULL; delete pnode; pnode = NULL; } } // 为了保证树的平衡 if (NULL == pnode) return pnode; // ------- 删除节点后,需要做平衡 pnode->height = max(height(pnode->lc), height(pnode->rc)) + 1; // 当前结点的平衡因子 int pnode_bf = get_balance_factor(pnode); // LL型 if ( (1 < pnode_bf) && (0 <= get_balance_factor(pnode->lc)) ) { return rotate_ll(pnode); } // LR型 if ( (1 < pnode_bf) && (0 > get_balance_factor(pnode->lc)) ) { return rotate_lr(pnode); } // RR型 if ( (-1 > pnode_bf) && (0 >= get_balance_factor(pnode->rc)) ) { return rotate_rr(pnode); } // RL型 if ( (-1 > pnode_bf) && (0 < get_balance_factor(pnode->rc)) ) { return rotate_rl(pnode); } return pnode; } private: node *root; }; int main() { avltree2 tree; int insert_key = 0; cout << "插入开始,结束插入 输入-1" << endl << endl << endl; while (1) { cout << "请输入插入值:"; cin >> insert_key; if (-1 == insert_key) break; tree.insert(insert_key); cout << endl << "插入后,中序遍历结果:"; tree.in_order_traverse(); cout << endl << endl; } cout << "前序遍历:"; tree.pre_order_traverse(); cout << endl; cout << "========================================" << endl; cout << "开始删除, 请输入删除元素的值, 结束输入-1" << endl << endl; int del_key = 0; while (1) { cout << "请输入删除结点值: "; cin >> del_key; if (-1 == del_key) break; tree.remove_node(del_key); cout << "删除后,中序遍历:"; tree.in_order_traverse(); cout << endl << "删除后,前序遍历:"; tree.pre_order_traverse(); cout << endl << endl; } cout << endl << endl << endl << "----------------------------" << endl << endl; cout << "删除树" << endl; tree.remove(); return 0; }
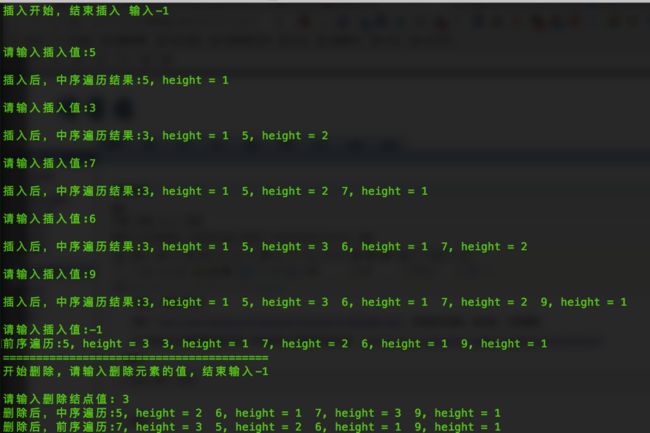
2、结果:
3、GitHub 地址:https://github.com/mohistH/base_data_structure