概要
上一篇文章有点偏重于技术的实施了,对选股的思路描述得有些含糊不清,所以在这里先复述一遍,然后再聊聊这次实验的思想。
上篇文章提到,如果要做一个投资组合,那么要尽量选取一些相关性特别低的股票以规避风险,正如乔尔-格林布拉特在《不够聪明也能成为股市天才》一书中特别指出的,持有8只股票会消除只拥有1只股票所承担的81%的风险,持有32只股票会消除96%的风险。不过其也得出结论认为:“买入不同行业中6只或8只股票之后,为减少风险再添加更多只股票到投资组合之中,其努力所得的益处很小。”
尚且不说收益的多少,主要的目的是为了降低风险,所以才通过机器学习的手段来计算各个股票之间的相关性,以选出一些差异大的股票作为投资目标。
ok,说完上篇文章,我们回到这里。
这篇文章讲的是另一种思路,找出走势最为平稳的股票,
通过ARIMA模型来预测股票走势。
当然,也并非所有的股票都可以进行预测,尤其是在中国市场,你懂得这里要预测找的是价格走势非常平稳的股票,如何判别其稳定性?首先要理解什么是均值回归。
均值回归是金融学中的一个重要规律,主要是指资产价格无论高于或低于价值中枢就会以较高的概率向中枢回归的趋势。虽然源于西方金融学理论,均值回归本质上与中国传统哲学中物极必反的道理是一致的。
战国时期《吕氏春秋.博志》中有“全则必缺,极则必反,盈则必亏”的阐述,意即事物发展到极端则会向相反方向转化,这说的其实就是均值回归的现象。
均值回归的现象最先是由芝加哥大学行为金融学教授理查德·塞勒与威斯康星大学沃纳·德邦特教授提出的。在1985年发表的《股市是否反应过度》一文中,塞勒和德邦特提出了他们的研究发现:以3至5年为周期,原本表现不佳的股票开始摆脱困境而走好,而原先的赢家股票则步入下坡路,这种反向走势不仅表现在股价上,而且表现在公司的盈利上。
对于公司和行业盈利的均值回归,迈克尔·波特的竞争理论给出了一个合理的解释:当行业盈利丰厚时新的进入者竞争拉低了盈利,当行业无利可图时退出者为行业盈利恢复创造了条件。
我想上面已经解释的很清楚了,所以很显然,本次实验的目的就是为了找出最具备均值回归性质的股票,并对其进行预测。
实验过程
为了节省网络爬虫时间,我们依然使用上次实验存储下来的数据:300份从2014年1月1日只2018年1月1日的股票历史交易数据。
for f in files:
symbol = f.split('.')[0]
try:
data = pd.read_csv(os.path.join(parent, f))
except:
pass
else:
if len(data) > 900:
symbols.append(symbol)
data.index = pd.to_datetime(data['date'])
select_dict[symbol] = data
以上,我创建了一个字典,其中包括股票的代码,以及对应的历史交易数据。先来随机选取一组数据,看看其长的样子
random_data = select_dict[np.random.choice(symbols)]
random_data.close.plot()
这里横坐标表示股票交易的时间,纵坐标为股票的价格。
聊点算法
对于时间序列的预测, 自回归积分滑动平均模型(Auto regressive Integrated Moving Average Model,简记ARIMA)是时间序列中最为重要的模型之一。 其中 AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。 所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
模型的建立大致分为以下一个步骤:
1. 获取被观测系统时间的序列数据;
2. 将数据绘图,观测是否为平稳的时间序列;对于非平稳的时间序列要先进行d阶差分运算,化为平稳时间序列;
3. 对平稳的时间序列分别求得其自相关稀疏ACF和偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层p和阶数q;
4. 由以上得到的d、p、q,得到ARIMA模型,然后开始对得到的模型进行检验。
平稳性检验
我们知道序列平稳性是进行时间序列分析的前提条件,很多人都会有疑问,为什么要满足平稳性的要求呢?
在大数定理和中心定理中要求样本同分布(这里同分布等价于时间序列中的平稳性),而我们的建模过程中有很多都是建立在大数定理和中心极限定理的前提条件下的,如果它不满足,得到的许多结论都是不可靠的。对于平稳性检验,可以使用观察法和单位根检验(Unit Root test)
这里可以再延伸聊一聊Unit Root test。
什么是单位根检验? 单位根检验是针对宏观经济数据序列、货币金融数据序列中是否具有某种统计特性而提出的一种平稳性检验的特殊方法,单位根检验的方法有很多种,包括ADF检验、PP检验、NP检验等。 单位根检验是建立ARMA模型、ARIMA模型、变量间的协整分析、因果关系检验等的基础。
自Nelson和Plosser利用ADF检验研究了美国名义GNP等14个历史经济和金融时间序列的平稳性以后,单位根检验业已成为分析经济和金融时间序列变化规律和预测的重要组成部分。
接下来我们就用ADF test方法来进行单位根检验。
我们先用上面这只股票来进行ADF test
close = random_data.close
adf_result = adfuller(close, 1)
print('adf value: {}'.format(adf_result[0]))
print('p value: {}'.format(adf_result[1]))
print('1%: {}'.format(adf_result[4]['1%']))
print('5%: {}'.format(adf_result[4]['5%']))
print('10%: {}'.format(adf_result[4]['10%']))
运行结果如下:
adf value: -2.072270548181211
p value: 0.25580991476184356
1%: -3.4372303791313144
5%: -2.864577551835195
10%: -2.568387363624452
要理解这个结果,可以试着看看帮助文档
Returns
-------
adf : float
Test statistic
pvalue : float
MacKinnon's approximate p-value based on MacKinnon (1994, 2010)
usedlag : int
Number of lags used
nobs : int
Number of observations used for the ADF regression and calculation of
the critical values
critical values : dict
Critical values for the test statistic at the 1 %, 5 %, and 10 %
levels. Based on MacKinnon (2010)
icbest : float
The maximized information criterion if autolag is not None.
resstore : ResultStore, optional
A dummy class with results attached as attributes
P值是t统计量对应的概率值,所以t和p两者是等效的。P值要求小于给定的显著性水平,一般是0.05、0.01等,p越接近于0越好。
其次,我们再来看看各水平值的设定意义。
1%:严格拒绝原假设;
5%:拒绝原假设,
10%: 类推。
ADF检验的原假设是存在单位根,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。
注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设 。
由此见得,这份股票的数据从结果上来看并不稳定,有很多随机游走值,故此不建议建立模型。
为了选出一份表现平稳的数据,我们可以把所有的数据都进行ADF test,找出最平稳的一份数据。
import operator
adf_dict = {}
for s in symbols:
data = select_dict[s]
p_value = adfuller(data['close'], 1)[1]
adf_dict[s] = p_value
sorted_adf = sorted(adf_dict.items(), key=operator.itemgetter(1))
我们看一下排列靠前的结果
('002118', 0.006636571374405614),
('002391', 0.012480193802360722),
('002585', 0.013050042497239251),
('000848', 0.014014607139028454),
('000554', 0.014604189557314053),
('600078', 0.015523468245091676),
('002565', 0.01585143054445688),
('002459', 0.016432616096700544),
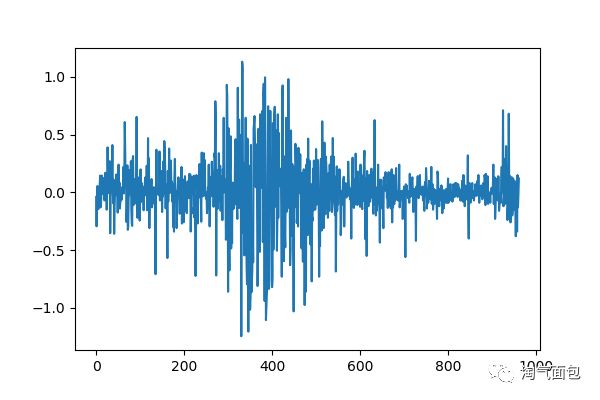
ok,002118 这小伙的表现最为稳定。可以看下其股票每天的价差走势到底呈现什么样
diff_002118 = np.diff(select_dict['002118'].close, n=1)
plt.plot(diff_002118)
plt.show()
结论
至此,本文的知识点就已经讲完了。那么如何利用本次实验的结论来进行投资呢?
在我看来,其实可以和第一篇文章结合一下。我们完全可以通过技术手段在上千只股票中找出走势最为平稳的股票,在历史低点买进,历史高点卖出,因为其稳定的走势,也就增大了其盈利的概率。
其次,你不可能排除有喜欢抽风的公司,为了规避某只股票的风险,你可以对股市中所有的股票分析他们之间的相关性,买入不同种类的股票,以达到消除风险的目的。这种投资策略要比瞎买、听小道消息或者别人介绍靠谱的多。
题外话
其实刚开始此篇的文章的中心并非是寻找高度具备mean reverting性质的股票,而是想再深究一步,通过ARIMA进行未来走势的预测。
我开了32个线程,跑了两个小时的数据,找出最优的参数,并且数据表现良好,但是在预测时,结果并不如意,所以那一部分的实验就不贴上来了,免得误导各位看官。不过想想也对,面对每天变幻莫测的股市,就算利用强化学习也未必能够准确预测出第二天的走势。
当然,重点并非在于算法,而是如何研究出可盈利的策略。这仅仅是开始,距离真正的algo trading还早着呢,我们继续!