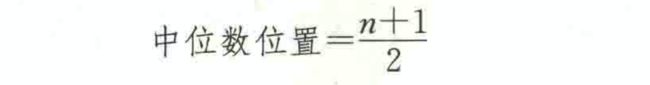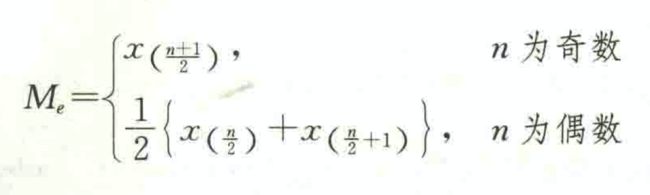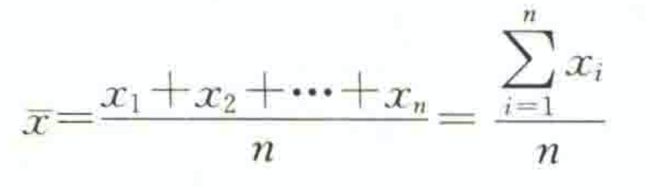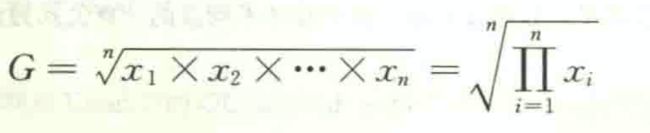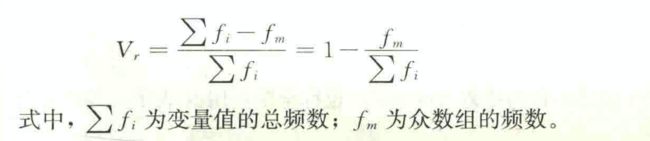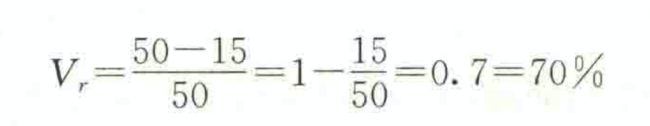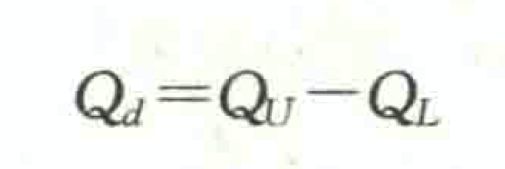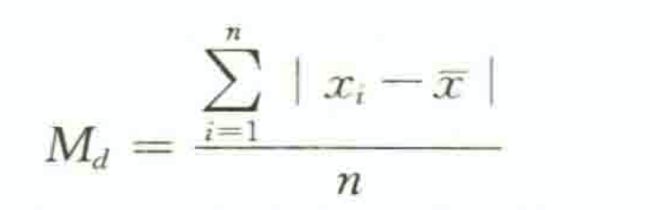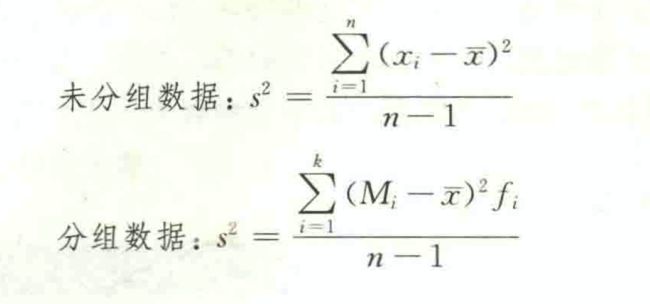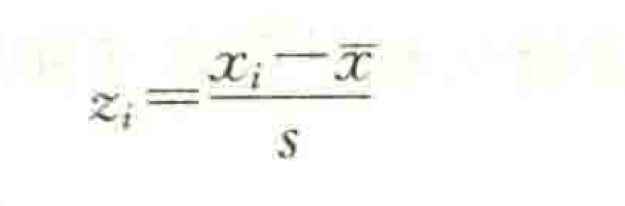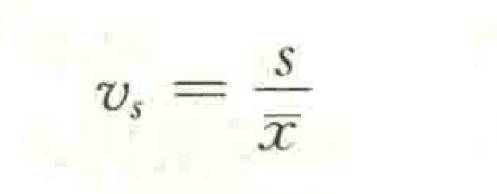数据分布的特征可以从三个方面进行测度和描述:
- 一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;
- 二是分布的离散程度,反映各数据远离其中心值的趋势;
- 三是分布的形状,反映数据分布的偏态和峰态。
集中趋势
集中趋势(central tendency)
是指一组数据向某一中心值靠拢的程度,它反映了一组数据中心点的位置所在。
众数(mode)
是一组数据中出现次数最多的变量值,用M0表示。众数主要用于测度分类数据的集中趋势,也可作为顺序数据以及数值型数据集中趋势的测度值。一般情况下,只有在数据量较大的情况下众数才有意义。
例题:
在某城市中随机抽取9个家庭,调查得到每个家庭的人均月收入数据如下(单位:元)。要求计算人均月收入的众数。
|1080|750|1080|1080|850|960|2000|1250|1630|
解:
人均月收入出现频数最多的是1080,因此,众数M0=1080元。
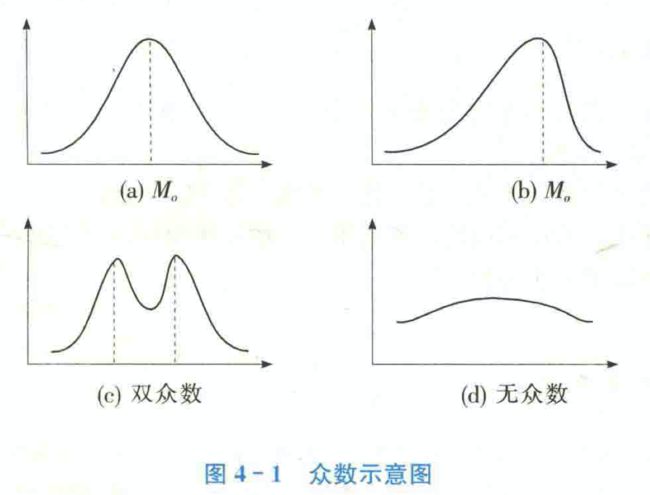
从分布的角度看,众数是具有明显集中趋势点的数值,一组数据分布的最高峰点所对应的数值即为众数。当然,如果数据的分布没有明显的集中趋势或最高峰点,众数可能不存在;如果有两个或多个最高峰点,则可以有两个或多个众数。
中位数(median)
中位数(median)是一组数据排序后处于中间位置上的变量值,用Me表示。
设一组数据为x1,x2,…,xn,按从小到大的顺序排序后为xa,x2)…,xn,则中位数为:
例题:
下面再看看当数据个数为偶数时怎样计算中位数。假定在例4.5中抽取了10个家庭, 每个家庭的人均月收入数据排序后为:
|660|750|780|850|960|1080|1250|1500|1630|2000|
四分位数(quartile)
也称四分位点,它是一组数据排序后处于25%和75%位置上的值四分位数通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。
设下四分位数为Q2.,上四分位数为Q,根据四分位数的定义有:
例题:
根据例4.5中9个家庭的收入调查数据,计算人均月收入的四分位数。
|660|750|780|850|960|1080|1250|1500|1630|2000|
平均数(mean)
简单平均数与加权平均数,平均数也称为均值(mean),它是一组数据相加后除以数据的个数得到的结果。
几何平均数(geometric mean)
一种特殊的平均数,几何平均数(geometric mean)是n个变量值乘积的n次方根,用G表示。计算公式为:
几何平均数主要用于计算平均比率。当所掌握的变量值本身是比率形式时,采用几何平均法计算平均比率更为合理。在实际应用中,几何平均数主要用于计算现象的平均增长率。
例题:
‘’‘
一位投资者持有一种股票,连续4年的收益率分别为4.5%,2.1%,25.5%,1.9%。要求计算该投资者在这4年内的平均收益率。
’‘’
众数、中位数和平均数的比较
1.众数、中位数和平均数的关系
从分布的角度看,众数始终是一组数据分布的最高峰值,中位数是处于一组数据中间位置上的值,而平均数则是全部数据的算术平均。因此,对于具有单峰分布的大多数数据而言,众数、中位数和平均数之间具有以下关系:
2.众数、中位数和平均数的持点与应用场合
众数是一组数据分布的峰值,不受极端值的影响。其缺点是具有不唯一性。众数只有在数据量较多时才有意义,当数据量较少时,不宜使用众数。众数适合作为分类数据的集中趋势测度值。
中位数是一组数据中间位置上的值,不受数据极端值的影响。当一组数据的分布偏斜程度较大时,使用中位数也许是一个好的选择。中位数适合作为顺序数据的集中趋势测度值。
平均数是针对数值型数据计算的,而且利用了全部数据信息,平均数的主要缺点是易受数据极端值的影响,对于偏态分布的数据,平均数的代表性较差。
离散程度
异众比率(varlation ratio)
是指非众数组的频数占总频数的比例,用Vr,表示。异众比率主要用于衡量众数对一组数据的代表程度。异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性越差;异众比率越小,说明非众数组的频数占总频数的比重越小,众数的代表性越好。
其计算公式为:
例题:
| 饮料类型 | 总计 |
|---|---|
| 果汁 | 6 |
| 矿泉水 | 10 |
| 绿茶 | 11 |
| 其他 | 8 |
| 碳酸饮料 | 15 |
这说明在所调查的50人当中,购买其他类型饮料的人数占70%,异众比率比较大。因此, 用“碳酸饮料”来代表消费者购买饮料类型的状况不是很好。
四分位差(quartile deviation)
也称为内距或四分间距(inter-quartile range),它是上四分位数与下四分位数之差,用Q表示。四分位差反映了中间50%的数据的离散程度,数值越小,说明中间的数据越集中;数值越大,说明中间的数据越分散。四分位差不受极值的影响。其计算公式为:
极差
一组数据的最大值与最小值之差称为极差(range),也称全距,用R表示。其计算公式为:
平均差(mean deviation)
也称平均绝对离差(mean absolute deviation),它是各变量值与其平均数离差绝对值的平均数,用Md表示。
根据未分组数据计算平均差的公式为:
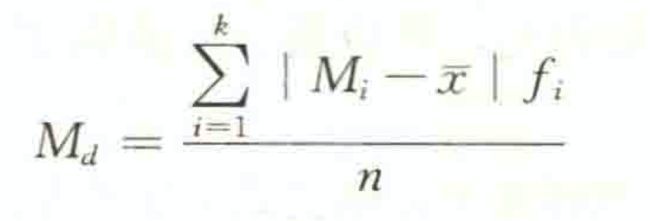
根据分组数据计算平均差的公式为:
其中Mi为组中值;fi为频数
方差和标准差
方差(或标准差)能较好地反映出数据的离散程度,是应用最广的离散程度的测度值。
方差
方差(varlance) 是各变量值与其平均数离差平方的平均数。它在数学处理上通过平方的办法消去离差的正负号,然后再进行平均。
标准差
方差的平方根称为 标准差(standard devi ation) 。
自由度
样本方差是用样本数据个数减1后去除离差平方和,其中样本数据个数减1即n-1 称为自由度(degree of freedom)。
相对位置的度量
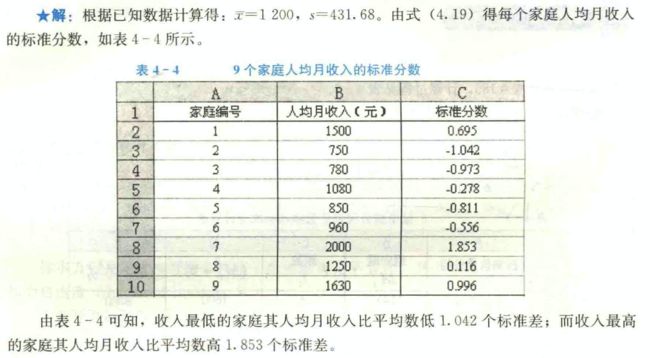
(1)标准分数。
变量值与其平均数的离差除以标准差后的值称为标准分数( standard score),也称标准化值或z分数。标准分数给出了一组数据中各数据的相对位置。比如,如果某个数据的标准分数为-1.5,就知道该数据比平均数低1.5个标准差。设标准分数为z,则有
标准分数具有平均数为0、标准差为1的特性。实际上,x分数只是将原始数据进行了线性变换,它并没有改变一个数据在该组数据中的位置,也没有改变该组数据分布的形状,而只是将该组数据变为平均数为0、标准差为1。
(2)经验法则
经验法则适合对称分布的数据,当一组数据对称分布时,经验法则表明:
约有68%的数据在平均数士1个标准差的范围之内。
约有95%的数据在平均数士2个标准差的范围之内。
约有99%的数据在平均数士3个标准差的范围之内。
(3)切比雪夫不等式
如果一组数据不是对称分布,这时可使用切比雪夫不等式(Chebyshev' s inequality),它对任何分布形态的数据都适用切比雪夫不等式提供的是“所占比例至少是多少”,对于任意分布形态的数据,根据切比雪夫不等式,至少有(1-1/k2)的数据落在土k个标准差之内。其中k是大于1的任意值,但不一定是整数。对于k=2,3,4,该不等式的含义是:
至少有75%的数据在平均数士2个标准差的范围之内。
至少有89%的数据在平均数士3个标准差的范围之内。
至少有94%的数据在平均数士4个标准差的范围之内。
离散系数
离散系数(coefficient of variation)也称为变异系数,它是一组数据的标准差与其相应的平均数之比。离散系数是测度数据离散程度的统计量,主要用于比较不同样本数据的离散程度。离散系数大,说明数据的离散程度也大;离散系数小,说明数据的离散程度也小。其计算公式为:
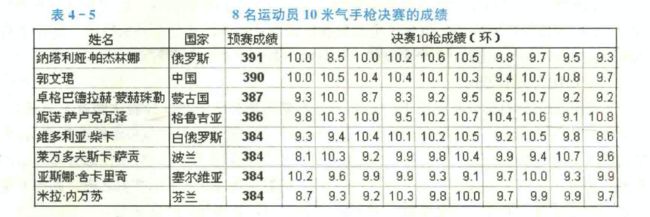
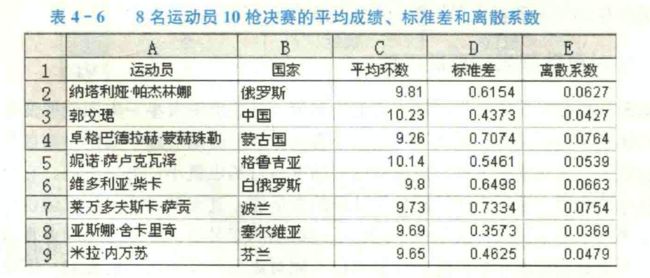
例:
从离散系数可以看出,在最后10枪的决赛中,发挥比较稳定的运动员是塞尔维亚的亚斯娜・舍卡里奇和中国的郭文珺,发挥不稳定的运动员是蒙古国的卓格巴德拉赫・蒙赫珠勒和波兰的菜万多夫斯卡・萨贡。
分布的形状
偏态(skewness)
是对数据分布对称性的测度。测度偏态的统计量是偏态系数(coefficient of skewness), 记作SK。偏态系数的计算方法有很多。
在根据未分组的原始数据计算偏态系数时,通常采用下面的公式:
根据分组数据计算偏态系数,可采用下面的公式:
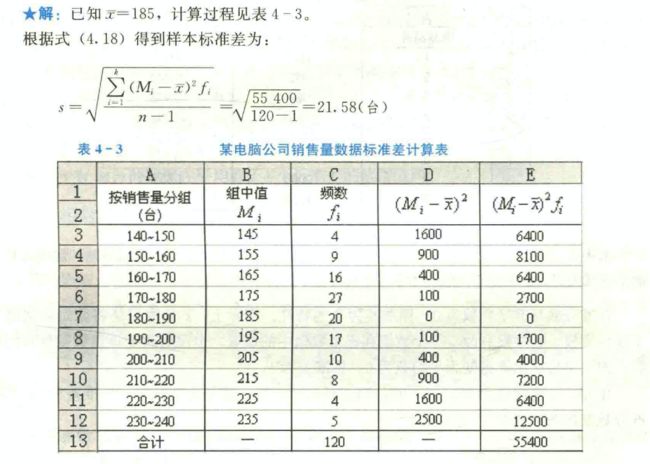
例:
偏态系数为正值,但数值不是很大,说明电脑销售量的分布为右偏分布,但偏斜程度不是很大。从第3章的图3-16销售量分布的直方图中也可以看出这一点。
“峰态”(kurtosis)
是对数据分布平峰或尖峰程度的测度。测度峰态的统计量是峰态系数(coefficient of kurtosis),记作K。峰态通常是与标准正态分布相比较而言的。如果一组数据服从标准正态分布,则峰态系数的值等于0;若峰态系数的值明显不等于0,则表明分布比正态分布更平或更尖,通常称为平峰分布或尖峰分布。
总结
数据概念
| 名称 | LaTex | 简写 |
|---|---|---|
| 众数 | M_o |
image.png
|
| 中位数 | M_e |
image.png
|
| 上四分卫数 | Q_U |
image.png
|
| 下四分卫数 | Q_L |
image.png
|
| 平均数 | \overline{x} |
image.png
|
| 几何平均数 | \overline{G} |
image.png
|
| 异众比率 | V_r |
image.png
|
| 四分位差 | Q_d |
image.png
|
| 极差 | R | R |
| 平均差 | M_d |
image.png
|
| 方差 | s^2 |
image.png
|
| 标准差 | s | s |
| 标准分数 | z | z |
| 离散系数 | v_s |
image.png
|
| 偏态系数 | SK | SK |
| 峰态系数 | K | K |
Excel操作
利用 Excel中的 MODE函数可以计算一组数值型数据的众数。
利用 Excel中的 MEDIAN函数可以计算一组数值型数据的中位数。
利用 Excel中的 QUARTILE函数可以计算一组数值型数据的四分位数。
利用 Excel中的 AVERAGE函数可以计算一组数值型数据的算数平均数。
利用 Excel中的 GEOMEAN函数可以计算一组数值型数据的几何平均数。
利用 Excel中的 AVEDEV函数可以计算一组数值型数据的平均差。
利用 Excll中的 STDEV函数可以计算一组数值型数据的样本标准差。
利用 Excel中的 SKEW函数可以计算一组数值型数据的偏态系数。
本章我们介绍了数据分布特征的各种测度值,其中多数可以通过 Excel【数据分析】工具中的【描述统计】命令得出计算结果。