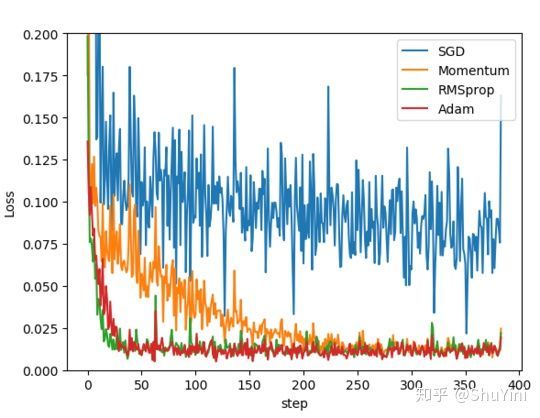
本文是从网上的资料加上自己的总结而来的,要感谢
PyTorch 学习笔记(七):PyTorch的十个优化器: https://blog.csdn.net/u011995719/article/details/88988420
Pytorch中常用的四种优化器SGD、Momentum、RMSProp、Adam:https://zhuanlan.zhihu.com/p/78622301
机器学习:各种优化器Optimizer的总结与比较:https://blog.csdn.net/weixin_40170902/article/details/80092628
PyTorch中文文档:https://pytorch-cn.readthedocs.io/zh/latest/
PyTorch英文文档:https://pytorch.org/docs/stable/index.html
从最新(1.2.0)版本的Pytorch文档中可以知道,pytorch一共有11个优化器(当然,可实现的算法不止11种),分别是
SGD
ASGD
Adagrad
Adadelta
Rprop
RMSprop
Adam
Adamax
SparseAdam
AdamW
L-BFGS
下面分析加粗的常用优化器:
1、SGD (实现随机梯度下降算法(momentum、nesterov可选))
torch.optim.SGD(params,lr=
参数:
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float) – 学习率
--momentum (float, 可选) – 动量因子(默认:0,通常设置为0.9,0.8)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认:0)
--dampening (float, 可选) – 动量的抑制因子(默认:0)
--nesterov (bool, 可选) – 使用Nesterov动量(默认:False)论文:http://www.cs.toronto.edu/~hinton/absps/momentum.pdf
例子:
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()
优点:①使用mini-batch的时候,可以收敛得很快
缺点:①在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确
②不能解决局部最优解的问题
推荐程度:不推荐!
1.1、使用动量(Momentum)的随机梯度下降法(SGD)
更新的时候在一定程度上保留之前更新的方向,用法为在torch.optim.SGD的momentum参数不为零,
优点:加快收敛速度,有一定摆脱局部最优的能力,一定程度上缓解了没有动量的时候的问题
缺点:仍然继承了一部分SGD的缺点
推荐程度:可以一试
1.2、使用牛顿加速度(NAG, Nesterov accelerated gradient)的随机梯度下降法(SGD)
可以理解为往标准动量中添加了一个校正因子
理解策略:在Momentun中小球会盲目地跟从下坡的梯度,容易发生错误。所以需要一个更聪明的小球,能提前知道它要去哪里,还要知道走到坡底的时候速度慢下来而不是又冲上另一个坡
优点:梯度下降方向更加准确
缺点:对收敛率的作用却不是很大
推荐程度:不如不试
2、ASGD(随机平均梯度下降(Averaged Stochastic Gradient Descent))
简单地说ASGD就是用空间换时间的一种SGD,详细可参看论文:http://riejohnson.com/rie/stograd_nips.pdf
torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
参数:
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:1e-2)
--lambd (float, 可选) – 衰减项(默认:1e-4)
--alpha (float, 可选) – eta更新的指数(默认:0.75)
--t0 (float, 可选) – 指明在哪一次开始平均化(默认:1e6)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
推荐程度:很少见
3、AdaGrad算法
独立地适应所有模型参数的学习率,梯度越大,学习率越小;梯度越小,学习率越大
Adagrad适用于数据稀疏或者分布不平衡的数据集
论文:http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf
class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
参数:
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认: 1e-2)
--lr_decay (float, 可选) – 学习率衰减(默认: 0)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
优点:它可以自动调节学习率,不需要人为调节
缺点:仍依赖于人工设置一个全局学习率,随着迭代次数增多,学习率会越来越小,最终会趋近于0
推荐程度:不推荐
4、AdaDelta算法
是Adagard的改进版,对学习率进行自适应约束,但是进行了计算上的简化,加速效果不错,训练速度快
论文:https://arxiv.org/pdf/1212.5701.pdf
torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
参数:
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--rho (float, 可选) – 用于计算平方梯度的运行平均值的系数(默认:0.9)
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-6)
--lr (float, 可选) – 在delta被应用到参数更新之前对它缩放的系数(默认:1.0)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
优点:避免在训练后期,学习率过小;初期和中期,加速效果不错,训练速度快
缺点:还是需要自己手动指定初始学习率,初始梯度很大的话,会导致整个训练过程的学习率一直很小,在模型训练的后期,模型会反复地在局部最小值附近抖动,从而导致学习时间变长
在论文中提到AdaDelta有两个改进方法:
Accumulate Over Window
Correct Units with Hessian Approximation
推荐程度:可以试一试更好的
5、Rprop(弹性反向传播)
1、首先为各权重变化赋一个初始值,设定权重变化加速因子与减速因子。
2、在网络前馈迭代中当连续误差梯度符号不变时,采用加速策略,加快训练速度;当连续误差梯度符号变化时,采用减速策略,以期稳定收敛。
3、网络结合当前误差梯度符号与变化步长实现BP,同时,为了避免网络学习发生振荡或下溢,算法要求设定权重变化的上下限。
torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
参数
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:1e-2)
--etas (Tuple[float,float], 可选) – 一对(etaminus,etaplis), 它们分别是乘法的增加和减小的因子(默认:0.5,1.2)
--step_sizes (Tuple[float,float], 可选) – 允许的一对最小和最大的步长(默认:1e-6,50)
缺点:优化方法适用于full-batch,不适用于mini-batch,因此基本上没什么用
推荐程度:不推荐!不能用在mini-batch,想不到在什么时候能用
6、RMSProp(Root Mean Square Prop,均方根传递)
RProp的改进版,也是Adagard的改进版
思想:梯度震动较大的项,在下降时,减小其下降速度;对于震动幅度小的项,在下降时,加速其下降速度
RMSprop采用均方根作为分母,可缓解Adagrad学习率下降较快的问题
论文:https://arxiv.org/pdf/1308.0850v5.pdf http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
对于RNN有很好的效果
torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
参数
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:1e-2)
--momentum (float, 可选) – 动量因子(默认:0)
--alpha (float, 可选) – 平滑常数(默认:0.99)
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
--centered (bool, 可选) – 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
优点:可缓解Adagrad学习率下降较快的问题,并且引入均方根,可以减少摆动,适合处理非平稳目标,对于RNN效果很好
缺点:依然依赖于全局学习率
推荐程度:推荐!RMSProp算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一
7、Adam(AMSGrad)
将Momentum算法和RMSProp算法结合起来使用的一种算法,既用动量来累积梯度,又使得收敛速度更快同时使得波动的幅度更小,并进行了偏差修正
论文:https://arxiv.org/pdf/1412.6980.pdf
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
参数
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:1e-3)
--betas (Tuple[float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999)
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
优点:
1、对目标函数没有平稳要求,即loss function可以随着时间变化
2、参数的更新不受梯度的伸缩变换影响
3、更新步长和梯度大小无关,只和alpha、beta_1、beta_2有关系。并且由它们决定步长的理论上限
4、更新的步长能够被限制在大致的范围内(初始学习率)
5、能较好的处理噪音样本,能天然地实现步长退火过程(自动调整学习率)
6、很适合应用于大规模的数据及参数的场景、不稳定目标函数、梯度稀疏或梯度存在很大噪声的问题
推荐程度:非常推荐,基本上是最最常用的优化方法
8、Adamax
Adam的改进版,对Adam增加了一个学习率上限的概念,是Adam的一种基于无穷范数的变种
论文:https://arxiv.org/pdf/1412.6980.pdf
torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
参数:
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:2e-3)
--betas (Tuple[float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
优点:对学习率的上限提供了一个更简单的范围
推荐程度:非常推荐!其实也就是Adam的一个变种,差不了多少
9、Nadam
Adam的改进版,类似于带有Nesterov动量项的Adam,Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
这里先挖个坑,因为根据pytorch稳定版的文档好像还没封装Nadam函数,可是隔壁tensorflow已经有了,希望可以快点出来吧
10、SparseAdam
针对稀疏张量的一种“阉割版”Adam优化方法
torch.optim.SparseAdam(params,lr=0.001,betas=(0.9,0.999),eps=1e-08)
参数
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:2e-3)
--betas (Tuple[float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999)
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
优点:相当于Adam的稀疏张量专用版本
推荐程度:推荐,在处理稀疏张量的时候尤其推荐
11、AdamW
Adam的进化版,是目前训练神经网络最快的方式
论文:https://arxiv.org/pdf/1711.05101.pdf
torch.optim.AdamW(params,lr=0.001,betas=(0.9,0.999),eps=1e-08,weight_decay=0.01,amsgrad=False)
参数
--params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
--lr (float, 可选) – 学习率(默认:1e-3)
--betas (Tuple[float,float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999)
--eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
--weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 1e-2)
--amsgrad(boolean, optional) – 是否使用从论文On the Convergence of Adam and Beyond中提到的算法的AMSGrad变体(默认:False)
优点:比Adam收敛得更快
缺点:只有fastai使用,缺乏广泛的框架,而且也具有很大的争议性
推荐程度:观望!希望之后能成为主流
12、L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)
是一种在牛顿法基础上提出的一种求解函数根的算法,简单来说,L-BFGS和梯度下降、SGD干的同样的事情,但大多数情况下收敛速度更快
L-BFGS是对BFGS的改进,特点就是节省内存
是解无约束非线性规划问题最常用的方法
torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100,line_search_fn=None)
警告
这个optimizer不支持为每个参数单独设置选项以及不支持参数组(只能有一个)
目前所有的参数不得不都在同一设备上。在将来这会得到改进。
注意
这是一个内存高度密集的optimizer(它要求额外的param_bytes * (history_size + 1)个字节)。内存不符合要求,尝试减小history size,或者使用不同的算法。
参数
--lr (float) – 学习率(默认:1)
--max_iter (int) – 每一步优化的最大迭代次数(默认:20))
--max_eval (int) – 每一步优化的最大函数评价次数(默认:max * 1.25)
--tolerance_grad (float) – 一阶最优的终止容忍度(默认:1e-5)
--tolerance_change (float) – 在函数值/参数变化量上的终止容忍度(默认:1e-9)
--history_size (int) – 更新历史的大小(默认:100)
优点:收敛速度快、内存开销少,是解无约束非线性规划问题最常用的方法
缺点:使用条件严苛
推荐程度:酌情选择,根据自己的需要考虑是否真的需要使用这个算法
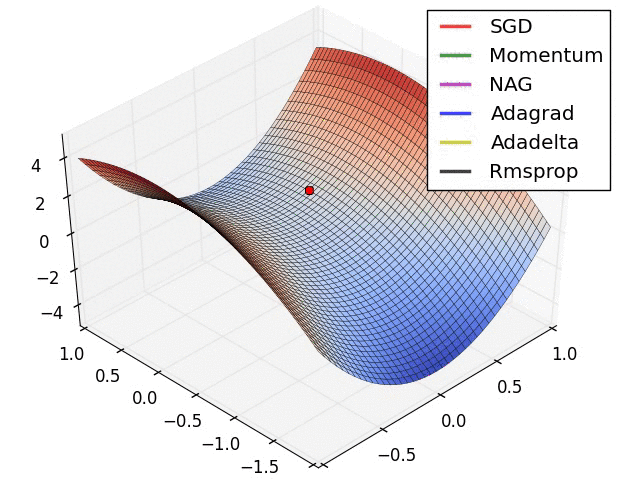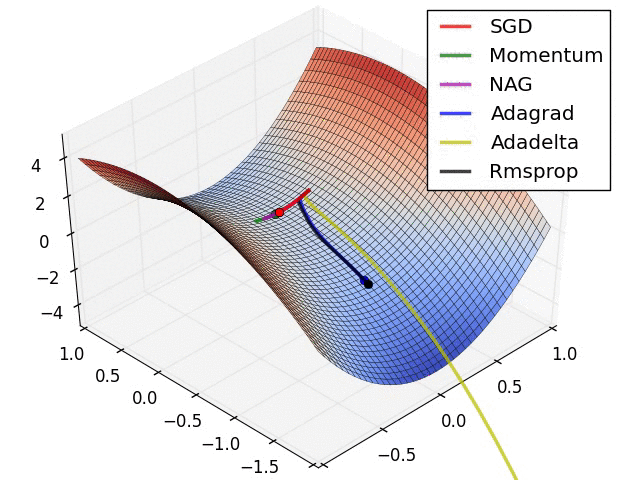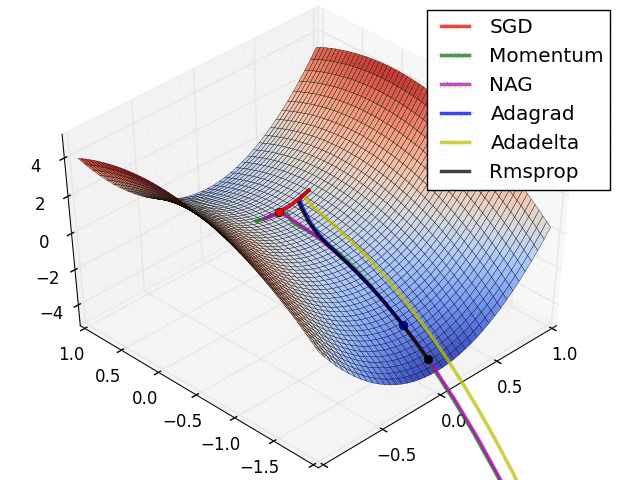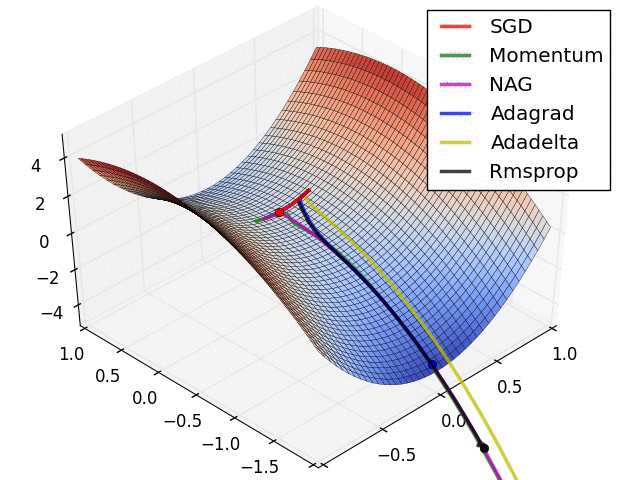
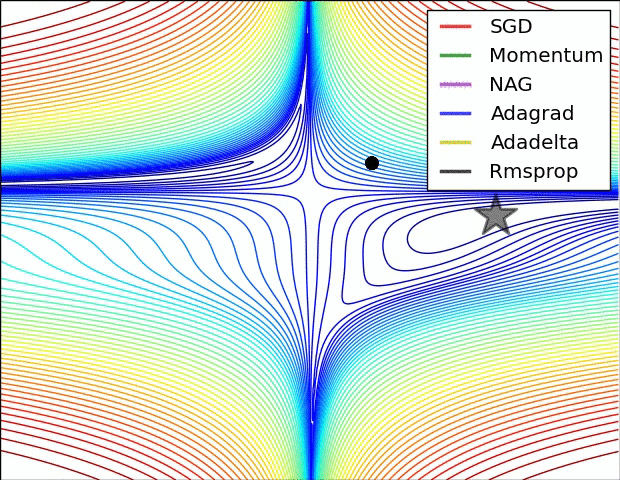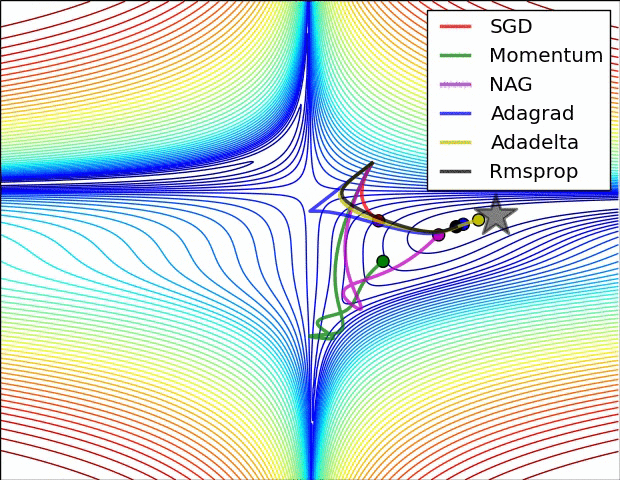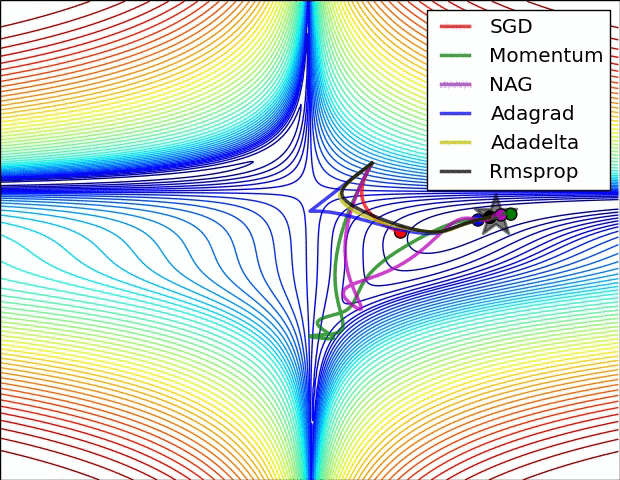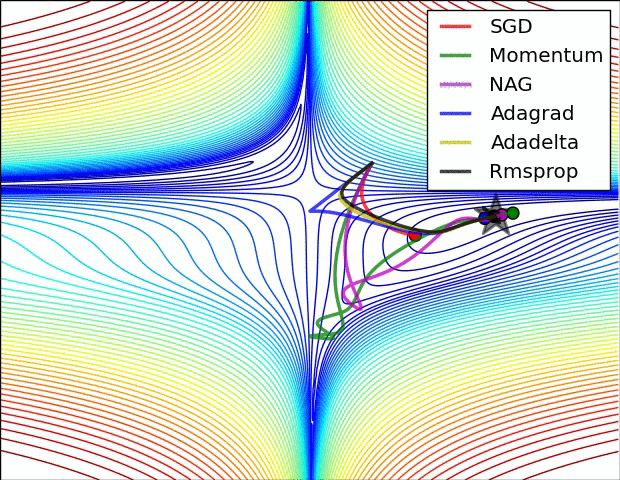
下面是一些算法的对比gif,都是摘自网上的: