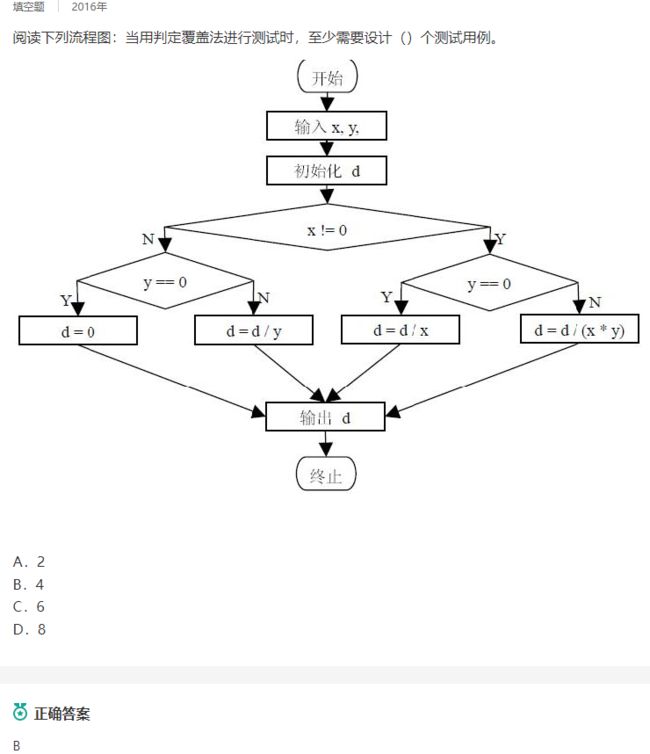
语句覆盖:所有的“语句”都要覆盖一遍
判定覆盖:包含语句覆盖,每个判断T、F各一次
条件覆盖:包含语句覆盖,每个条件T、F各一次,但不保证判定覆盖
判定条件覆盖:包含判定覆盖、条件覆盖
条件组合覆盖:每个条件的每种组合
路径覆盖:所有执行路径
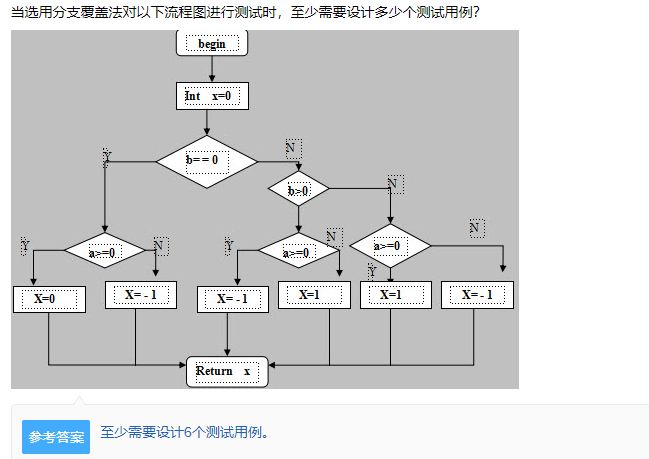
判定覆盖(也叫分支覆盖)
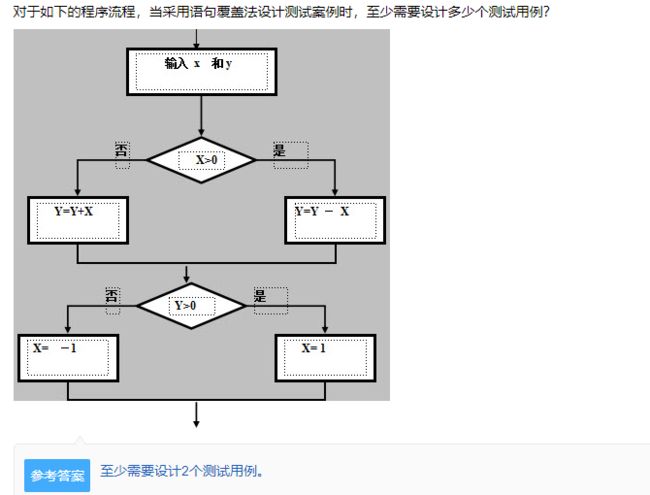
语句覆盖
References
http://people.cs.aau.dk/~bnielsen/TOV07/lektioner/whitebox-07.pdf
http://blog.sina.com.cn/s/blog_a4e88c4f0102vtdm.html
https://blog.csdn.net/LOVEYSUXIN/article/details/82592588
https://blog.csdn.net/cyjs1988/article/details/80341415
https://www.guru99.com/code-coverage.html
https://sites.google.com/site/swtestingconcepts/home/test-design-techniques/for-white-box/statement-branch-and-path-coverage
计算机硬件
某计算机指令长度为32位,有3种指令:双操作数指令、单操作数指令、无操作数指令。今采用扩展操作码的方式来设计指令,假设操作数地址为12位,己知有双操作数指令K条,单操作数指令L条,问无操作数指令有多少条?
答案:
解:对于双操作数指令,操作码长度为(32-12×2)=8位;
对于单操作数指令,操作码长度为(32-12)=20位,可扩展位为20-8=12位(在双操作数8位的基础上进行扩展,所以要减去8);
对于无操作数指令,操作码长度为32位,可扩展位为32-20=12位。
由于双操作数指令有K条,而双操作数最多有28条,所以留有(28-K)个编码用于扩展到单操作数指令;
单操作数指令有L条,而单操作数指令最多有(28-K)×212条,所以留有[(28-K)×212-L]个编码用于扩展到无操作数指令;
根据以上分析:无操作数指令条数=[(28-K)×212-L] ×212。
数据库
超键(super key):在关系中能唯一标识元组的属性集称为关系模式的超键
候选键(candidate key):不含有多余属性的超键称为候选键,也叫候选码,可以有多个候选码
主键(primary key):用户选作元组标识的一个候选键程序主键,也叫主码,只能有一个主码
外键(foreign key)如果关系模式R1中的某属性集不是R1的主键,而是另一个关系R2的主键则该属性集是关系模式R1的外键。
主属性 包含在任一候选关键字中的属性称主属性。候选码并集的属性
非主属性 不包含在主码中的属性称为非主属性。
结合实例的具体解释:
假设有如下两个表:
学生(学号,姓名,性别,身份证号,教师编号)
教师(教师编号,姓名,工资)
超键:
由超键的定义可知,学生表中含有学号或者身份证号的任意组合都为此表的超键。如:(学号)、(学号,姓名)、(身份证号,性别)等。
候选键:
候选键属于超键,它是最小的超键,就是说如果再去掉候选键中的任何一个属性它就不再是超键了。学生表中的候选键为:(学号)、(身份证号)。
主键:
主键就是候选键里面的一个,是人为规定的,例如学生表中,我们通常会让“学号”做主键,教师表中让“教师编号”做主键。
外键:
外键比较简单,学生表中的外键就是“教师编号”。外键主要是用来描述两个表的关系。
求候选键
将关系模式的函数依赖关系用“有向图”的方式表示。
找入度为0的属性,并以该属性集合为起点,尝试遍历有向图,若能正常遍历图中的所有结点,该属性集即为关系模式的个候选键。
若入度为0的属性集也不能遍历图中所有的结点,则需尝试性的将一些中间节点(既有入度,也有出度的结点)并入入度为0的属性集中,直至该集合能遍历所有结点,该集合为候选键。
例题:
1.用有向图表示后,A1的入度为0,从A1出发,沿A1-A2-A3-A2-A4发现可以遍历整个图,则A1为候选键。
2.用有向图表示后,ABDC的入度为0,候选键为ABCD的组合键,因为ABCD四个中的任意一个或几个键都不能遍历整个图,只有ABCD资格键的组合键才能遍历整个图。
注意:ABD→E和A→E、B→E、D→E的区别,前者是ABD的组合键可以确定E,后者是ABD中的任何一个都可以确定E,在有向图中的表示也有区别。
函数依赖
部分函数依赖:设X,Y是关系R的两个属性集合,存在X→Y,若X’是X的真子集,存在X’→Y,则称Y部分函数依赖于X。
举个例子:通过AB能得出C,通过A也能得出C,通过B也能得出C,那么说C部分依赖于AB。
完全函数依赖:设X,Y是关系R的两个属性集合,X’是X的真子集,存在X→Y,但对每一个X’都有X’!→Y,则称Y完全函数依赖于X。
举个例子:通过AB能得出C,但是AB单独得不出C,那么说C完全依赖于AB.
传递函数依赖:设X,Y,Z是关系R中互不相同的属性集合,存在X→Y(Y !→X),Y→Z,则称Z传递函数依赖于X。
举个例子:通过A得到B,通过B得到C,但是C得不到B,B得不到A,那么成C传递依赖于A
范式
1、第一范式(1NF):一个关系模式R的所有属性都是不可分的基本数据项。
2、第二范式(2NF):满足第一范式,然后消除部分依赖。
3、第三范式(3NF): 满足第二范式,消除传递依赖。
第一范式(1NF)
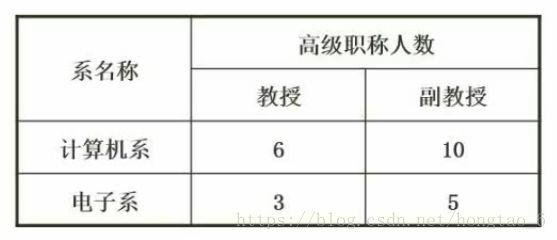
在关系模式R中,当且仅当所有域只包含原子值,即每个分量都是不可再分的数据项,则称R是第一范式。上表所示的关系R不满足1NF,因为高级职称可以拆分成教授和副教授。只需删除高级职称项即可满足1NF
第二范式(2NF)
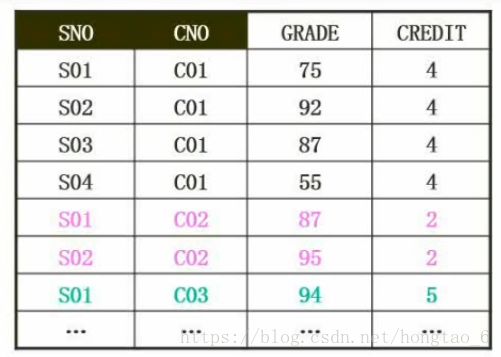
当且仅当R是1NF时,且满足每一个非主属性完全依赖主键(即不存在部分依赖)时,称R是第二范式。上表所示的关系R不满足2NF。SN0表示学号,CNO表示课程号,GRADE表示成绩,CREDIT表示学分。主键是学号和课程号的组合键,学号+课程号才能确定成绩。但是其存在部分依赖,即用学号可以确定学分,所以R不是2NF。
解决方案:在原关系R中删除CREDIT字段,再讲CNO与CREDIT重新组成一个新的关系。
第三范式(3NF)
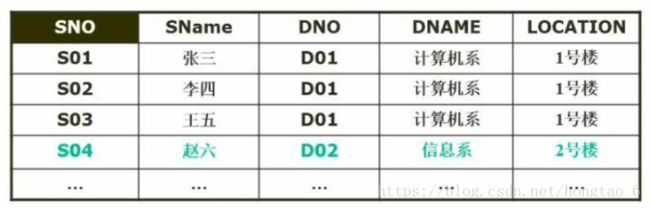
当且仅当R是2NF,且R中没有非主属性传递依赖码时,则称R是第三范式。解决方案:将DNO、DNAME、LOCATION从原来的关系删除并重新组成新的关系
鲍依斯-科得范式(BCNF)
消除主属性对候选键的传递依赖。设R是一个关系模式,F是它的依赖集,R属于BCNF当且仅当其F中每个依赖的决定因素必定包含R的某个候选码。简单来讲:符合3NF,并且,主属性不依赖于主属性
还可以这么说:若一个关系达到了第三范式,并且它只有一个候选码,或者它的每个候选码都是单属性,则该关系自然达到BC范式。
一般,一个数据库设计符合3NF或BCNF就可以了。
假设仓库管理关系表为StorehouseManage(仓库ID, 存储物品ID, 管理员ID, 数量),且有一个管理员只在一个仓库工作;一个仓库可以存储多种物品。这个数据库表中存在如下决定关系:
(仓库ID, 存储物品ID) →(管理员ID, 数量)
(管理员ID, 存储物品ID) → (仓库ID, 数量)
所以,(仓库ID, 存储物品ID)和(管理员ID, 存储物品ID)都是StorehouseManage的候选关键字,表中的唯一非关键字段为数量,它是符合第三范式的。但是,由于存在如下决定关系:
(仓库ID) → (管理员ID)
(管理员ID) → (仓库ID)
即存在关键字段决定关键字段的情况,所以其不符合BCNF范式。它会出现如下异常情况:
(1) 删除异常:
当仓库被清空后,所有”存储物品ID”和”数量”信息被删除的同时,”仓库ID”和”管理员ID”信息也被删除了。
(2) 插入异常:
当仓库没有存储任何物品时,无法给仓库分配管理员。
(3) 更新异常:
如果仓库换了管理员,则表中所有行的管理员ID都要修改。
把仓库管理关系表分解为二个关系表:
仓库管理:StorehouseManage(仓库ID, 管理员ID);
仓库:Storehouse(仓库ID, 存储物品ID, 数量)。
这样的数据库表是符合BCNF范式的,消除了删除异常、插入异常和更新异常。
模式分解无损连接
当范式级别不够的时候主要采取拆分模式的策略,拆分时需要考虑不同因素,有不同的原则。
保持函数依赖的分解:分解后函数依赖与分解前相同。比如R(A,B,C)存在函数依赖A→B,B→C,将R分解成R1(A,B),R2(B,C),此时R1保持A→B的函数依赖,R2保持B→C的函数依赖,所以R1和R2的分解是保持函数依赖分解。若R3(A,C),R1和R3的分解,不存在了B→C的函数依赖,所以R1,R3分解没有保持函数依赖。
无损联接分解:有损(不能还原),无损(可以还原)。将一个关系模式分解成若干个关系模式后,通过自然联接和投影等运算扔能还原到元老的关系模式。
判断无损分解:
方法一:
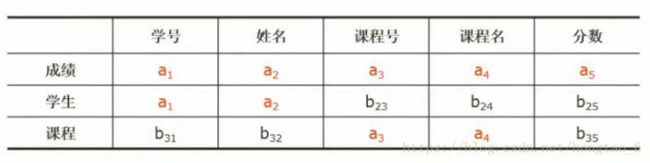
函数依赖:学号→姓名,课程号→课程名,(学号、课程号)→分数
原模式:成绩(学号,姓名,课程号,课程名,分数)
分解为:成绩(学号,课程号,分数);学生(学号,姓名);课程(课程号,课程名)
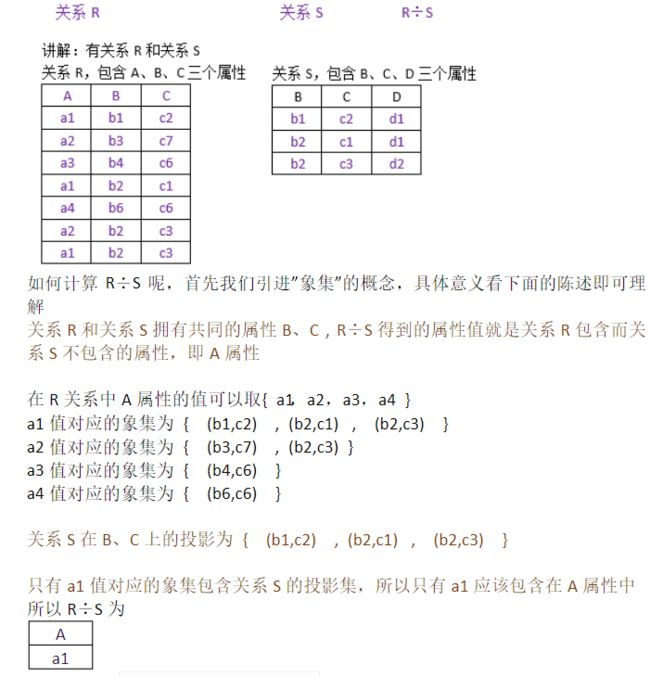
关系代数除法
数据库的传统集合运算(并、差、交、笛卡尔积)和专门的关系运算(选择、投影、连接、除运算
自然连接,等值连接,非等值连接
算术表达式中缀转后缀
给出一个中缀表达式如下:
a+bc-(d+e)
第一步:按照运算符的优先级对所有的运算单位加括号,
式子变成了:((a+(bc))-(d+e))
第二步:转换前缀与后缀表达式
前缀:把运算符号移动到对应的括号前面
则变成了:-( +(a (bc)) +(de))
把括号去掉:-+abc+de 前缀式子出现
后缀:把运算符号移动到对应的括号后面
则变成了:((a(bc)* )+ (de)+ )-
把括号去掉:abc*+de+- 后缀式子出现