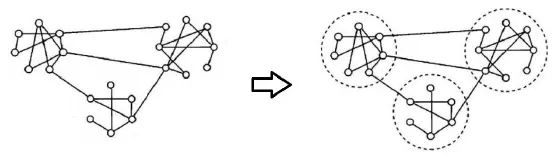
图论半监督学习需要首先构建一个图,图的节点集就是所有样本集( 包括标记样本和无标记 样本),图的边是样本两两间的相似性,然后把分类问题看作是类别信息在图上由标记节点向无标记节点的扩散或传播过程。
图论半监督学习
基于图的半监督学习核心思想就是给相似顶点尽可能赋予相同的标记,使得图的标记尽可能地平滑
标签传播算法
标签传播算法(Label Propagation Algorithm)是图论半监督学习的主要代表,基本思路是从已标记的节点的标签信息来预测未标记的节点的标签信息,利用样本间的关系,建立完全图模型。
每个节点标签按相似度传播给相邻节点,在节点传播的每一步,每个节点根据相邻节点的标签来更新自己的标签,与该节点相似度越大,其相邻节点对其标注的影响权值越大,相似节点的标签越趋于一致,其标签就越容易传播。在标签传播过程中,保持已标记的数据的标签不变,使其将标签传给未标注的数据。最终当迭代结束时,相似节点的概率分布趋于相似,可以划分到一类中。
1、sklearn版本
# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn.semi_supervised import LabelPropagation
from sklearn.datasets.samples_generator import make_classification
from sklearn.externals import joblib
class LP(object):
def __init__(self, kernel='rbf'):
self.kernel = kernel
def train(self, X, Y_train):
self.clf = LabelPropagation(max_iter=100, kernel=self.kernel, gamma=0.1)
self.clf.fit(X, Y_train)
def score(self, X, Y):
return self.clf.score(X, Y)
def predict(self, X):
return self.clf.predict(X)
def save(self, path='./LP.model'):
joblib.dump(self.clf, path)
def load(self, model_path='./LP.model'):
self.clf = joblib.load(model_path)
if __name__ == '__main__':
features, labels = make_classification(n_samples=200, n_features=3, n_redundant=1, n_repeated=0, n_informative=2, n_clusters_per_class=2)
n_given = 70
# 取前n_given个数字作为标注集
index = np.arange(len(features))
X = features[index]
Y = labels[index]
unlabeled_index = np.arange(len(Y))[n_given:]
Y_train = np.copy(Y)
Y_train[unlabeled_index] = -1
LP = LP()
LP.train(X, Y_train)
print(LP.predict(X[unlabeled_index]))
print(LP.score(X[unlabeled_index], Y[unlabeled_index]))
2、源码版本
# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
class LP(object):
def __init__(self, kernel='rbf'):
self.kernel = kernel
def buildGraph(self, X, rbf_sigma):
Graph = np.zeros((len(X), len(X)), np.float32)
for i in range(len(X)):
row_sum = 0.0
for j in range(len(X)):
diff = X[i, :] - X[j, :]
Graph[i][j] = np.exp(sum(diff**2) / (-2.0 * rbf_sigma **2))
row_sum += Graph[i][j]
Graph[i][:] /= row_sum
return Graph
def main(self, X1, X2, Y1, rbf_sigma=1.5, max_iter = 500):
N = len(X1) + len(X2)
num_classes = len(np.unique(Y1))
X = np.vstack((X1, X2))
label_known = np.zeros((len(X1), num_classes), np.float32)
for i in range(len(X1)):
label_known[i][Y1[i]] = 1.0
label_function = np.zeros((N, num_classes), np.float32)
label_function[:len(X1)] = label_known
label_function[len(X1):] = -1.0
# 构建图
Graph = self.buildGraph(X, rbf_sigma)
# 开始传播
iter = 0
pre_label_function = np.zeros((N, num_classes), np.float32)
changed = np.abs(pre_label_function - label_function).sum()
while iter < max_iter and changed > 1e-3:
if iter % 1 == 0:
print("---> Iteration %d/%d, changed: %f" % (iter, max_iter, changed))
pre_label_function = label_function
iter += 1
# 传播
label_function = np.dot(Graph, label_function)
label_function[:len(X1)] = label_known
changed = np.abs(pre_label_function - label_function).sum()
unlabel_data_labels = np.zeros(len(X2))
for i in range(len(X2)):
unlabel_data_labels[i] = np.argmax(label_function[i+len(X1)])
return unlabel_data_labels
if __name__ == '__main__':
features, labels = make_classification(n_samples=200, n_features=3, n_redundant=1, n_repeated=0, n_informative=2, n_clusters_per_class=2)
n_given = 100
# 取前n_given个数字作为标注集
index = np.arange(len(features))
X = features[index]
Y = labels[index]
X1 = np.copy(X)[:n_given]
X2 = np.copy(X)[n_given:]
Y1 = np.copy(Y)[:n_given]
LP = LP()
print(LP.main(X1, X2, Y1))
print(np.copy(Y)[n_given:])