转载自:https://blog.csdn.net/qq_33935254/article/details/55505472
1 Trie树
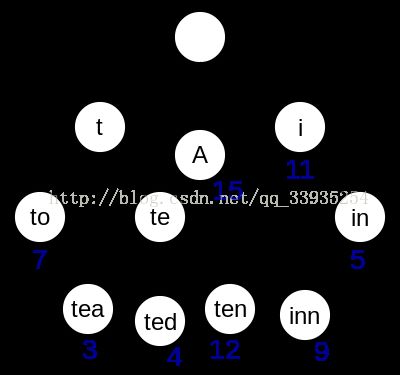
Trie树,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
在图示中,键标注在节点中,值标注在节点之下。每一个完整的英文单词对应一个特定的整数。键不需要被显式地保存在节点中。图示中标注出完整的单词,只是为了演示trie的原理。trie中的键通常是字符串,但也可以是其它的结构。
上图是一个简略视图,实际上trie每个节点是一个确定长度的数组,数组中每个节点的值是一个指向子节点的指针,最后有个标志域,标识这个位置为止是否是一个完整的字符串,并且有几个这样的字符串
常见的用来存英文单词的trie每个节点是一个长度为27的指针数组,index0-25代表a-z字符,26为标志域。如图:
2 Patricia树
Patricia树,或称Patricia trie,或crit bit tree,压缩前缀树,是一种更节省空间的Trie。对于基数树的每个节点,如果该节点是唯一的儿子的话,就和父节点合并。
3 Merkle树
Merkle Tree,通常也被称作Hash Tree,顾名思义,就是存储hash值的一棵树。Merkle树的叶子是数据块(例如,文件或者文件的集合)的hash值。非叶节点是其对应子节点串联字符串的hash。(不懂Hash运算的可以自行百度)
要了解Merkle Tree就要先从Hash List说起:
怎么确定小的数据块没有损坏哪?只需要为每个数据块做Hash。BT下载的时候,在下载到真正数据之前,我们会先下载一个Hash列表。那么问题又来了,怎么确定这个Hash列表本事是正确的哪?答案是把每个小块数据的Hash值拼到一起,然后对这个长字符串在作一次Hash运算,这样就得到Hash列表的根Hash(Top Hash or Root Hash)。下载数据的时候,首先从可信的数据源得到正确的根Hash,就可以用它来校验Hash列表了,然后通过校验后的Hash列表校验数据块。
Merkle Tree可以看做Hash List的泛化(Hash List可以看作一种特殊的Merkle Tree,即树高为2的多叉Merkle Tree。
在最底层,和哈希列表一样,我们把数据分成小的数据块,有相应地哈希和它对应。但是往上走,并不是直接去运算根哈希,而是把相邻的两个哈希合并成一个字符串,然后运算这个字符串的哈希,这样每两个哈希就结婚生子,得到了一个”子哈希“。如果最底层的哈希总数是单数,那到最后必然出现一个单身哈希,这种情况就直接对它进行哈希运算,所以也能得到它的子哈希。于是往上推,依然是一样的方式,可以得到数目更少的新一级哈希,最终必然形成一棵倒挂的树,到了树根的这个位置,这一代就剩下一个根哈希了,我们把它叫做 Merkle Root。
在p2p网络下载网络之前,先从可信的源获得文件的Merkle Tree树根。一旦获得了树根,就可以从其他从不可信的源获取Merkle tree。通过可信的树根来检查接受到的MerkleTree。如果Merkle Tree是损坏的或者虚假的,就从其他源获得另一个Merkle Tree,直到获得一个与可信树根匹配的MerkleTree。
Merkle Tree和HashList的主要区别是,可以直接下载并立即验证Merkle Tree的一个分支。因为可以将文件切分成小的数据块,这样如果有一块数据损坏,仅仅重新下载这个数据块就行了。如果文件非常大,那么Merkle tree和Hash list都很到,但是Merkle tree可以一次下载一个分支,然后立即验证这个分支,如果分支验证通过,就可以下载数据了。而Hash list只有下载整个hash list才能验证。
4 MPT(Merkle Patricia Tree)树
知道了Merkle Tree,知道了Patricia Tree,顾名思义,MPT(Merkle Patricia Tree)就是这两者混合后的产物。
在以太坊(ethereum)中,使用了一种特殊的十六进制前缀(hex-prefix, HP)编码,所以在字母表中就有16个字符。这其中的一个字符为一个nibble。
MPT树中的节点包括空节点、叶子节点、扩展节点和分支节点:
空节点,简单的表示空,在代码中是一个空串。
叶子节点(leaf),表示为[key,value]的一个键值对,其中key是key的一种特殊十六进制编码,value是value的RLP编码。
扩展节点(extension),也是[key,value]的一个键值对,但是这里的value是其他节点的hash值,这个hash可以被用来查询数据库中的节点。也就是说通过hash链接到其他节点。
分支节点(branch),因为MPT树中的key被编码成一种特殊的16进制的表示,再加上最后的value,所以分支节点是一个长度为17的list,前16个元素对应着key中的16个可能的十六进制字符,如果有一个[key,value]对在这个分支节点终止,最后一个元素代表一个值,即分支节点既可以搜索路径的终止也可以是路径的中间节点。
MPT树中另外一个重要的概念是一个特殊的十六进制前缀(hex-prefix, HP)编码,用来对key进行编码。因为字母表是16进制的,所以每个节点可能有16个孩子。因为有两种[key,value]节点(叶节点和扩展节点),引进一种特殊的终止符标识来标识key所对应的是值是真实的值,还是其他节点的hash。如果终止符标记被打开,那么key对应的是叶节点,对应的值是真实的value。如果终止符标记被关闭,那么值就是用于在数据块中查询对应的节点的hash。无论key奇数长度还是偶数长度,HP都可以对其进行编码。最后我们注意到一个单独的hex字符或者4bit二进制数字,即一个nibble。
HP编码很简单。一个nibble被加到key前(下图中的prefix),对终止符的状态和奇偶性进行编码。最低位表示奇偶性,第二低位编码终止符状态。如果key是偶数长度,那么加上另外一个nibble,值为0来保持整体的偶特性。
如图所示:
总共有2个扩展节点,2个分支节点,4个叶子节点。
其中叶子结点的键值情况为:
节点的前缀:
5 MPT树的操作
下面从MPT树的更新,删除和查找过程来说明MPT树的操作。
1 更新
函数_update_and_delete_storage(self, node, key, value)
i. 如果node是空节点,直接返回[pack_nibbles(with_terminator(key)), value],即对key加上终止符,然后进行HP编码。
ii. 如果node是分支节点,如果key为空,则说明更新的是分支节点的value,直接将node[-1]设置成value就行了。如果key不为空,则递归更新以key[0]位置为根的子树,即沿着key往下找,即调用_update_and_delete_storage(self._decode_to_node(node[key[0]]),key[1:], value)。
iii. 如果node是kv节点(叶子节点或者扩展节点),调用_update_kv_node(self, node, key, value),见步骤iv
iv. curr_key是node的key,找到curr_key和key的最长公共前缀,长度为prefix_length。Key剩余的部分为remain_key,curr_key剩余的部分为remain_curr_key。
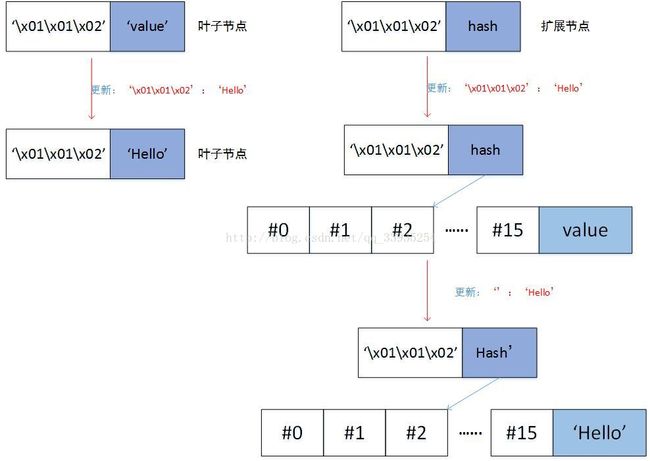
a) 如果remain_key==[]== remain_curr_key,即key和curr_key相等,那么如果node是叶子节点,直接返回[node[0], value]。如果node是扩展节点,那么递归更新node所链接的子节点,即调用_update_and_delete_storage(self._decode_to_node(node[1]),remain_key, value)
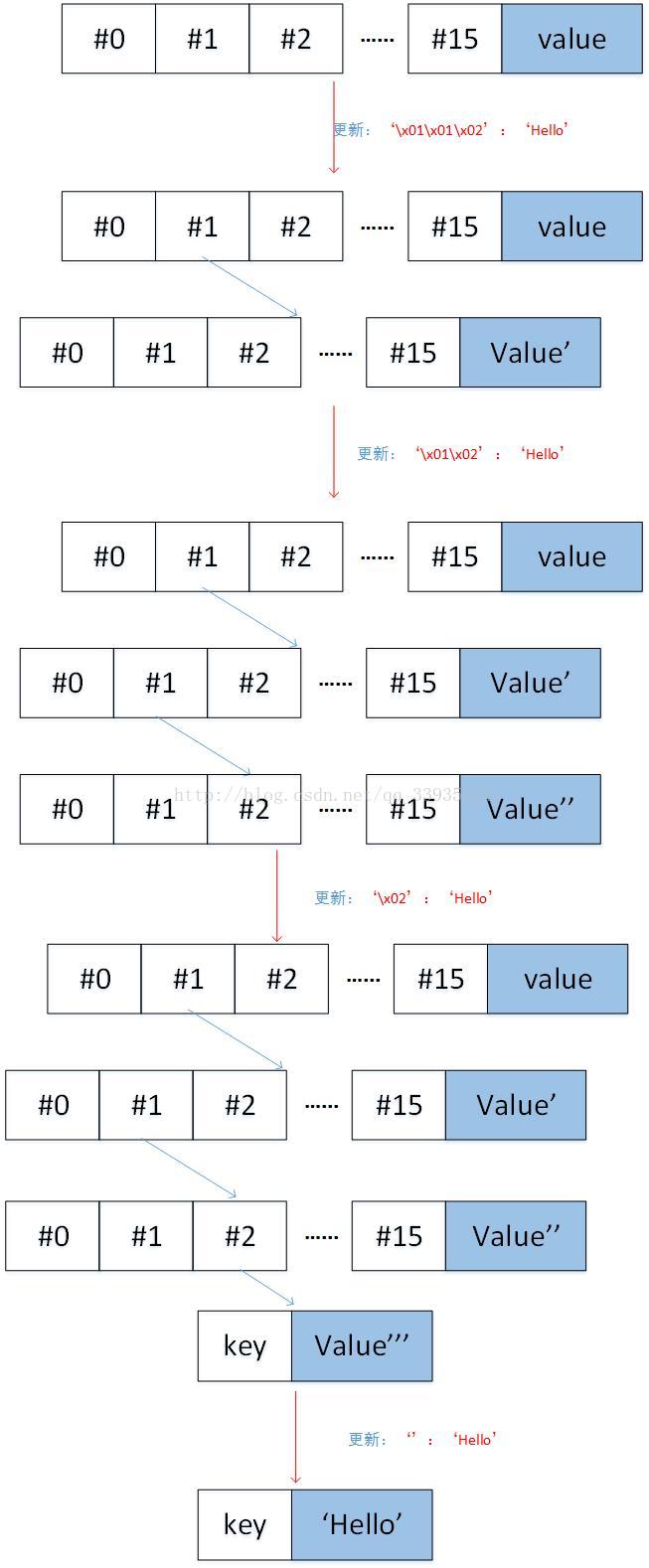
b) 如果remain_curr_key == [],即curr_key是key的一部分。如果node是扩展节点,递归更新node所链接的子节点,即调用_update_and_delete_storage(self._decode_to_node(node[1]),remain_key, value);如果node是叶子节点,那么创建一个分支节点,分支节点的value是当前node的value,分支节点的remain_key[0]位置指向一个叶子节点,这个叶子节点是[pack_nibbles(with_terminator(remain_key[1:])),value]
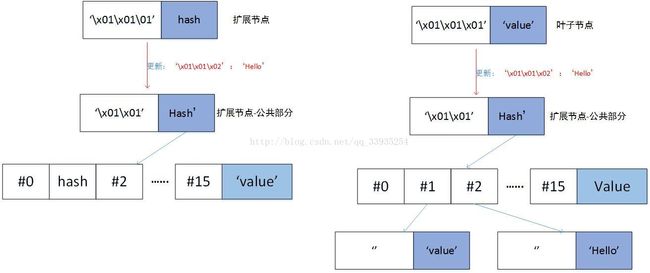
c) 否则,创建一个分支节点。如果curr_key只剩下了一个字符,并且node是扩展节点,那么这个分支节点的remain_curr_key[0]的分支是node[1],即存储node的value。否则,这个分支节点的remain_curr_key[0]的分支指向一个新的节点,这个新的节点的key是remain_curr_key[1:]的HP编码,value是node[1]。如果remain_key为空,那么新的分支节点的value是要参数中的value,否则,新的分支节点的remain_key[0]的分支指向一个新的节点,这个新的节点是[pack_nibbles(with_terminator(remain_key[1:])),value]
d) 如果key和curr_key有公共部分,为公共部分创建一个扩展节点,此扩展节点的value链接到上面步骤创建的新节点,返回这个扩展节点;否则直接返回上面步骤创建的新节点
v. 删除老的node,返回新的node
l 删除
删除的过程和更新的过程类似,而且很简单,函数名:_delete_and_delete_storage(self, key)
i. 如果node为空节点,直接返回空节点
ii. 如果node为分支节点。如果key为空,表示删除分支节点的值,直接另node[-1]=‘’, 返回node的正规化的结果。如果key不为空,递归查找node的子节点,然后删除对应的value,即调用self._delete_and_delete_storage(self._decode_to_node(node[key[0]]),key[1:])。返回新节点
iii. 如果node为kv节点,curr_key是当前node的key。
a) 如果key不是以curr_key开头,说明key不在node为根的子树内,直接返回node。
b) 否则,如果node是叶节点,返回BLANK_NODE if key == curr_key else node。
c)如果node是扩展节点,递归删除node的子节点,即调用_delete_and_delete_storage(self._decode_to_node(node[1]),key[len(curr_key):])。如果新的子节点和node[-1]相等直接返回node。否则,如果新的子节点是kv节点,将curr_key与新子节点的可以串联当做key,新子节点的value当做vlaue,返回。如果新子节点是branch节点,node的value指向这个新子节点,返回。
l 查找
查找操作更简单,是一个递归查找的过程函数名为:_get(self, node, key)
i. 如果node是空节点,返回空节点
ii. 如果node是分支节点,如果key为空,返回分支节点的value;否则递归查找node的子节点,即调用_get(self._decode_to_node(node[key[0]]), key[1:])
iii. 如果node是叶子节点,返回node[1] if key == curr_key else ‘’
iv. 如果node是扩展节点,如果key以curr_key开头,递归查找node的子节点,即调用_get(self._decode_to_node(node[1]),key[len(curr_key):]);否则,说明key不在以node为根的子树里,返回空