最近一直在做系统方面的研发和前沿技术探索工作,较少接触算法方面的工作,故而有些生疏。为此,利用工作之余重新阅读算法导论(Introduction to Algorithms)一书,重新回顾算法相关的知识。所谓温故而知新,不亦说乎。为了方便以后复习方便,故做此笔记。
排序算法
问题描述
输入:包含n个数字的序列[a1, a2, ..., an]
输出:重排序的序列[a1', a2', ..., an'],使得a1'≤a2'≤...≤an'.
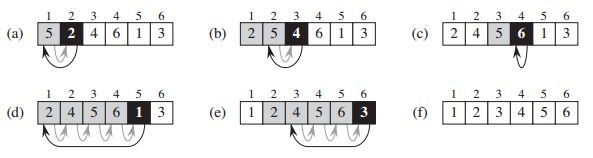
插入排序
对于少量元素的排序,插入排序算法是高效的。
核心思想
与排序扑克牌的方式类似:
- 开始时,左手为空,牌面朝下放在桌上
- 每次从桌上拿出一张牌,并插入左手中的适当位置
- 为了找出该牌的正确位置,自右向左与手中的每张牌比较
- 左手中的牌总是有序的,这些牌最初位于桌上牌堆的顶部
伪代码
INSERT-SORT(A)
for j = 2 to A.length
key = A[j]
// 将A[j]插入到已排序序列A[1..j-1]
i = j - 1
while i > 0 and A[i] > key
A[i + 1] = A[i]
i = i - 1
A[i+1] = key
这里,A[1..n]为待排序序列,A.length表示序列的长度(n)。
C代码
// 输入:a为待排序数组,n为元素数目
void insert_sort(int *a, int n) {
for(int j = 1; j < n; j++) {
int key = a[j];
int i = j - 1;
while(i >= 0 && a[i] > key) {
a[i + 1] = a[i];
i--;
}
a[i + 1] = key;
}
}
特性
- 最坏情形复杂度(序列逆序排列):θ(n2) [笔者注:运行时间an2+bn+c]
- 最好情形复杂度(序列已经排序):& theta;(n)[笔者注:运行时间an+b]
- 平均复杂度:θ(n2)
- 算法是稳定的(排序前后关键字相同的两个元素相对位置不变)
选择排序
核心思想
待排序数组A[1,...,n],A.length表示数组的长度。首选,选择数组A的最小元素,并将其与A[1]交换。然后,选择数组的次小元素,并将其与A[2]交换。对数组元素A[1,...,n-1]执行上述过程。
伪代码
SELECTION-SORT(A)
n = A.length
for j = 1 to n - 1
smallest = j
for i = j + 1 to n
if A[i] < A[smallest]
smallest = i
exchange A[j] with A[smallest]
C代码
// 输入:a为待排序数组,n为元素数目
void selection_sort(int *a, int n) {
for(int j = 0; j < n - 1; j++) {
int smallest = j;
for(int i = j + 1; i < n; i++) {
if(a[i] < a[smallest])
smallest = i;
}
int temp = a[smallest];
a[smallest] = a[j];
a[j] = temp;
}
}
特性
- 运行时间与输入的状态无关,即最好和最坏情形复杂度均为:θ(n2)
- 算法是稳定的(排序前后相同的两个元素相对位置不变)
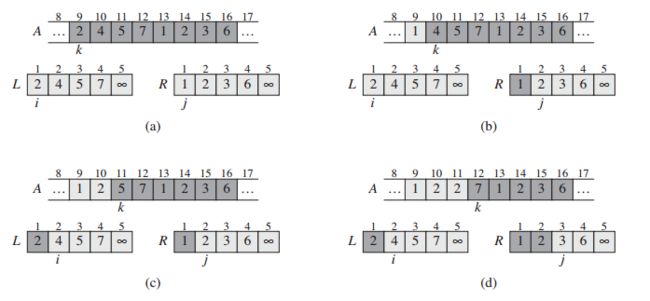
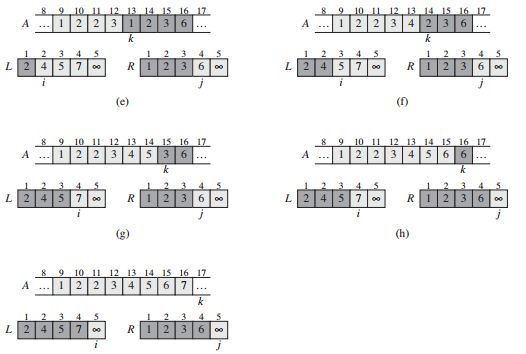
归并排序
核心思想
待排序数组A[1,...,n],A.length表示数组的长度。首选,将待排序序列划分为两个子序列,长度为n/2。然后,使用归并排序递归排序两个子序列。最后,归并两个已排序子序列,从而生成排序序列。
伪代码
MERGE(A, p, q, r)
n1 = q - p + 1
n2 = r - q
let L[1..n1+1] and R[1..n2+2]为新数组
for i = 1 to n1
L[i] = A[p + i - 1]
for j = 1 to n2
R[j] = A[q+j]
L[n1+1] = INF
R[n2+1] = INF
i = 1
j = 1
for k = p to r
if L[i] <= R[j]
A[k] = L[i]
i = i + 1
else
A[k] = R[j]
j = j + 1
MERGE-SORT(A, p, r)
if p < r
q = (p + r) / 2
MERGE_SORT(A, p, q)
MERGE_SORT(A, q + 1, r)
MERGE(A, p, q, r)
C代码
// 输入:a为待排序数组
void merge(int *a, int p, int q, int r) {
int n1 = q - p + 1;
int n2 = r - q;
int *L = new int[n1];
int *R = new int[n2];
for(int i = 0; i < n1; i++) {
L[i] = a[p + i];
}
for(int j = 0; i < n2; j++) {
R[j] = a[q + j + 1];
}
int i = 0;
int j = 0;
int k = p;
while(i < n1 && j < n2) {
if(L[i] <= R[j]) {
a[k++] = L[i++];
} else {
a[k++] = R[j++];
}
}
while(i < n1) {
a[k++] = L[i++];
}
while(j < n2) {
a[k++] = R[j++];
}
}
void merge_sort(int *a, int p, int r) {
if(p < r) {
int q = (p + r) / 2;
merge_sort(a, p, q);
merge_sort(a, q + 1, r);
merge(a, p, q, r);
}
}
特性
- 运行时间与输入的状态无关,即最好和最坏情形复杂度均为:θ(nlgn)
- 算法是稳定的(排序前后相同的两个元素相对位置不变)
折半查找
核心思想
已排序数组A[1,...,n],A.length表示数组的长度。首选,与数组中间的元素进行比较,如果相等则查找结束。如果中间元素值小于待查找值,则在数组右半部分进行查找;否则,在数组的左半边部分进行查找。
伪代码
ITERATIVE-BINARY_SEARCH(A, v, low, high)
while low <= high
mid = (low + high) / 2
if v = A[mid]
return mid
if v > A[mid]
low = mid + 1
else
high = mid - 1
return NIL
RECURSIVE-BINARY-SEARCH(A, v, low, high)
if low > high
return NIL
mid = (low + high) / 2
if v = A[mid]
return mid
if v > A[mid]
return RECURSIVE-BINARY-SEARCH(A, v, mid + 1, high)
else
return RECURSIVE-BINARY-SEARCH(A, v, low, mid - 1)
C代码
int iterative_binary_search(int *a, int v, int low, int high) {
while(low <= high) {
int mid = (low + high) / 2;
if(a[mid] == v)
return mid;
else if(a[mid] > v)
high = mid - 1;
else
low = mid + 1;
}
return -1;
}
int recursive_binary_search(int *a, int v, int low, int high) {
if(low > high)
return -1;
int mid = (low+high) / 2;
if(a[mid] == v)
return mid;
if(v < a[mid])
return recursive_binary_search(a, v, low, mid - 1);
else
return recursive_binary_search(a, v, mid + 1, high);
}
冒泡排序
核心思想
自右向左遍历数组,不断交换两个元素使最小元素向左方移动,最终,A[0]为最小元素。接着,重复上述过程,A[1]为次小元素。对A[2..n]重复上述过程。
伪代码
BUBBLE-SORT(A)
for i = 1 to A.length - 1
for j = A.length downto i + 1
if(A[j] < A[j - 1]
exchange A[j] with A[j - 1]
C代码
// 输入:a为待排序数组,n为元素数目
void bubble_sort(int *a, int n) {
for(int i = 0; i < n - 1; i++) {
for(int j = n - 1; j > i; j--) {
if(a[j] < a[j - 1]) {
int temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
}
}
}
}
特性
- 运行时间与输入的状态无关,即最好和最坏情形复杂度均为:θ(n2)
- 算法是稳定的(排序前后相同的两个元素相对位置不变)
常见排序算法比较
由于其内层循环非常紧凑,对于小规模输入,插入排序是一种非常快的原址排序(in place)。归并排序由更好的渐进运行时间,但它所使用的MERGE过程并不是原址的。在实际应用中,快速排序通常比堆排序快。与插入排序类似,快速排序的代码也很紧凑,因此运行时间中隐含的常数系数非常小。快速排序是排序大数组的最常用算法。