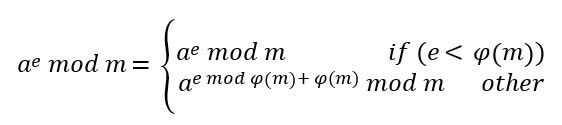模运算
POJ 1150: The Last Non-zero Digit
题解链接 https://blog.csdn.net/Avalon_cc/article/details/79967855
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
题解链接 https://blog.csdn.net/Avalon_cc/article/details/79967855
*/
#include
#include
#include
#include
#include
#include
POJ 1284: Primitive Roots
求原根个数的模板题。
定理:如果p有原根,则它恰有φ(φ(p))个不同的原根(无论p是否为素数都适用)
p为素数,当然φ(p)=p-1,因此就有φ(p-1)个原根。
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
求原根个数的模板题。
定理:如果p有原根,则它恰有φ(φ(p))个不同的原根(无论p是否为素数都适用)
p为素数,当然φ(p)=p-1,因此就有φ(p-1)个原根。
*/
#include
#include
#include
#include
#include
#include
POJ 2115: C Looooops
可以求,同时x和y的值就是的一组解。
对于该题,相当于求关于x的同余方程的最小整数解。
对上式变形得,。即。
设。根据裴蜀定理,若(B-A)%d==0,则原方程有整数解。
于是先特判是否有解后,在方程两遍同除以d(模数也要除以d)。
最后将exgcd算出的x乘以然后再对求模即可。
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
d=exgcd(a,b,x,y)可以求gcd(a,b)=d,同时x和y的值就是ax+by=1的一组解。
对于该题,相当于求关于x的同余方程A+xC≡B(mod 2^k)的最小整数解。
对上式变形得,A+xC=B-y*2^k。即xC+y*2^k=B-A。
设d=gcd(C,2^k)。根据裴蜀定理,若(B-A)%d==0,则原方程有整数解。
于是先特判是否有解后,在方程两遍同除以d(模数也要除以d)。
最后将exgcd算出的x乘以(B-A)/d然后再对2^k/d求模即可。
*/
#include
#include
#include
#include
#include
#include
POJ 3708: Recurrent Function
题解链接 http://www.hankcs.com/program/algorithm/poj-3708-recurrent-function.html
模数和底数不一定互质,所以需要应用多次欧几里得算法。
除此之外,还需要高精度,不想打。
代码如下
POJ 2720: Last Digits
题解链接 https://blog.csdn.net/yuege38/article/details/78989456
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
题解链接 https://blog.csdn.net/yuege38/article/details/78989456
http://ww3.sinaimg.cn/large/6cbb8645jw1es7p9f2l68j20fm03hdfx.jpg
*/
#include
#include
#include
#include
#include
#include
#define int long long
#define re register
using namespace std;
typedef long long ll;
const int maxn=100+5;
int base[10]= {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000};
int tab[maxn][maxn]; //tab[i,j]表示i^i^i...^i(j个i)是否>1e7,是则为-1,否则为i^i^i...^i(j个i)的确切值/上次计算过的答案(用于开始时的判断)
int fxb[maxn][maxn]; //fxb[i,j]表示i^i^i...^i(j个i)是否>1e7,否则为i^i^i...^i(j个i)的确切值(用于欧拉定理时的递归计算时的判断)
inline int limit_power(int a,int b) {
ll res=1;
for(int i=1; i<=b; ++i) {
res=res*1ll*a;
if(res>1e7) return -1;
}
return res;
}
void init() {
memset(tab,-1,sizeof(tab));
memset(fxb,-1,sizeof(fxb));
for(int i=1; i<=maxn-5; ++i) {
tab[i][0]=fxb[i][0]=1;
for(int j=1; j<=maxn-5; ++j) {
tab[i][j]=fxb[i][j]=limit_power(i,fxb[i][j-1]);
if(tab[i][j]==-1) break;
}
}
}
inline ll ksm(int x,int b,int mod) {
ll res=1;
while(b) {
if(b&1) res=res*x%mod;
x=x*x%mod;
b>>=1;
}
return res;
}
inline int get_phi(int x) {
int ans=x;
for(int i=2; i*i<=x; ++i) {
if(x%i==0) {
ans=ans/i*(i-1);
while(x%i==0) x/=i;
}
}
if(x>1) ans=ans/x*(x-1);
return ans;
}
/*
int solve(int b,int a,int mod) {
if(fxb[b][a]!=-1) return fxb[b][a]%mod;//
int phi=get_phi(mod);
if(fxb[b][a-1]!=-1&&fxb[b][a-1]<=phi) return ksm(b,fxb[b][a-1],mod);
return ksm(b,solve(b,a-1,phi)+phi,mod);
}
*/
int solve(int b,int x,int mod) {
if(fxb[b][x]==-1) {
int phi=get_phi(mod);
if(fxb[b][x-1]!=-1&&fxb[b][x-1]
矩阵
POJ 2345: Central heating
代码如下
/*
题意:有n个窗口,有n个师傅,每个师傅可以管理很多窗口,可以重复的,给一个师傅下命令,
这个师傅会管理他所有的窗口,如果是关闭的就打开,如果是打开的就关闭,现在想让所有的窗口打开,问你怎么下命令。
思路:将每个师傅管理的窗口转化成01序列,末尾加0,表示方程的结果,然后凑成矩阵,高斯消元解方程,消元的时候变成异或。
*/
#include
#include
#include
#include
#include
#include
POJ 3532: Resistance
在电路中,很难直接根据输入判断每条导线中电流的流向。
因此需要基尔霍夫定律来列出每个点电位的方程。
具体题解链接
https://blog.csdn.net/yuege38/article/details/78946445
http://m.bubuko.com/infodetail-1987259.html
代码如下
/*
在电路中,很难直接根据输入判断每条导线中电流的流向。
因此需要基尔霍夫定律来列出每个点电位的方程。
具体题解链接
https://blog.csdn.net/yuege38/article/details/78946445
http://m.bubuko.com/infodetail-1987259.html
*/
#include
#include
#include
#include
#include
#include
POJ 3526: The Teacher’s Side of Math
根据每个无理项的系数和为0(最高项系数和为1)来列方程求解。
题解链接 https://blog.csdn.net/FSAHFGSADHSAKNDAS/article/details/89089005
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
根据每个无理项a^{x/m}b^{y/n}的系数和为0(最高项系数和为1)来列方程求解。
题解链接 https://blog.csdn.net/FSAHFGSADHSAKNDAS/article/details/89089005
*/
#include
#include
#include
#include
#include
#include
计数
POJ 2407: Relatives
欧拉函数裸题,不再赘述。
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
欧拉函数裸题,不再赘述。
*/
#include
#include
#include
#include
#include
#include
POJ 1286: Necklace of Beads
与POJ2049相仿,不再赘述。
注意考虑s=0的情况,需要输出0,直接跑会RE。
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
与POJ2049相仿,不再赘述。
注意考虑s=0的情况,需要输出0,直接跑会RE。
*/
#include
#include
#include
#include
#include
#include
POJ 2409: Let it Bead
书上原题,需要额外考虑翻转的情况。
题解链接 http://hzwer.com/6861.html
代码如下
/*
*/
#define method_1
#ifdef method_1
/*
书上原题,需要额外考虑翻转的情况。
题解链接 http://hzwer.com/6861.html
*/
#include
#include
#include
#include
#include
#include