现将小生研一数值分析作业摘录如下,上机的代老师要求我们分为四个部分:解题理论依据、计算程序、计算结果截图和问题讨论,因公式输入不便所以第一部分的公式略去,需要的可去下载附件。因为本人编程水平有限,故使用的是最基本的函数,但保证原创和结果正确,所有程序在VC++6.0上验证通过,还望各位兄台不吝赐教。
第一题(二问):超松弛法求方程组根
1.解题理论依据或方法应用条件:
超松弛算法是在GS方法已求出x(m),x(m-1)的基础上,经过重新组合得到新序列。如能恰当选择松弛因子ω,收敛速度会比较快。当ω>1时,称为超松弛法,可以用来加速收敛。
2.计算程序(使用软件:VC):
#include
#define w 1.4
main()
{float a[10][10]={ {0,0,0,0,0,0,0,0,0,0},
{0,12.38412,2.115237,-1.061074,1.112336,-0.113584,0.718719,1.742382,3.067813,-2.031743},
{0,2.115237,19.141823,-3.125432,-1.012345,2.189736,1.563849,-0.784165,1.112348,3.123124},
{0,-1.061074,-3.125432,15.567914,3.123848,2.031454,1.836742,-1.056781,0.336993,-1.010103},
{0,1.112336,-1.012345,3.123848,27.108437,4.101011,-3.741856,2.101023,-0.71828,-0.037585},
{0,-0.113584,2.189736,2.031454,4.101011,19.897918,0.431637,-3.111223,2.121314,1.784317},
0,0.718719,1.563849,1.836742,-3.741856,0.431637,9.789365,-0.103458,-1.103456,0.238417},
{0,1.742382,-0.784165,-1.056781,2.101023,-3.111223,-0.103458,14.7138465,3.123789,-2.213474},
{0,3.067813,1.112348,0.336993,-0.71828,2.121314,-1.103456,3.123789,30.719334,4.446782},
{0,-2.031743,3.123124,-1.010103,-0.037585,1.784317,0.238417,-2.213474,4.446782,40.00001}};
float b[10][1]=
{{0},{2.1874369},{33.992318},{-25.173417},{0.84671695},{1.784317},{-86.612343},{1.1101230},{4.719345},{-5.6784392}};
float x[10][10]={{0},{0},{0},{0},{0},{0},{0},{0},{0},{0}}; /*由x(0)=0得到其第一列全为零*/
float sum1=0,sum2=0;
int i,m,j;
for(m=1;m<=9;m++)
for(i=1;i<=9;i++)
{sum1=0;
for(j=1;j<=(i-1);j++)sum1+=(-a[i][j]/a[i][i])*x[j][m]; /*计算第一个累加和*/
sum2=0;
for(j=(i+1);j<=9;j++)sum2+=(-a[i][j]/a[i][i])*x[j][m-1]; /*计算第二个累加和*/
x[i][m]=(1-w)*x[i][m-1]+w*(sum1+sum2+b[i][0]/a[i][i]); /*用SOR方法计算*/
}
printf("x1为:%lf\n",x[1][9]);
printf("x2为:%lf\n",x[2][9]);
printf("x3为:%lf\n",x[3][9]);
printf("x4为:%lf\n",x[4][9]);
printf("x5为:%lf\n",x[5][9]);
printf("x6为:%lf\n",x[6][9]);
printf("x7为:%lf\n",x[7][9]);
printf("x8为:%lf\n",x[8][9]);
printf("x9为:%lf\n",x[9][9]);
}
3.计算结果
4.问题讨论(误差分析、上机出现情况等)
这道题目是所有题目中编写最顺利的,一次即顺利得出结果,当然这道题目还是有应该注意到地方,一是注意两个求和的清零,二是注意下标,不要弄混行标和列标。
第一题(三问):列主元素法求方程组根
1.解题理论依据或方法应用条件:
所谓列主元消去法是,对矩阵作恰当的调整,选取绝对值最大的元素作为主元素。然后把矩阵化为上三角阵,再进行回代,求出方程的解。
2.计算程序(使用软件:VC):
#include
#include
main()
{double a[10][11]={ {0,0,0,0,0,0,0,0,0,0,0},
{0,12.38412,2.115237,-1.061074,1.112336,-0.113584,0.718719,1.742382,3.067813,-2.031743,2.1874369},
{0,2.115237,19.141823,-3.125432,-1.012345,2.189736,1.563849,-0.784165,1.112348,3.123124,33.992318},
{0,-1.061074,-3.125432,15.567914,3.123848,2.031454,1.836742,-1.056781,0.336993,-1.010103,-25.173417},
{0,1.112336,-1.012345,3.123848,27.108437,4.101011,-3.741856,2.101023,-0.71828,-0.037585,0.84671695},
{0,-0.113584,2.189736,2.031454,4.101011,19.897918,0.431637,-3.111223,2.121314,1.784317,1.784317},
{0,0.718719,1.563849,1.836742,-3.741856,0.431637,9.789365,-0.103458,-1.103456,0.238417,-86.612343},
{0,1.742382,-0.784165,-1.056781,2.101023,-3.111223,-0.103458,14.7138465,3.123789,-2.213474,1.1101230},
{0,3.067813,1.112348,0.336993,-0.71828,2.121314,-1.103456,3.123789,30.719334,4.446782,4.719345},
{0,-2.031743,3.123124,-1.010103,-0.037585,1.784317,0.238417,-2.213474,4.446782,40.00001,-5.6784392}};
double x[10],y[11];
double sum=0,max;
int i,j,j1,m,n,k,g,h;
for(j=1;j<=8;j++)
{max=a[j][j];
for(k=j+1;k<=9;k++)
{if(fabs(a[k][j])>fabs(max))max=a[k][j];}
for(k=j;k<=9;k++)
{if(a[k][j]/max==1)g=k;} /*确定本列绝对值最大元素所在行:g行*/
for(h=j;h<=10;h++)
y[h]=a[j][h];
for(h=j;h<=10;h++)
a[j][h]=a[g][h];
for(h=j;h<=10;h++)
a[g][h]=y[h]; /*将g行与J行所有元素进行交换*/
for(i=j+1;i<=9;i++)
for(j1=j+1;j1<=10;j1++)
a[i][j1]-=(a[i][j]/a[j][j])*a[j][j1];} /*逐行消元,将矩阵转化为上三角矩阵*/
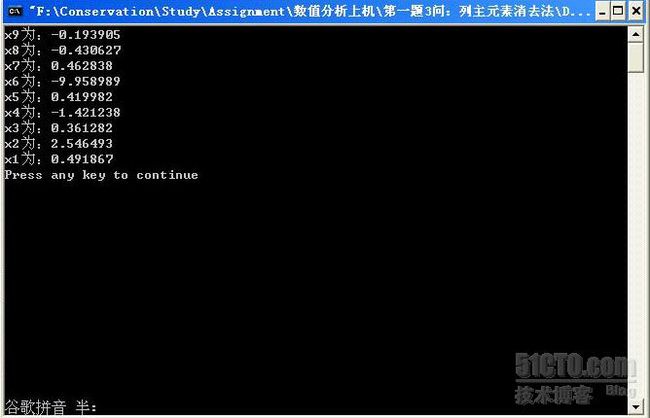
printf("x9为:%lf\n",x[9]=a[9][10]/a[9][9]);
for(m=8;m>=1;m--)
{sum=0;
for(n=m+1;n<=9;n++)
sum+=x[n]*a[m][n];
printf("x%d为:%lf\n",m,x[m]=(a[m][10]-sum)/a[m][m]);} /*从x9到x1逐个解出结果*/
}
3.计算结果
4.问题讨论(误差分析、上机出现情况等)
(1)这道题目出现的最大问题在 for(j1=j+1;j1<=10;j1++)a[i][j1]-=(a[i][j]/a[j][j])*a[j][j1]; ,刚开始我错写为:for(j1=j;j1<=10;j1++)a[i][j1]-=(a[i][j]/a[j][j])*a[j][j1]; ,也就是j1应该从j+1开始取值,如果从j开始取,会导致a[i][j1]-=(a[i][j]/a[j][j])*a[j][j1]; 一句中a[i][j]是零,这样后面的a[i][j1]全部都将是原来的数值,不会变化,导致错误。
(2)对于列主元素消元法,个人感觉将a,b两个矩阵,放在一个矩阵中进行编程,较方便。
第三题:三次样条插值求近似值
1.解题理论依据或方法应用条件:
依据三弯矩插值法列出相应的方程,然后将x的值带入(在求解三弯矩方程的参数时,应用追赶法求解方程组求出相应参数值)。
2.计算程序(使用软件:VC):
#include
#include
main()
{ int i;
double s,z; /*定义函数近似值,导数近似值*/
double b[11]={0,2,2,2,2,2,2,2,2,2,2},p[11],g[11],l[11]; /*追赶法中变量b,β,δ,l*/
double m[11]={0,0,0,0,0,0,0,0,0,0,0};
doublef[11]={0,0,0.69314718,1.0986123,1.3862944,1.6094378,1.7917595,1.9459101,2.079445,2.1972246,2.3025851}; /*原插值点对应函数值*/
double y[11]={0,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5,1}; /*变量η*/
double x[10]={0,1,0.5,0.5,0.5,0.5,0.5,0.5,0.5,0.5}; /*变量λ*/
doubled[11]={0,6*(f[2]-1),3*(f[3]+f[1]-2*f[2]),3*(f[4]+f[2]-2*f[3]),3*(f[5]+f[3]-2*f[4]),3*(f[6]+f[4]-2*f[5]),3*(f[7]+f[5]-2*f[6]),3*(f[8]+f[6]-2*f[7]),3*(f[9]+f[7]-2*f[8]),3*(f[10]+f[8]-2*f[9]),6*(0.1-f[10]+f[9])};
p[1]=2;g[1]=d[1];
for(i=1;i<=9;i++)
{l[i+1]=y[i]/p[i];
p[i+1]=b[i+1]-l[i+1]*x[i];
g[i+1]=d[i+1]-l[i+1]*g[i];} /*求出追赶法中相应参数*/
m[10]=g[10]/p[10];
for(i=9;i>=1;i--)
m[i]=(g[i]-x[i]*m[i+1])/p[i]; /*应用追赶法求出最终方程解*/
s=m[4]*pow(5-4.563,3)/6+m[5]*pow(4.563-4,3)/6+(f[4]-m[4]/6)*(5-4.563)+(f[5]-m[5]/6)*(4.563-4);
z=-m[4]/2*pow(5-4.563,2)+m[5]/2*pow(4.563-4,2)-(f[4]-m[4]/6)+(f[5]-m[5]/6);
printf("函数f(4.563)近似值 :%.16lf\n导数f'(4.563)近似值:%.16lf\n",s,z);
/*求出函数值和导数值并输出*/}
3.计算结果
4.问题讨论(误差分析、上机出现情况等)
(1)在做数组相关的编程时,特别注意下标的使用,因为数组下标是从0开始的,以后可以统一将下标为0的数组位置置0,从下标为1的位置开始赋值使用。
(2)编程的过程出现问题如下:①第二个for循环i--误写成i++,造成无限循环错误②在乘法的运算中漏掉了两个小括号间的“×”号