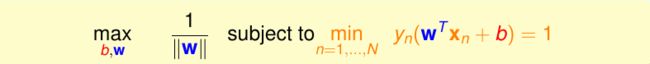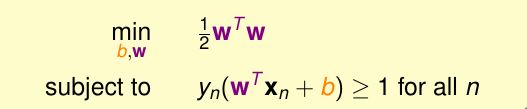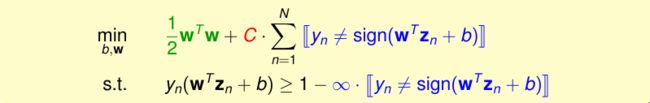1、SVM简介
给定训练样本集D,分类学习最基本的想法就是基于D在样本空间中找到一个超平面,将不同种类的样本分开。但能将训练样本分开的超平面有很多,比如PLA(Perceptron Linear Algorithm,即线性感知机算法)的运行结果就会随着初始化的不同而发生变化,在众多选择当中,哪个超平面最好呢?
以上三个超平面中直观来看应该是第三个超平面最好,因为前两个超平面都有距离其很近的点,但第三个超平面距离各个样本点都比较远。为什么距离样本点远就“好”呢?这是因为样本是含有随机扰动的,而距离样本点远意味着该超平面对训练样本的局部扰动容忍性最好。
既然距离各样本点越远的边界越好,我们就可以试着寻找最佳的超平面,即与最近样本点的距离最大的超平面。从而问题就转化为一个优化问题。如下图所示:
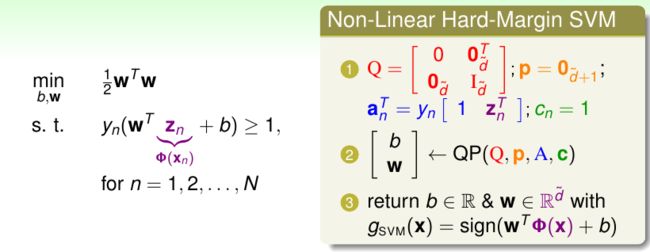
假定超平面的参数方程为,那么上述问题的规划形式如下:
这个规划如何求解呢?首先我们可以通过一些变形操作来简化其形式,我们知道超平面和超平面实际上表示的是一个平面,也就是说,系数同比例放缩并不影响结果,因此我们调整和使得,这样做的好处一是可以去掉规划中的min,二是这个条件包含了的条件,此时规划可以写成:
可以看到规划的形式已经简单了很多。进一步简化得到:
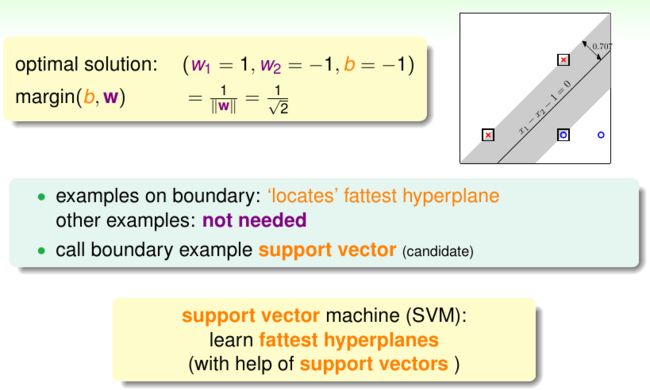
在求解这个规划之前,我们先来看一下这个规划和SVM的关系,或者说SVM这个名称的由来。假设我们已经由上面的规划解出了最优解平面:
从图中可以看出,样本点可以分为两类,一类是位于boundary上的,另一类则是不在boundary上的,不难看出,我们的boundary仅由位于boundary上的这部分样本点决定,因为这些点微微变化一下位置将可能导致boundary发生变化,而boundary外的点微微变化一下位置并不会对boundary产生影响。因此,直观看来是位于boundary上的样本“支撑”起了整个boundary,这部分样本点我们称之为支持向量,而借助支持向量寻找最优超平面的算法就称为支持向量机(SVM)。
至于求解规划的具体步骤,这里不做详细说明(超纲了……),我们只需要知道这个规划是一个二次规划问题,有现成的QPSolver可以使用。
说了这么多,我们一直默认距离样本点远的超平面更好,这是一种直观的感觉,有没有更好的解释呢?实际上,我们可以把SVM当成一种特殊的正则化:
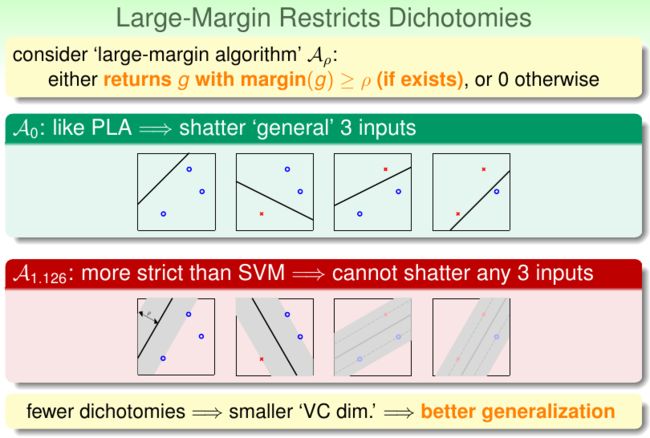
当然,我们也可以从VC维的角度来理解:
当我们考虑大margin的算法时,由于限制变强,可能导致break point变小,也就是VC维变小,这样一来意味着模型将拥有更好的泛化性能。这恰好和正则化的目标一致。
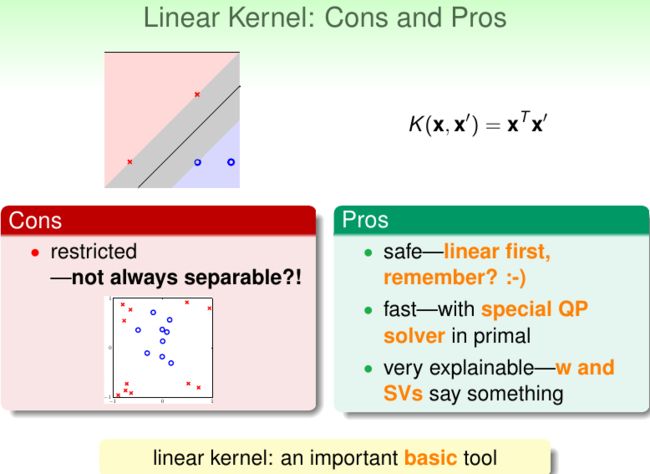
以上就是线性SVM,推广到非线性SVM也很简单,使用x的非线性函数去替代x即可:
2、Dual SVM
上面我们略过了SVM求解的具体细节,但我们需要了解求解SVM的复杂程度。上图表明了QP求解输入的参数,我们看到,样本特征的维数会影响矩阵的维度,进而直接影响求解的复杂度,当特征维数很大时,我们如何能较快地求解SVM呢?
原规划中,维数体现为个变量,而样本数量体现为个约束,即N个点到平面距离的约束。由运筹学的知识知,我们可以将一个规划表示为其对偶规划,从而使得变量和约束的个数互换。这是解决SVM求解复杂度高的一个很好的思路。(这里回顾对偶规划的相关内容并记录于https://www.jianshu.com/p/14ee7e8f14d6)
下面我们对原规划做变换,第一步我们先用拉格朗日乘子法去掉约束:
然后我们得出拉格朗日对偶问题:
这个形式其实就是运筹学中的弱对偶定理,其表述为原问题是极小化问题时,原问题任意可行的目标函数值是其对偶问题目标函数值的上界;反之对偶问题任一可行解的目标函数值是其原问题目标函数的下界。
那么这个问题是否满足强对偶定理呢?所谓强对偶定理,就是若原始问题(对偶问题)有一个确定的最优解,那么对偶问题(原始问题)也有一个确定的最优解,而且这两个最优解所对应的目标函数值相等。
对于二次规划,强对偶性需要满足以下条件:
接下来我们求解右边的拉格朗日对偶,首先,我们可以看到括号内关于的优化问题是无约束的,因此直接求导即可简化问题:
由此,我们可以写出KKT条件。在优化理论中,KKT条件是非线性规划(nonlinear programming)最优解的必要条件。
至此,我们可以写出Dual SVM的规划如下:
我们看到,原始规划中的变量数目已经变成样本数了。当然,对偶问题解出的并非我们需要的,而是拉格朗日系数,下一步我们可以由互补松弛定理来确定:
这里需要注意,我们只需要找到某一个即可由求得。
另外,则,意味着样本点在boundary上,即此样本是一个支持向量(SV)。
至此我们可以看到,只由大于零的确定,也是由大于零的确定,即超平面完全由支持向量(SV)确定。这也暗示了SVM的复杂度主要与SV的数目有关。
现在我们回顾一下上面做的事情,是否达到了我们的目标呢?我们是否真正简化了SVM的求解过程,使其不再依赖变量的维数呢?其实还没有真正做到这一点:
3、Kernel SVM
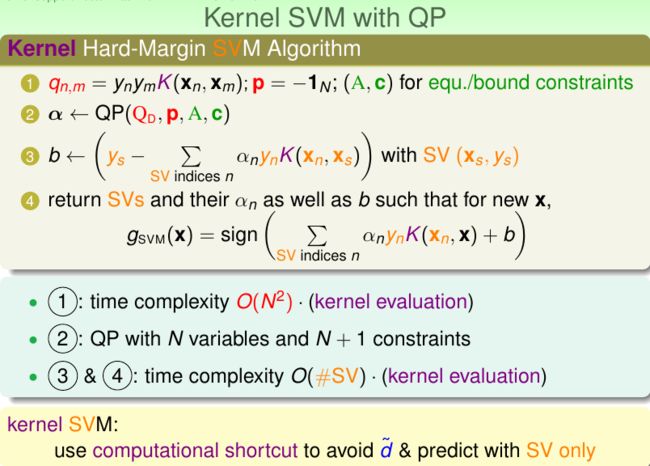
上面我们讨论了Dual SVM并将原来的模型做了简化,简化后使用QPSolver求解N不太大的SVM效率已经得到提升,但上图显示了我们的计算过程实际上依然依赖于。这一节我们希望使用核函数来解决这个问题。
我们先通过面临的问题来引出核函数:
我们看到,现在需要解决的核心问题是原特征向量经过特征映射后得到的更加复杂的特征向量之间的内积计算。举个例子,假如表示二次多项式特征映射:
通过数学上的运算技巧我们把两个维向量的内积运算的复杂度由()优化到了。这是非常神奇的!
按原来的计算方法,我们需要先由维的原特征向量计算映射后的维的特征向量,然后对的向量做内积。而核函数可以帮助我们把这两个步骤合二为一:
可以看到,借助高效的核函数,我们成功地摆脱了求解SVM过程中对的依赖,大大提升了算法的效率。
其具体的时间复杂度简要分析如下:
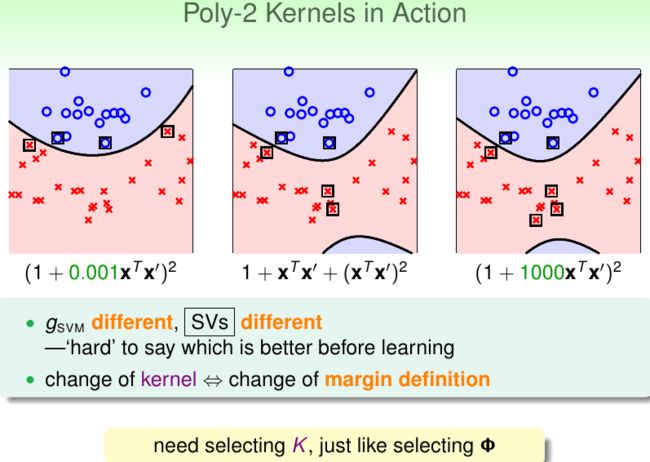
既然核函数这么好用,那么很自然的一个问题就是,我们如何选取核函数呢?其实这和如何选取特征映射是同一个问题。拿二次多项式特征映射来说,就有很多种形式:
不同的核函数会产生不同的超平面,对应的支持向量(SV)也可能不同:
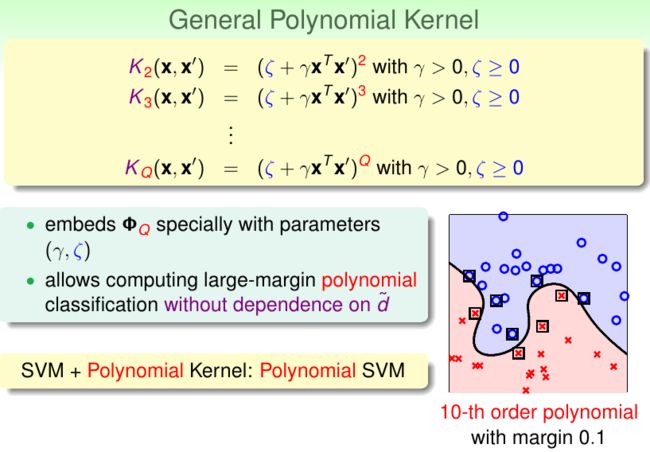
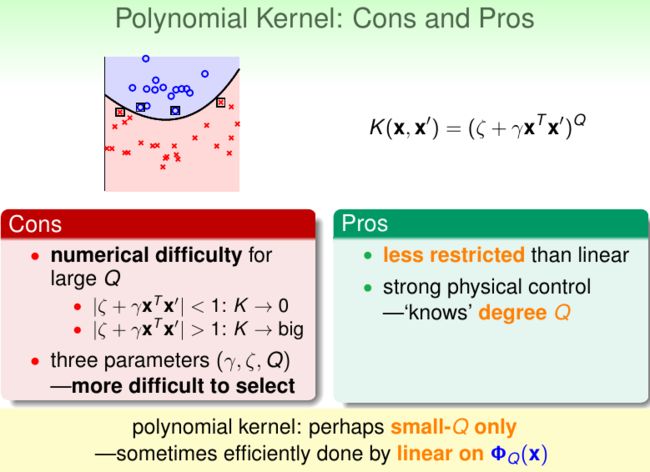
上面我们讨论了二次多项式特征映射,更为一般的,我们还可以使用各次多项式特征映射得到更为复杂的边界,而且随着模型最高次数的增长,计算代价并不会增加太多。这使得我们可以较快地训练出较复杂的模型。
既然我们现在的SVM求解过程不再依赖于,那么我们是否可以处理无限维的特征呢?答案是肯定的!我们的核函数依然可以高效地完成计算。
高斯核函数是最常用的径向基函数(RBF),形式为:
其中为核函数中心,σ为函数的宽度参数 ,控制了函数的径向作用范围。
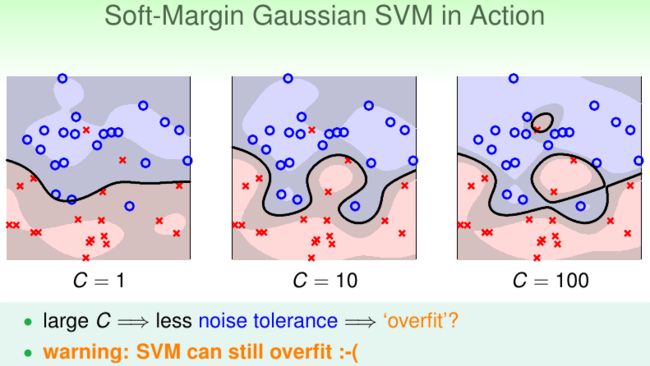
高斯核函数很强大,但参数选取要小心,很容易导致过拟合:
最后我们看一下常用核函数的优缺点及比较:
4、Soft-Margin SVM
上面我们已经展示了Kernel SVM容易导致过拟合,接下来我们要解决过拟合问题。
从上图中我们可以看到,当训练样本中包含噪声点的时候,如果用较复杂的核函数且坚持要把所有点分类正确(这就是Hard-Margin SVM所要求的),那么模型就会拟合噪声点,从而发生过拟合。
这里有两个解决方案,一是选择合适的核函数,这是比较难做到的;二是放宽要求,只要求大部分样本点分类正确,允许一小部分样本点突破margin的限制,甚至分类错误。
由上图可以看到,我们采用添加正则项的方式来放宽要求,在大的margin和对噪声的容忍度之间做了trade-off。这样我们就得到了Soft-Margin版本的SVM:
现在问题来了,指示函数并不是线性的,也不是连续的,这个规划不再是QP了,因此求解变得很复杂,看来我们的正则项直接用错误分类的样本个数并不是一个好的选择。如何修改呢?一个简单的思路就是考查错分的样本偏离boundary的距离,距离越大,罚项就越大:
接下来,为了求解这个Soft-Margin SVM,我们需要进行和之前类似的操作。首先求原规划的拉格朗日对偶:
经过一些列和之前相似的操作,我们得到标准的Soft-Margin SVM对偶规划:
可以看到,和Hard-Margin SVM相比,Soft-Margin SVM不一样的就只有多了一个上界的限制。
进一步的,我们也可以将核函数的技巧应用于Soft-Margin SVM得到Kernel Soft-Margin SVM:
我们依然是先通过对偶规划解得,进而解出,从而得到原规划的解。这里唯一的问题是的求解所运用的互补松弛条件和之前不同:
此时只能说明对应的是SV,但这个SV有可能在boundary上也可能是违反了margin限制的样本点,我们需要把这部分样本筛出去,用的就是这个条件,当成立时,对应的,即没有违反margin限制,从而说明其是boundary上的SV。这部分SV称为free SV。
和Hard-Margin SVM类似,这里我们只需要free SV就可以构建出模型的解了。
我们看一下不同的的取值对应的样本点的性质:
当然,Kernel Soft-Margin SVM依然是可能过拟合的,不过我们可以调节C来缓解这一情况,C的选取可以借助验证集(因为C是超参)。
最后,让我们用正则化的视角来看待Soft-Margin SVM,还记得我们选取的代表什么吗,代表的是第n个样本突破Margin限制的距离,于是我们可以把之前的规划写成无约束形式:
这个形式为什么看起来这么眼熟呢?观察最右边一项可以发现,这不就是hinge loss嘛!(),这样看来,我们之前一直看作正则项的部分其实可以看成损失,而把另一部分看作正则项:
这样的视角转换十分有趣,因为使用正则项的方法很多,现在我们可以很方便的把Soft-Margin和其它的模型进行比较,还有一个重要意义在于,以前我们把看作loss的时候loss是固定的形式,现在我们可以选择loss的形式了,除了hinge,也可以选择对率损失、指数损失等。
由上表可以看到,固定正则项,当要求loss为0的时候,我们有Hard-Margin SVM,当选择loss为hinge loss的时候,我们得到Soft-Margin SVM。那么loss取logistic loss()呢?
如果loss取logistic loss,就得到logistic regression模型。我们可以看到,hinge loss和logistic loss均为0/1 loss的upper bound且二者相差并不大,这就意味着Soft-Margin SVM和Logistic Regression的目标是非常相近的。实际上,通常两者性能也相当。LR的优势主要在于其输出有自然的概率意义,SVM则不具备这个特点;此外,LR可直接用于多分类任务,SVM则需要特殊处理。SVM的优势在于hinge loss有平坦的零区域,这使得SVM的解具有稀疏性,而LR不能导出类似的SV概念,其解依赖于更多样本,开销较大。
更为一般的情况西瓜书上做了如下总结:
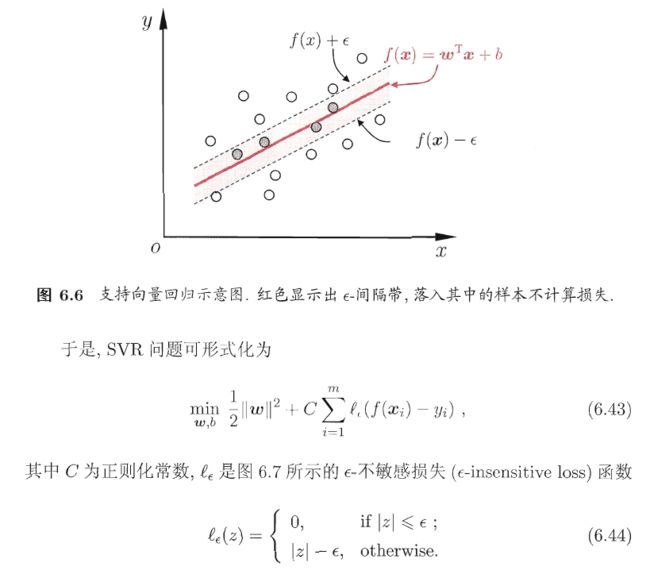
5、SVR(支持向量回归)
SVR与SVM的思想类似,都是要设置Margin,只不过SVM是在Margin外的样本点不计算损失,违反了Margin的样本点计算损失,而SVR恰好相反,在Margin内的样本不计算损失,在Margin外的样本才计算损失:
和最小二乘回归的平方误差的对比如下:
下面我们列出SVR的规划,注意这里的间隔带两侧的松弛程度可以有所不同,因此这里设置两个松弛变量:
然后与SVM类似的,求拉格朗日对偶,然后利用互补松弛定理求解模型:
不难看出,由互补松弛定理的得到:对于在tube内的样本点来说,,因此对应样本点对没有影响。对于在tube上或tube外的点,,因此对有影响。
因此和SVM类似,SVR的解也具有稀疏性。
6、核方法
关于核方法,最重要的就是表示定理,西瓜书上这部分的推导有些复杂了,林轩田老师Slides上的一个表示定理的特殊情形其实已经可以覆盖很多模型了:
其实表示定理证明的就是模型最优解可以用的线性组合表示出来,这对于核函数发挥作用意义重大,因为只有,模型计算的结果才能表示成核函数的线性组合,从而避免直接进行和之间的内积运算,而是直接通过原空间中两个点()的内积算得新空间中对应的两个点()之间的内积。: