流形学习
低维流形空间映射到高维空间中去(低维 -> 高维,看了一天觉得这样好理解),也就是说一个高维空间可以有一个简单的低维流形空间来刻画。
- 举个简单的栗子,一个圆在二维空间中需要(x,y)两个坐标参数,而在极坐标系中只需要半径r一个参数就可以刻画出来了,也就是说高维空间中存在性质的冗余。流形学习要做的就是找到高维空间的嵌入空间(低维空间,嵌入空间是给后面的sklearn埋下伏笔
网上冲浪的许久,这个回答(麋路)让我赞了
t-SNE技术
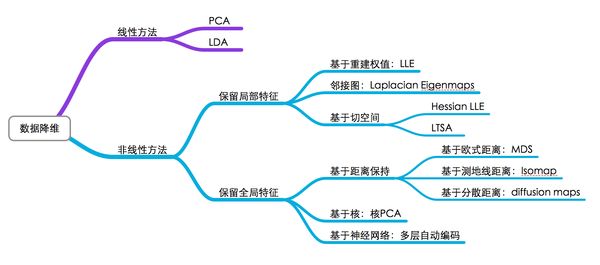
机器学习中降维的技术有很多种,上图是一些常见的降维技术,而SNE和t-SNE是才出现不久的降维技术,两者的差别不大主要是低维空间中概率函数选择的不同,因为t-SNE好很多,所以果断选择后者++
引入简介
在人们的常识中,物件之间越接近则有很大可能是属于同一类。而在线性降维的过程中确实是这样子体现的,但是如果是复杂的高维空间(下图),两点之间是否接近就不能用简单的欧氏距离来衡量了,数据之间的内在特征就无法表达出来。

举个栗子:在50维空间中有11个点它们之间的距离两两相等,而如果在二维空间中能表示几个点之间的距离两两相等的最多只有三个,这就告诉了我们这样子描述数据之间的相似程度是行不通的。
t-SNE技术采用新的概率分布衡量方式保证在高低维空间中内在特征不被破坏,同时保证较好的区分能力- 衡量距离的新方法-相似程度
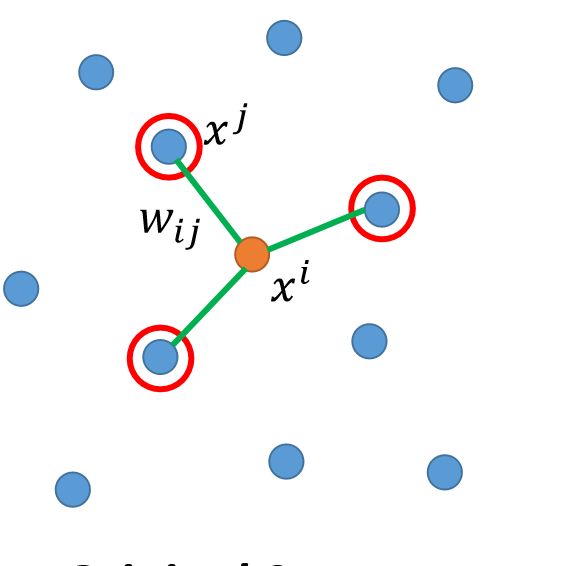
在t-SNE技术中高维空间中的点\(x^i,x^j\)服从高斯分布\(f(x)=\frac{1}{\sqrt{2\pi \sigma}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\),降低后的低维空间中的点\(z^i,z^j\)服从t分布
| \ | 高维空间 | 低维空间 |
|---|---|---|
| \(x^i,x^j\)之间的距离 | \(S(x^i,x^j)=\frac{1}{\sqrt{2\pi \sigma}}e^{-\frac{(x^i-x^j)^2}{2\sigma^2}}\) | \ |
| \(z^i,z^j\)之间的距离 | \ | \(S'(z^i,z^j)=\frac{1}{(z^i-z^j)^2}\) |
| 任意两点间的相似程度: | \(P(x^j|x^i)=\frac{S(x^j,x^i)}{\sum_{k\neq i}S(x^j,x^k)}\) | \(P'(z^j|z^i)=\frac{S'(z^j,z^i)}{\sum_{k\neq i}S(z^j,z^k)}\) |
理想状态下数据的性质是不会改变的,只是表现方式改变而已,也就是说在不同维度下对应的任意相同两点间的相似程度应该相等,即在整个相似程度方程上来看,\(P(x^i,x^j)\)与\(P'(z^i,z^j)\)是完全相同的分布,这就找到了我们需要优化的对象。
| \ | 描述 |
|---|---|
| 优化目的 | \(P(x^i,x^j)\)与\(P'(z^i,z^j)\)尽可能的相似 |
| 优化对象 | KL散度方程\(C=\sum_iKL(P_i||P'_i)=\sum_i\sum_jP_{j|i}log\frac{P_{j|i}}{P'_{j|i}}\) |
| 优化方法 | 梯度下降(晕),通过GD找到最优的一组\(z^i\)参数即找到了低维空间 |
- 练习 sklearn
源码网络上都有,这里做一个简单的sklearn运用。t-SNE技术主要是用来数据可视化的,降至过低维数据的损失还是有的,还有很重要的一点是具体实现似乎是一遍聚类一遍降维来着(忘了),复杂度很高,需要的时间很多。
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import manifold, datasets
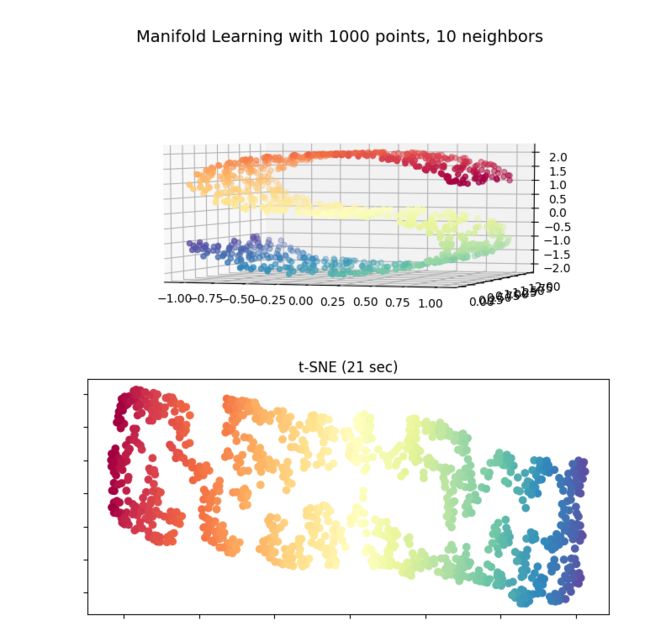
n_points = 1000
# X 是一个(1000, 3)的 2 维数据,color 是一个(1000,)的 1 维数据
X, color = datasets.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2
fig = plt.figure(figsize=(8, 8))
# 创建了一个 figure,标题为"Manifold Learning with 1000 points, 10 neighbors"
plt.suptitle("Manifold Learning with %i points, %i neighbors"
% (1000, n_neighbors), fontsize=14)
'''绘制 S 曲线的 3D 图像'''
ax = fig.add_subplot(211, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
ax.view_init(4, -72) # 初始化视角
'''t-SNE'''
t0 = time()
tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
Y = tsne.fit_transform(X) # 转换后的输出
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0)) # 算法用时
ax = fig.add_subplot(2, 1, 2)
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
plt.xticks([])
plt.yticks([])
plt.show()其实这个包有很多参数,比如困惑度(晕)和一些梯度下降需要用到的参数,这个贴出大佬传送门