Description of the Problem
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given [10, 9, 2, 5, 3, 7, 101, 18],
The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.
Follow up: Could you improve it to O(n log n) time complexity?
A rough idea
Begin from the first one, traverse the array.
keep track of the biggest and the next-to-biggest value
for each entry, do
if (nums[i] > Biggest) {
result++;
NextToBiggest = Biggest;
Biggest = nums[i];
} else if (nums[i] < Biggest && nums[i] > NextToBiggest) {
Biggest = nums[i];
} else if (NextToBiggest == Biggest) {
NextToBiggest = nums[i];
Biggest = nums[i];
}
the idea is to find the ascending subsequence while making sure the biggest value in this subsequence is as small as possible (To largen the range of selection)
class Solution {
public:
int lengthOfLIS(vector& nums) {
if (nums.size() == 0)
return 0;
int Biggest = nums[0], NextToBiggest = nums[0];
int result = 1;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > Biggest) {
result++;
NextToBiggest = Biggest;
Biggest = nums[i];
} else if (nums[i] < Biggest && nums[i] > NextToBiggest) {
Biggest = nums[i];
} else if (NextToBiggest == Biggest) {
NextToBiggest = nums[i];
Biggest = nums[i];
}
}
return result;
}
};
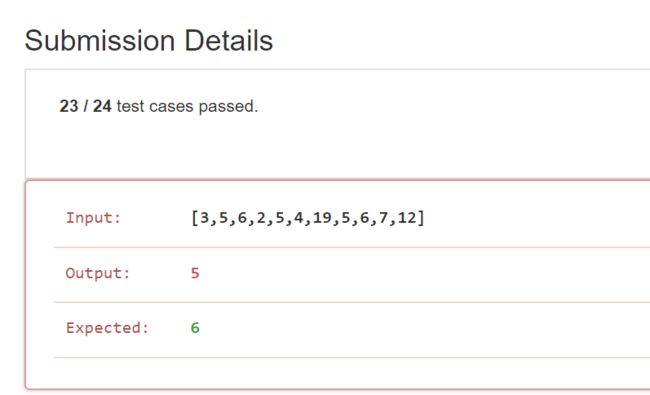
Sadly, this solution is almost correct
As is shown, the program can't find the longest subsequence of
2 4 5 6 7 12, whose size is 6.
All it could find is 3 5 6 7 12, whose size is 5.
We can see that when traversing to index 3, it has a sequence of 3 5 6 already and it's just not clever enough to abandon this sequence (for it's not the longest) with a new one beginning from index 3.
So an easy correction can be made :
Correction
We now traverse the array beginning from all the index, to see how large an increasing subsequence we can get and record the largest one.
class Solution {
public:
int lengthOfLIS(vector& nums) {
if (nums.size() == 0)
return 0;
int BiggestResult = 1;
for (int i = 0; i < nums.size() - 1; i++) {
int Biggest = nums[i], NextToBiggest = nums[i];
int result = 1;
for (int j = i + 1; j < nums.size(); j++) {
if (nums[j] > Biggest) {
result++;
NextToBiggest = Biggest;
Biggest = nums[j];
} else if (nums[j] < Biggest && nums[j] > NextToBiggest) {
Biggest = nums[j];
} else if (NextToBiggest == Biggest) {
NextToBiggest = nums[j];
Biggest = nums[j];
}
}
BiggestResult = result > BiggestResult ? result : BiggestResult;
}
return BiggestResult;
}
};
Not the best solution but at least it's an correct one.
On second thoughts, it might not even be correct.
DP Solution
Note that LIS[i] is the LIS at index[i].
for example LIS[0] = arr[0] = {3}.
LIS[1] = {3,5}.
Our goal is to find LIS[n]
Traverse the array, for each element of index i, we traverse from 0 to i-1, to find the biggest value smaller than arr[i].
For example, index 6, we traverse from 0~5, the biggest value smaller than 19 is 6 at index 2, and LIS[2] = {3,5,6} of length 3, so, the LIS at index 6 consists of LIS[2]+arr[6] = {3,5,6,19} of length 4.
That is, LIS[k] = MaxLIS(0~k-1) + arr[k].
class Solution {
public:
int lengthOfLIS(vector& nums) {
int *LIS, n = nums.size();
LIS = (int*) malloc ( sizeof( int ) * n );
/* Initialize LIS values for all indexes */
for (int i = 0; i < n; i++ )
LIS[i] = 1;
for (int i = 1; i < nums.size(); i++) {
int max = 0; // the max LIS between 0 ~ i-1 and that nums[i] > nums[j]
for (int j = 0; j <= i - 1; j++) {
if (nums[i] > nums[j] && LIS[j] > max) {
LIS[i] = LIS[j] + 1;
max = LIS[j];
}
}
if (max == 0) // can't find a j such that nums[i] > nums[j]
LIS[i] = 1;
}
int result = 0;
for (int i = 0 ; i < n ; i++) {
if (LIS[i] > result)
result = LIS[i];
}
return result;
}
};
Still the complexity is O(n*n) like the above one, not ideal enough.
An O(nlogn) solution
Why is this a RUNTIME ERROR?
class Solution {
public:
int lengthOfLIS(vector& nums) {
vector LIS;
LIS.resize(nums.size(), 1);
for (int i = 1; i < nums.size(); i++) {
int max = 0; // the max LIS between 0 ~ i-1 and that nums[i] > nums[j]
for (int j = 0; j <= i - 1; j++) {
if (nums[i] > nums[j] && LIS[j] > max) {
LIS[i] = LIS[j] + 1;
max = LIS[j];
}
}
if (max == 0) // can't find a j such that nums[i] > nums[j]
LIS[i] = 1;
}
return LIS.back();
}
};