sptv

多元高斯分布完全解析

摘要

高斯分布被誉为"上帝的分布", 其强悍的建模能力和优美的数学性质使得高斯分布在现实中得到广泛的应用. 由中心极限定理我们知道, 大量独立同分布的随机变量的均值在做适当标准化之后会依分布收敛于高斯分布, 这使得高斯分布具有普适性的建模能力. 数学上, 当使用高斯分布对贝叶斯推断的似然和先验进行建模时, 得到的后验同样为高斯分布, 即其具有共轭先验性质. 在随机过程理论中, 多元高斯分布则是高斯过程的理论基础. 这种种场景使得高斯分布颇受重视, 并发展出一套成熟完整的理论体系. 本文主要介绍多元高斯分布的由来与其背后的几何原理, 分为如下章节:

阐述多元标准高斯分布;
由多元标准高斯分布导出多元高斯分布;
阐述多元高斯分布的几何意义;
总结.

关键词: 多元高斯分布, 高斯过程, 概率论与数理统计, 机器学习

多元标准高斯分布

熟悉一元高斯分布的同学都知道, 若随机变量 , 则有如下的概率密度函数

而如果我们对随机变量进行标准化, 用对(1)进行换元, 继而有

$\begin{align} \because x(z) & = z \cdot \sigma + \mu \\ \therefore p(x(z)) & = \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^{-\frac{1}{2} \cdot (z)^2} \\ 1 & = \int_{-\infty}^{+\infty}{p(x(z))dx} \\ & = \int_{-\infty}^{+\infty}{ \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^{-\frac{1}{2} \cdot (z)^2}dx} \\ & = \int_{-\infty}^{+\infty}{ \frac{1}{\sqrt{2 \pi}} \cdot e^{-\frac{1}{2} \cdot (z)^2} dz} \tag{3} \end{align}$

此时我们说随机变量服从一元标准高斯分布, 其均值 , 方差 , 其概率密度函数为

需要注意的是, 为了保证概率密度函数在上的积分为1, 换元时需要求 , 从而得到(3).

随机变量标准化的过程, 实际上的消除量纲影响和分布差异的过程. 通过将随机变量的值减去其均值再除以标准差, 使得随机变量与其均值的差距可以用若干个标准差来衡量, 从而实现了不同随机变量与其对应均值的差距, 可以以一种相对的距离来进行比较.

一元标准高斯分布与我们讨论多元标准高斯分布有什么关系呢? 事实上, 多元标准高斯分布的概率密度函数正是从(4)导出的. 假设我们有随机向量 , 其中且彼此独立, 即随机向量中的每个随机变量都服从标准高斯分布且两两彼此独立. 则由(4)与独立随机变量概率密度函数之间的关系, 我们可得随机向量的联合概率密度函数为

$\begin{align} p(z_1, \cdots, z_n) & = \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi}} \cdot e^{-\frac{1}{2} \cdot (z_i)^2} \\ & = \frac{1}{(2 \pi)^{\frac{n}{2}}} \cdot e^{-\frac{1}{2} \cdot (Z^\top Z)} \\ 1 & = \int_{-\infty}^{+\infty} \cdots \int_{-\infty}^{+\infty} p(z_1, \cdots, z_n) \ dz_1 \cdots dz_n \tag5 \end{align}$

我们称随机向量 , 即随机向量服从均值为零向量, 协方差矩阵为单位矩阵的高斯分布. 在这里, 随机向量的协方差矩阵是组成的矩阵, 即

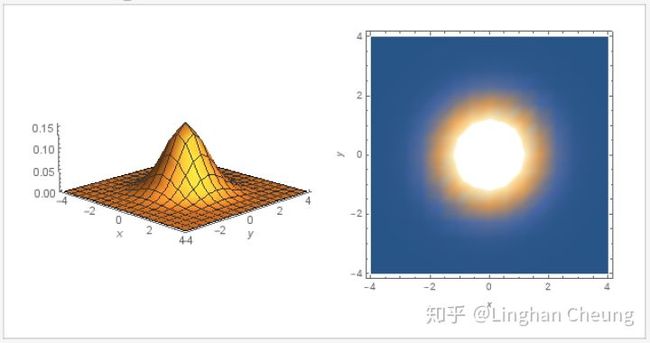
由于随机向量 , 所以其协方差矩阵的对角线元素为1, 其余元素为0. 如果我们取常数 , 则可得函数的等高线为 , 当随机向量为二维向量时, 我们有

由(7)我们可知, 其等高线为以(0, 0)为圆心的同心圆.

二元标准高斯分布概率密度函数图

多元高斯分布

由上一节我们知道, 当随机向量时, 其每个随机变量彼此独立, 我们可通过(4)与独立随机变量概率密度函数之间的关系得出其联合概率密度函数(5). 那对于普通的随机向量 , 即其每个随机变量且彼此不独立的情况下, 我们该如何求随机向量的联合概率密度函数呢? 一个很自然的想法是, 如果我们能通过线性变换, 使得随机向量中的每个随机变量彼此独立, 则我们也可以通过独立随机变量概率密度函数之间的关系求出其联合概率密度函数. 事实上, 我们有如下定理可完成这个工作

定理1: 若存在随机向量 , 其中为均值向量, 半正定实对称矩阵为的协方差矩阵, 则存在满秩矩阵 , 使得 , 而 .

有了定理1, 我们就可以对随机向量做相应的线性变换, 使其随机变量在线性变换后彼此独立, 从而求出其联合概率密度函数, 具体地

$\begin{align} & \because & \vec{Z} & = B^{-1}(\vec{X} - \vec{\mu}), \vec{Z} \sim \mathcal{N}(\vec{0}, I) \tag8 \\ & \therefore & p(z_1, \cdots, z_n) & = \frac{1}{(2 \pi)^{\frac{n}{2}}} \cdot e^{-\frac{1}{2} \cdot (Z^\top Z)} \\ & & p(z_1(x_1, \cdots, x_n), \cdots) & = \frac{1}{(2 \pi)^{\frac{n}{2}}} \cdot e^{-\frac{1}{2} \cdot [(B^{-1}(\vec{X} - \vec{\mu}))^\top (B^{-1}(\vec{X} - \vec{\mu}))]} \\ & & & = \frac{1}{(2 \pi)^{\frac{n}{2}}} \cdot e^{-\frac{1}{2} \cdot [(\vec{X} - \vec{\mu})^\top (BB^\top)^{-1}(\vec{X} - \vec{\mu})]} \\ & \therefore & 1 = \int_{-\infty}^{+\infty} & \cdots \int_{-\infty}^{+\infty} p(z_1(x_1, \cdots, x_n), \cdots) \ dz_1 \cdots dz_n \\ & & = \int_{-\infty}^{+\infty} & \cdots \int_{-\infty}^{+\infty} \frac{1}{(2 \pi)^{\frac{n}{2}}} \cdot e^{-\frac{1}{2} \cdot [(\vec{X} - \vec{\mu})^\top (BB^\top)^{-1}(\vec{X} - \vec{\mu})]} \ dz_1 \cdots dz_n \tag9 \end{align}$

由多元函数换元变换公式, 我们还需要求出雅可比行列式 , 由(8)可得

由(9)(10), 我们可进一步得

$1 = \int_{-\infty}^{+\infty} \cdots \int_{-\infty}^{+\infty} \frac{1}{(2 \pi)^{\frac{n}{2}} \left| B B^\top \right|^{\frac{1}{2}}} \cdot e^{-\frac{1}{2} \cdot [(\vec{X} - \vec{\mu})^\top (BB^\top)^{-1}(\vec{X} - \vec{\mu})]} \ dx_1 \cdots dx_n \tag{11}$

我们得到随机向量的联合概率密度函数为

在(12)中, 随机向量的协方差矩阵还未得到体现, 我们可通过线性变换(8)做进一步处理

$\begin{align} \Sigma & = \mathbf{E}[(\vec{X} - \vec{\mu})(\vec{X} - \vec{\mu})^\top] \\ & = \mathbf{E}[(B\vec{Z} - \vec{0})(B\vec{Z} - \vec{0})^\top] \\ & = \mathbf{Conv}(B\vec{Z}, B\vec{Z}) \\ & = B \mathbf{Conv}(\vec{Z}, \vec{Z}) B^\top \\ & = BB^\top \tag{13} \end{align}$

我们发现, (12)中就是线性变换前的随机向量的协方差矩阵 , 所以由(12)(13), 我们可以得到联合概率密度函数的最终形式

原本由定理1, 我们还需要求线性变换矩阵 , 才能确定随机向量的联合概率密度函数的表达式, 现在由(13)我们即可得最终形式(14), 随机向量的联合概率密度函数由其均值向量和其协方差矩阵唯一确定, 但我们需要明白的是, 这是通过定理1的线性变换得到的, 即此线性变换隐含其中.

如果我们取常数 , 则可得函数的等高线为 , 当随机向量为二维向量时, 我们对协方差矩阵进行分解, 因为其为实对称矩阵, 可正交对角化

$\begin{align} \Sigma & = Q \Lambda Q^\top \\ c' & = (\vec{X} - \vec{\mu})^\top (Q \Lambda Q^\top)^{-1}(\vec{X} - \vec{\mu}) \\ & = (\vec{X} - \vec{\mu})^\top Q \Lambda^{-1} Q^\top(\vec{X} - \vec{\mu}) \\ & = [Q^\top (\vec{X} - \vec{\mu})]^\top \Lambda^{-1} [Q^\top(\vec{X} - \vec{\mu})] \tag{15} \end{align}$

由于矩阵是酉矩阵, 所以可以理解为将随机向量 , 均值向量在矩阵的列向量所组成的单位正交基上进行投影并在该单位正交基上进行相减. 我们不妨记投影后的向量分别为 , 同时记矩阵 , 则(15)的二次型可表示为

由(16)我们可知, 此时函数的等高线是在矩阵的列向量所组成的单位正交基上的一个椭圆, 椭圆的中心是 , 长半轴为 , 短半轴为 .

如果协方差矩阵不是对角矩阵, 则正交对角化得到的酉矩阵不是标准正交基, 其代表一个旋转, 此时的椭圆应该是一个倾斜的椭圆, 随机向量中的随机变量不是彼此独立的;

倾斜椭圆-二元高斯分布概率密度函数图

如果协方差矩阵是对角矩阵, 则正交对角化得到的酉矩阵就是标准正交基, 则前述的投影是在标准正交基上完成的, 此时的椭圆应该是一个水平的椭圆, 随机向量中的随机变量就是彼此独立的.

水平椭圆-二元高斯分布概率密度函数图

多元高斯分布的几何意义

现在我们知道, 随机向量的联合概率密度函数是通过线性变换的帮助, 将随机向量的各个随机变量去相关性, 然后利用独立随机变量概率密度函数之间的关系得出的, 亦既是定理1所表述的内容. 那具体地, 线性变化是怎么去相关性使随机向量的各个随机变量彼此独立的呢? 我们不妨在二维平面上, 再次由定理1和(15)出发来看看这个去相关性的过程.

由定理1我们有

$\begin{align} & \because & \vec{Z} & = B^{-1}(\vec{X} - \vec{\mu}), \vec{Z} \sim \mathcal{N}(\vec{0}, I) \\ &\therefore & \vec{Z}^\top \vec{Z} & = (B^{-1}(\vec{X} - \vec{\mu}))^\top (B^{-1}(\vec{X} - \vec{\mu})) \\ & & & = (\vec{X} - \vec{\mu})^\top (BB^\top)^{-1}(\vec{X} - \vec{\mu}) \\ & & & = (\vec{X} - \vec{\mu})^\top \Sigma^{-1}(\vec{X} - \vec{\mu}) \tag{17} \end{align}$

再由(15)(17)可得

$\begin{align} \vec{Z}^\top \vec{Z} & = [Q^\top (\vec{X} - \vec{\mu})]^\top \Lambda^{-1} [Q^\top(\vec{X} - \vec{\mu})] \\ & = [Q^\top (\vec{X} - \vec{\mu})]^\top (\Lambda^{-\frac{1}{2}})^\top \Lambda^{-\frac{1}{2}} [Q^\top(\vec{X} - \vec{\mu})] \\ & = [\Lambda^{-\frac{1}{2}}Q^\top (\vec{X} - \vec{\mu})]^\top [\Lambda^{-\frac{1}{2}} Q^\top(\vec{X} - \vec{\mu})] \\ & = [(Q \Lambda^{-\frac{1}{2}})^\top (\vec{X} - \vec{\mu})]^\top [(Q \Lambda^{-\frac{1}{2}})^\top (\vec{X} - \vec{\mu})] \\ & = [(Q \cdot \begin{bmatrix} \frac{1}{\sqrt{\lambda_1}} & 0 \\ 0 & \frac{1}{\sqrt{\lambda_2}} \end{bmatrix})^\top (\vec{X} - \vec{\mu})]^\top \\ & \cdot \ \ [(Q \cdot \begin{bmatrix} \frac{1}{\sqrt{\lambda_1}} & 0 \\ 0 & \frac{1}{\sqrt{\lambda_2}} \end{bmatrix})^\top (\vec{X} - \vec{\mu})] \tag{18} \end{align}$

由(18)我们已经可以非常明显地看出线性变换的具体操作了

$\underbrace{(\underbrace{Q \cdot \underbrace{\begin{bmatrix} \frac{1}{\sqrt{\lambda_1}} & 0 \\ 0 & \frac{1}{\sqrt{\lambda_2}} \end{bmatrix}}_{对标准正交基拉伸}}_{对拉伸后的正交基旋转} )^\top (\vec{X} - \vec{\mu})}_{将随机向量\vec{X}去均值后在新正交基上投影} \tag{19}$

我们先对标准正交基进行拉伸, 横轴和纵轴分别拉伸倍, 再使用酉矩阵对拉伸后的正交基进行旋转, 最后将去均值的随机向量在新的正交基上进行投影, 从而使完成线性变换后的随机变量在新的正交基上彼此独立. 值得注意的是, 如果随机向量本来就是独立随机变量组成的, 此时其协方差矩阵是一个对角矩阵, 则酉矩阵是一个单位矩阵 , 此线性变换中只有拉伸而没有旋转.

多元高斯分布随机变量去相关性图

而如果我们只保留这个投影后坐标轴长度较长的对应的坐标, 我们就可以达到将随机向量进行降维的效果, 而这, 就是所谓的PCA(principal component analysis, 主成分分析).

总结

本文从多元标准高斯分布出发, 阐述了如何通过线性变换, 将任意的服从多元高斯分布的随机向量去相关性, 并求出其联合概率密度函数的过程, 最后给出了线性变换的具体过程阐述. 多元高斯分布是许多其他理论工具的基础, 掌握它是进行其他相关理论研究的关键.

引用

[1] Wikipedia contributors. "中心极限定理."维基百科, 自由的百科全书. 维基百科, 自由的百科全书, 9 May 2018. Web. 9 May 2018.‹https://zh.wikipedia.org/w/index.php?title=%E4%B8%AD%E5%BF%83%E6%9E%81%E9%99%90%E5%AE%9A%E7%90%86&oldid=49494817›.

[2] Do, C. (2008).The Multivariate Gaussian Distribution. [online] Cs229.stanford.edu. Available at: http://cs229.stanford.edu/section/gaussians.pdf [Accessed 13 Mar. 2019].

[3] 张, 伟. (2019). 多元正态分布. [online] Staff.ustc.edu.cn. Available at: http://staff.ustc.edu.cn/~zwp/teach/MVA/Lec4_slides.pdf [Accessed 13 Mar. 2019].

[4] Wikipedia contributors. "多元正态分布."维基百科, 自由的百科全书. 维基百科, 自由的百科全书, 16 Sep. 2018. Web. 16 Sep. 2018.‹https://zh.wikipedia.org/w/index.php?title=%E5%A4%9A%E5%85%83%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83&oldid=51304757›.

[5] Wikipedia contributors. "雅可比矩阵."维基百科, 自由的百科全书. 维基百科, 自由的百科全书, 7 Dec. 2018. Web. 7 Dec. 2018.‹https://zh.wikipedia.org/w/index.php?title=%E9%9B%85%E5%8F%AF%E6%AF%94%E7%9F%A9%E9%98%B5&oldid=52294204›.

Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
2020-04-12每天三百字之连接与替代冷眼看潮
不知道是不是好为人师，有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程，就是不断连接与替代的过程。人类发现了火并应用火以后，告别了茹毛饮血的野兽般的原始生活（火烧、烹饪替代了生食）人类用石器代替了完全手工，工具的使用使人类进步一大步。类似这样的替代还有很多，随着科技的发展，有更多的原始的事物被替代，代之以更高效、更先进的技术。在近现代，汽车替代了马车，高速公路和铁路
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
【JS】执行时长(100分) |思路参考+代码解析（C++） l939035548 JS 算法数据结构 c++
题目为了充分发挥GPU算力，需要尽可能多的将任务交给GPU执行，现在有一个任务数组，数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务，一次执行耗时1秒，在保证GPU不空闲情况下，最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数，取值范围[1,10000]第二个参数为任务数组长度，取值范围[1,10000]第三个参数为任务数组，数字范围
没有邀请码怎么注册买手妈妈? 氧惠评测
买手妈妈怎么注册小编为大家带来买手妈妈没有邀请码怎么注册。打开买手妈妈APP，点击“马上注册”，输入邀请信息“邀请码”点击下一步，没有邀请码是登录不上的，所以这个必须要填写，那我们没有怎么办？填写成功就可以登录下一步。这里面有手机登录和淘宝登录，手机登录以后也需要用淘宝授权的，所以基本上都是淘宝登录。购物、看电影、点外卖、用氧惠APP！更优惠！氧惠（全网优惠上氧惠）——是与以往完全不同的抖客+淘客
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
直返APP是什么?直返APP是干嘛的氧惠帮朋友一起省
直返是一种电商购物模式，其核心特点是用户购买商品后可以获得直接返利。具体来说，用户在直返电商平台购买商品时，不仅可以获得商品本身的优惠，还可以获得一定的现金返利或者积分奖励。返利的金额可以提现到用户的账户余额，或者用于下次购物时抵扣。氧惠APP（带货领导者）——是与以往完全不同的抖客+淘客app！2023全新模式，我的直推也会放到你下面。主打：带货高补贴，深受各位带货团队长喜爱（每天出单带货几十万
直返的东西正品吗?直返APP安全吗?直返是正规平台吗? 氧惠购物达人
亲们，你们是不是经常在直返APP上买东西呀？但是，你们有没有想过，里面的东西到底是不是正品呢？这个APP安全吗？它是不是一个正规的平台呀？别着急，今天我就来给大家揭秘一下！氧惠APP（带货领导者）——是与以往完全不同的抖客+淘客app！2023全新模式，我的直推也会放到你下面。主打：带货高补贴，深受各位带货团队长喜爱（每天出单带货几十万单）。注册即可享受高补贴+0撸+捡漏等带货新体验。送万元推广大
福袋生活邀请码在哪里填写，福袋生活app邀请码使用教程小小编007
很多人下载福袋生活后，注册使用时需要填写邀请码。因为福袋生活是注册邀请制，所以首次使用填写邀请码才可以正常登录使用。福袋生活是广州市福袋生活信息科技有限公司旗下一家多元化社交电商导购平台，以APP为载体，社群为媒介，汇集衣食住行、吃喝玩乐生活服务板块，使用福袋生活可以领到淘宝，拼多多等电商平台的商品优惠券和返利，还可以兼职去分享赚钱。我为什么从福袋生活转到果冻宝盒呢？当然是因为福袋生活返利更高，注
18、架构-可观测性之聚合度量大树~~ 架构 java python 后端架构
聚合度量聚合度量是指对系统运行时产生的各种指标数据进行收集、聚合和分析，以了解系统的健康状况和性能表现。聚合度量是可观测性的关键组成部分，通过对度量数据的分析，可以及时发现系统中的异常和瓶颈。以下是对聚合度量各个方面的详细解析，并结合具体的数据案例和技术支撑。指标收集收集系统运行时产生的各种指标数据是聚合度量的基础。常见的指标包括CPU使用率、内存使用率、请求处理时间、请求数、错误率等。以下是指标
读《人间鲁迅》有感琳语读书
上周读完《闻一多传》后，我对中国近代知识分子产生了兴趣，这周继续读了《人间鲁迅》。厚厚的两本书，记录了一个人的一生，苦痛，彷徨和挣扎，虽然只读了一小部分，却也心潮澎湃。闻一多和鲁迅是完全不同的。鲁迅是沉郁的，现实的，寂寞的，抗争的。除了天生性格的不同外，环境的塑造也是非常之大。鲁迅少年经历了家庭的变故，看尽了人间冷暖，世态炎凉。这种经历促使他很早就观察思考人生，立志用文学来改变中国国民的劣根。闻一
如何选择最适合你的项目研发管理软件？TAPD卓越版全面解析北京云巴巴信息技术有限公司产品经理需求分析
在当今快速发展的科技时代，项目研发管理软件已成为企业不可或缺的重要工具。面对市场上琳琅满目的产品，如何选择一款适合自己团队的项目研发管理软件呢？本文将围绕项目研发管理软件的选择标准，重点介绍TAPD卓越版的特点、优势以及使用体验，让你更好地理解和选择适合自己的项目研发管理软件。项目研发管理软件的选择标准在选择项目研发管理软件时，我们需要考虑以下几个方面的因素：功能全面性：软件是否覆盖了从需求管理、
剧本杀《鲸鱼马戏团》剧本杀剧透+真相答案复盘解析攻略 VX搜_奶茶剧本杀
本文为剧本杀《鲸鱼马戏团》剧本杀测评+部分真相复盘，获取完整真相复盘只需两步：①、关注微信公众号【奶茶剧本杀】→②、回复剧本杀《鲸鱼马戏团》即可获取查看剧本杀《鲸鱼马戏团》剧本杀真相答案复盘+凶手剧透：以下是玩家评测+部分关键证据，凶手，时间线，复盘解析，推理逻辑--------------------------------------------------------------------
简单了解 JVM 记得开心一点啊 jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称，意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统（如：JVM、VMwave、VirtualBox）。JVM和其他两个虚拟机
Java企业面试题3 马龙强_ java
1.break和continue的作用(智*图)break：用于完全退出一个循环（如for,while）或一个switch语句。当在循环体内遇到break语句时，程序会立即跳出当前循环体，继续执行循环之后的代码。continue：用于跳过当前循环体中剩余的部分，并开始下一次循环。如果是在for循环中使用continue，则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
戴容容中原焦点团队.网络初级第33期,坚持分享第19天 2022年3月9日 TessDai
《每个人眼中的世界都是不同的》“一千个人眼里有一千个哈姆雷特”世界是多元的,每个人都有自己的道理,人人按照自己的理解去看待这个世界的人和物.我们如此,其他人也是如此.因此,任何事情,我们要放下自己以为的真理,去理解他人认为的真理,只有同频方能共振.孩子在慢慢长大的过程中慢慢学会独立,甚至对抗.尤其当孩子处于青春期的时候,他们开始有很多自己独立的想法,和一些特立独行的做法,家长常常会觉得不可思议,觉
京券东券优惠券领取网站-点击进入高省爱氧惠
嘿，小伙伴们，你们知道吗？京东商城可是有好多超值优惠券等着我们领取哦！不论是京券还是东券，都有好多好多的优惠等着我们呢！氧惠APP（带货领导者）——是与以往完全不同的抖客+淘客app！2024全新模式，我的直推也会放到你下面。主打：带货高补贴，深受各位带货团队长喜爱（每天出单带货几十万单）。注册即可享受高补贴+0撸+捡漏等带货新体验。送万元推广大礼包，教你如何1年做到百万团队。想要领取这些优惠券，
辟谷日记备谷6 玉衡_李俊晔
备谷6图片发自App日期：18.1.31（周三）起床：7：30放假的日子，5：45的闹钟并没有关掉，每天也差不多这个点就朦朦胧胧醒了，有时不是真的醒了，就允许继续睡。今天似乎真的没什么睡意了——看来身体自然会有“够了”那个点，更加笃定：交托这词就是完完全全交托给身体，全然交托给宇宙，不需要任何评判，放下各种担心，恐惧，要求，内疚……在床上做逆转，思绪静不下来……知道成长就是做自己的主人，可以“掌控
ArrayList 源码解析程序猿进阶 Java基础 ArrayList List java 面试性能优化架构设计 idea
ArrayList是Java集合框架中的一个动态数组实现，提供了可变大小的数组功能。它继承自AbstractList并实现了List接口，是顺序容器，即元素存放的数据与放进去的顺序相同，允许放入null元素，底层通过数组实现。除该类未实现同步外，其余跟Vector大致相同。每个ArrayList都有一个容量capacity，表示底层数组的实际大小，容器内存储元素的个数不能多于当前容量。当向容器中添
Kafka是如何保证数据的安全性、可靠性和分区的喜欢猪猪 kafka 分布式
Kafka作为一个高性能、可扩展的分布式流处理平台，通过多种机制来确保数据的安全性、可靠性和分区的有效管理。以下是关于Kafka如何保证数据安全性、可靠性和分区的详细解析：一、数据安全性SSL/TLS加密：Kafka支持SSL/TLS协议，通过配置SSL证书和密钥来加密数据传输，确保数据在传输过程中不会被窃取或篡改。这一机制有效防止了中间人攻击，保护了数据的安全性。SASL认证：Kafka支持多种
Java爬虫框架（一）--架构设计狼图腾-狼之传说 java 框架 java 任务 html解析器存储电子商务
一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取，分析，存储，索引。爬虫：爬虫负责爬取，解析，处理电子商务网站的网页的内容数据库：存储商品信息索引：商品的全文搜索索引Task队列：需要爬取的网页列表Visited表：已经爬取过的网页列表爬虫监控平台：web平台可以启动，停止爬虫，管理爬虫，task队列，visited表。二、爬虫1.流程1)Scheduler启动爬虫器，TaskMast
光盘文件系统 (iso9660) 格式解析穷人小水滴光盘文件系统 iso9660 deno GNU/Linux javascript
越简单的系统,越可靠,越不容易出问题.光盘文件系统(iso9660)十分简单,只需不到200行代码,即可实现定位读取其中的文件.参考资料:https://wiki.osdev.org/ISO_9660相关文章:《光盘防水嘛?DVD+R刻录光盘泡水实验》https://blog.csdn.net/secext2022/article/details/140583910《光驱的内部结构及日常使用》ht
Spring MVC 全面指南：从入门到精通的详细解析一杯梅子酱技术栈学习 spring mvc java
引言：SpringMVC，作为Spring框架的一个重要模块，为构建Web应用提供了强大的功能和灵活性。无论是初学者还是有一定经验的开发者，掌握SpringMVC都将显著提升你的Web开发技能。本文旨在为初学者提供一个全面且易于理解的学习路径，通过详细的知识点分析和实际案例，帮助你快速上手SpringMVC，让学习过程既深刻又高效。一、SpringMVC简介1.1什么是SpringMVC？Spri
崩坏星穹铁道哪个角色值得培养崩坏星穹铁道新手角色优先级教学会飞滴鱼儿
崩坏星穹铁道新手角色培养攻略：哪些角色值得投资？在《崩坏星穹铁道》中，角色的强度和培养一直是玩家们关心的焦点。要想体验更爽快的游戏过程，选对角色至关重要。那么，哪些角色值得投资培养呢?本篇教学文章将针对新手玩家，从T0到T1强度的角色中为你做出详尽解析。游戏豹官网现在的手游平台很多，但是在游戏界有这么一个传说：“喜欢肝的玩家不如氪金玩家，氪金玩家不如内部福利玩家”，这就是游戏界可悲的生物链，很多平
WebMagic：强大的Java爬虫框架解析与实战 Aaron_945 Java java 爬虫开发语言
文章目录引言官网链接WebMagic原理概述基础使用1.添加依赖2.编写PageProcessor高级使用1.自定义Pipeline2.分布式抓取优点结论引言在大数据时代，网络爬虫作为数据收集的重要工具，扮演着不可或缺的角色。Java作为一门广泛使用的编程语言，在爬虫开发领域也有其独特的优势。WebMagic是一个开源的Java爬虫框架，它提供了简单灵活的API，支持多线程、分布式抓取，以及丰富的
【2022 CCF 非专业级别软件能力认证第一轮（CSP-J1）入门级 C++语言试题及解析】汉子萌萌哒 CCF noi 算法数据结构 c++
一、单项选择题(共15题，每题2分，共计30分；每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持：()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识，面向对象和类有关，类又涉及父类、子类、继承、派生等关系，printf
我家纱窗上全是杨树毛子 viiiiiiiiito
1“所以你脖…嘶…子上的伤不是你自己抓出来的喽？”永河喜欢在说话说到一半的时候吸烟，这总让他产生一些惊人的断句。”恩，不是给你说了么，方易在厕所门口就和别人打起来了，从厕所一路打到酒吧门口，他说我是去劝架，被误伤的。”“后来呢？”“后来就打车回家了啊。”“我是说打…嘶…架，赢了输了？“”完全不记得了，方易连他打的是谁都不知道，我看我这浑身疼的，估计是输了。“”垃圾，要不是我赶飞机昨天我们肯定…”“
python结束子进程_如何清除python中的子进程 weixin_39995943 python结束子进程
我们使用python进程来管理长时间运行的python子进程。有时需要终止子进程。kill命令不会完全终止进程，只会使其失效。运行以下脚本将演示此行为。importsubprocessp=subprocess.Popen(['sleep','400'],stdout=subprocess.PIPE,shell=False)或者p=subprocess.Popen('sleep400',stdout
绝招曝光！3小时高效利用ChatGPT写出精彩论文 kkai人工智能 chatgpt 人工智能 ai 学习媒体
在这份指南中，我将深入解析如何利用ChatGPT4.0的高级功能，指导整个学术研究和写作过程。从初步探索研究主题，到撰写结构严谨的学术论文，我将一步步展示如何在每个环节中有效运用ChatGPT。如果您还未使用PLUS版本，可以参考相关教程。**初步探索与主题的确定**起初，我处于庞大的知识领域中，寻找一个可深入研究的领域。ChatGPT如同灯塔，通过深入分析最新研究趋势和领域热点，帮助我在广阔的学
PHP，安卓，UI，java，linux视频教程合集 cocos2d-x小菜 java UI PHP android linux
╔-----------------------------------╗┆
各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。 bozch .net .net mvc
在.net mvc5中，在执行某一操作的时候，出现了如下错误：各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。经查询当前的操作与错误内容无关，经过对错误信息的排查发现，事故出现在数据库迁移上。回想过去：在迁移之前已经对数据库进行了添加字段操作，再次进行迁移插入XXX字段的时候，就会提示如上错误。 &
Java 对象大小的计算 e200702084 java
Java对象的大小如何计算一个对象的大小呢？
Mybatis Spring 171815164 mybatis
ApplicationContext ac = new ClassPathXmlApplicationContext("applicationContext.xml"); CustomerService userService = (CustomerService) ac.getBean("customerService"); Customer cust
JVM 不稳定参数 g21121 jvm
-XX 参数被称为不稳定参数，之所以这么叫是因为此类参数的设置很容易引起JVM 性能上的差异，使JVM 存在极大的不稳定性。当然这是在非合理设置的前提下，如果此类参数设置合理讲大大提高JVM 的性能及稳定性。可以说“不稳定参数”
用户自动登录网站永夜-极光用户
1.目标:实现用户登录后,再次登录就自动登录,无需用户名和密码 2.思路:将用户的信息保存为cookie 每次用户访问网站,通过filter拦截所有请求,在filter中读取所有的cookie,如果找到了保存登录信息的cookie,那么在cookie中读取登录信息,然后直接
centos7 安装后失去win7的引导记录程序员是怎么炼成的操作系统
1.使用root身份(必须)打开 /boot/grub2/grub.cfg 2.找到 ### BEGIN /etc/grub.d/30_os-prober ### 在后面添加 menuentry "Windows 7 (loader) (on /dev/sda1)" {
Oracle 10g 官方中文安装帮助文档以及Oracle官方中文教程文档下载 aijuans oracle
Oracle 10g 官方中文安装帮助文档下载：http://download.csdn.net/tag/Oracle%E4%B8%AD%E6%96%87API%EF%BC%8COracle%E4%B8%AD%E6%96%87%E6%96%87%E6%A1%A3%EF%BC%8Coracle%E5%AD%A6%E4%B9%A0%E6%96%87%E6%A1%A3 Oracle 10g 官方中文教程
JavaEE开源快速开发平台G4Studio_V3.2发布了無為子 AOP oracle mysql javaee G4Studio
我非常高兴地宣布,今天我们最新的JavaEE开源快速开发平台G4Studio_V3.2版本已经正式发布。大家可以通过如下地址下载。访问G4Studio网站 http://www.g4it.org G4Studio_V3.2版本变更日志功能新增 (1).新增了系统右下角滑出提示窗口功能。 (2).新增了文件资源的Zip压缩和解压缩
Oracle常用的单行函数应用技巧总结百合不是茶日期函数转换函数(核心)数字函数通用函数(核心)字符函数
单行函数; 字符函数,数字函数,日期函数,转换函数(核心),通用函数(核心) 一:字符函数: .UPPER(字符串) 将字符串转为大写 .LOWER (字符串) 将字符串转为小写 .INITCAP(字符串) 将首字母大写 .LENGTH (字符串) 字符串的长度 .REPLACE(字符串,'A','_') 将字符串字符A转换成_
Mockito异常测试实例 bijian1013 java 单元测试 mockito
Mockito异常测试实例： package com.bijian.study; import static org.mockito.Mockito.mock; import static org.mockito.Mockito.when; import org.junit.Assert; import org.junit.Test; import org.mockito.
GA与量子恒道统计 Bill_chen JavaScript 浏览器百度 Google 防火墙
前一阵子，统计**网址时，Google Analytics（GA）和量子恒道统计（也称量子统计），数据有较大的偏差，仔细找相关资料研究了下，总结如下：为何GA和量子网站统计（量子统计前身为雅虎统计）结果不同？首先：没有一种网站统计工具能保证百分之百的准确出现该问题可能有以下几个原因：（1）不同的统计分析系统的算法机制不同；（2）统计代码放置的位置和前后
【Linux命令三】Top命令 bit1129 linux命令
Linux的Top命令类似于Windows的任务管理器，可以查看当前系统的运行情况，包括CPU、内存的使用情况等。如下是一个Top命令的执行结果： top - 21:22:04 up 1 day, 23:49, 1 user, load average: 1.10, 1.66, 1.99 Tasks: 202 total, 4 running, 198 sl
spring四种依赖注入方式白糖_ spring
平常的java开发中，程序员在某个类中需要依赖其它类的方法，则通常是new一个依赖类再调用类实例的方法，这种开发存在的问题是new的类实例不好统一管理，spring提出了依赖注入的思想，即依赖类不由程序员实例化，而是通过spring容器帮我们new指定实例并且将实例注入到需要该对象的类中。依赖注入的另一种说法是“控制反转”，通俗的理解是：平常我们new一个实例，这个实例的控制权是我
angular.injector boyitech AngularJS AngularJS API
angular.injector 描述: 创建一个injector对象, 调用injector对象的方法可以获得angular的service, 或者用来做依赖注入. 使用方法: angular.injector(modules, [strictDi]) 参数详解: Param Type Details mod
java-同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待 bylijinnan Integer
public class PC { /** * 题目：生产者-消费者。 * 同步访问一个数组Integer[10]，生产者不断地往数组放入整数1000，数组满时等待；消费者不断地将数组里面的数置零，数组空时等待。 */ private static final Integer[] val=new Integer[10]; private static
使用Struts2.2.1配置 Chen.H apache spring Web xml struts
Struts2.2.1 需要如下 jar包: commons-fileupload-1.2.1.jar commons-io-1.3.2.jar commons-logging-1.0.4.jar freemarker-2.3.16.jar javassist-3.7.ga.jar ognl-3.0.jar spring.jar struts2-core-2.2.1.jar struts2-sp
[职业与教育]青春之歌 comsci 教育
每个人都有自己的青春之歌............但是我要说的却不是青春... 大家如果在自己的职业生涯没有给自己以后创业留一点点机会,仅仅凭学历和人脉关系,是难以在竞争激烈的市场中生存下去的.... &nbs
oracle连接(join)中使用using关键字 daizj JOIN oracle sql using
在oracle连接(join)中使用using关键字 34. View the Exhibit and examine the structure of the ORDERS and ORDER_ITEMS tables. Evaluate the following SQL statement: SELECT oi.order_id, product_id, order_date FRO
NIO示例 daysinsun nio
NIO服务端代码： public class NIOServer { private Selector selector; public void startServer(int port) throws IOException { ServerSocketChannel serverChannel = ServerSocketChannel.open(
C语言学习homework1 dcj3sjt126com c homework
0、课堂练习做完 1、使用sizeof计算出你所知道的所有的类型占用的空间。 int x; sizeof(x); sizeof(int); # include <stdio.h> int main(void) { int x1; char x2; double x3; float x4; printf(&quo
select in order by , mysql排序 dcj3sjt126com mysql
If i select like this: SELECT id FROM users WHERE id IN(3,4,8,1); This by default will select users in this order 1,3,4,8, I would like to select them in the same order that i put IN() values so:
页面校验-新建项目 fanxiaolong 页面校验
$(document).ready( function() { var flag = true; $('#changeform').submit(function() { var projectScValNull = true; var s =""; var parent_id = $("#parent_id").v
Ehcache（02）——ehcache.xml简介 234390216 ehcache ehcache.xml 简介
ehcache.xml简介 ehcache.xml文件是用来定义Ehcache的配置信息的，更准确的来说它是定义CacheManager的配置信息的。根据之前我们在《Ehcache简介》一文中对CacheManager的介绍我们知道一切Ehcache的应用都是从CacheManager开始的。在不指定配置信
junit 4.11中三个新功能 jackyrong java
junit 4.11中两个新增的功能，首先是注解中可以参数化，比如 import static org.junit.Assert.assertEquals; import java.util.Arrays; import org.junit.Test; import org.junit.runner.RunWith; import org.junit.runn
国外程序员爱用苹果Mac电脑的10大理由 php教程分享 windows PHP unix Microsoft perl
Mac 在国外很受欢迎，尤其是在设计/web开发/IT 人员圈子里。普通用户喜欢 Mac 可以理解，毕竟 Mac 设计美观，简单好用，没有病毒。那么为什么专业人士也对 Mac 情有独钟呢？从个人使用经验来看我想有下面几个原因： 1、Mac OS X 是基于 Unix 的这一点太重要了，尤其是对开发人员，至少对于我来说很重要，这意味着Unix 下一堆好用的工具都可以随手捡到。如果你是个 wi
位运算、异或的实际应用 wenjinglian 位运算
一．位操作基础，用一张表描述位操作符的应用规则并详细解释。二．常用位操作小技巧，有判断奇偶、交换两数、变换符号、求绝对值。三．位操作与空间压缩，针对筛素数进行空间压缩。 &n
weblogic部署项目出现的一些问题（持续补充中……） Everyday都不同 weblogic部署失败
好吧，weblogic的问题确实…… 问题一： org.springframework.beans.factory.BeanDefinitionStoreException: Failed to read candidate component class: URL [zip:E:/weblogic/user_projects/domains/base_domain/serve
tomcat7性能调优（01） toknowme tomcat7
Tomcat优化： 1、最大连接数最大线程等设置 <Connector port="8082" protocol="HTTP/1.1" useBodyEncodingForURI="t
PO VO DAO DTO BO TO概念与区别 xp9802 java DAO 设计模式 bean 领域模型
O/R Mapping 是 Object Relational Mapping（对象关系映射）的缩写。通俗点讲，就是将对象与关系数据库绑定，用对象来表示关系数据。在O/R Mapping的世界里，有两个基本的也是重要的东东需要了解，即VO，PO。它们的关系应该是相互独立的，一个VO可以只是PO的部分，也可以是多个PO构成，同样也可以等同于一个PO（指的是他们的属性）。这样，PO独立出来，数据持

多元高斯分布完全解析

摘要

多元标准高斯分布

多元高斯分布

多元高斯分布的几何意义

总结

你可能感兴趣的:(多元高斯分布完全解析)