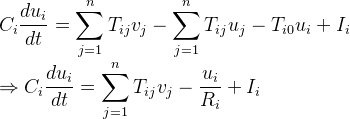PrivateEye_zzy
PrivateEye_zzy

TSP问题—Hopfield神经网络算法

本章涉及知识点

1、生物神经元的结构

2、Hopfield神经网络结构

3、神经动力学

4、CHNN的网络结构

5、一般性CHNN模型的状态方程推导

6、一般性CHNN模型的能量方程定义

7、CHNN模型下TSP的置换矩阵设计

8、CHNN模型下TSP的能量方程定义

9、CHNN模型下TSP的能量方程和状态方程的优化

10、CHNN模型下TSP输入状态和输出状态的更新方法

11、Hopfield求解TSP问题的步骤

12、python编程实现Hopfield

13、结果分析

一、生物神经元的结构

TSP问题—Hopfield神经网络算法_第1张图片
生物神经元

人类的大脑，有着大约860亿个神经元，而神经元，是构成神经网络系统结构和功能的基本单位，其主要构成成分包括树突、胞体、轴突和细胞膜等

神经元的主要功能是接受外界或不同神经元的信号刺激，产生兴奋或者抑制的神经冲动，并通过突触传递到下一个神经元进行信息交互

我们需要知道以下几个生物神经元的名词概念

（1）树突：从胞体发出的一个至多个突起，呈放射状，用来接受外界的刺激

（2）轴突：每个神经元有且只有一个轴突，用来向外界输出神经冲动

（3）突触：将一个神经元的神经冲动，传递到另一个神经元的相互接触的结构

从上述的概念可以看出：一个生物神经元可以接受多组输入，产生单组输出，且输入输出呈非线性关系

我们通过对神经元和神经网络进行数学建模，用计算机来尽量模拟生物神经网络的学习和思考过程，这样的网络叫做人工神经网络（ANN），ANN按照信息流可以分为前馈式和后馈式

这章研究的Hopfield神经网络就属于反馈式神经网络

二、Hopfield神经网络结构

Hopfield神经网络有如下特点

（1）每个神经元既是输入也是输出，构成单层全连接递归网络

（2）网络的突触权值不同于其他的神经网络是通过有监督或无监督反复学习来获得，而是在搭建网络时就按照一定的规则计算出来，且网络的权值在整个网络迭代过程中不再改变

（3）网络的状态是随时间的变化而变化的，每个神经元在t时刻的输出状态和自己t-1时刻有关

（4）引入能量函数的概念，用来判断网络迭代的稳定性，即网络的收敛，就是指能量函数达到极小值

（5）网络的解，即是网络运行到稳定时，各个神经元的状态集合

TSP问题—Hopfield神经网络算法_第2张图片
反馈式神经网络的结构图

Hopfield神经网络也是递归神经网络（RNN）的前身，Hopfield模型分为：

离散型（DHNN）：适用于处理联想记忆问题

连续性（CHNN）：适用于处理组合优化问题

三、神经动力学

神经动力学的定义：将神经网络看做是一种非线性动力学系统，系统的状态集合随时间的变化而变化

令系统的输出状态变量集合为

状态变量集合

其中t是连续时间变量，则系统的输出状态和输出状态的增量可以用下面的微分方程表示

动力系统的微分方程

其中F函数是S型非线性函数映射，一般F取对称sigmoid双曲正切函数来完成输出状态的非线性映射

双曲正切函数

四、CHNN的网络结构

TSP问题是组合优化，使用Hopfield神经网络的CHNN模型，将网络抽象为

（1）Hopfield神经网络等效为放大电子电路

（2）Hopfield每一个神经元等效为一个电子放大器元件

（3）Hopfield每一个神经元的输入和输出，等效为电子元件的输入电压和输出电压

（4）每一个电子元件（神经元）输出的电信号有正负值，正值代表兴奋，负值代表抑制

（5）每一个电子元件（神经元）的输入信息，包含恒定的外部电流输入，和其它电子元件的反馈连接

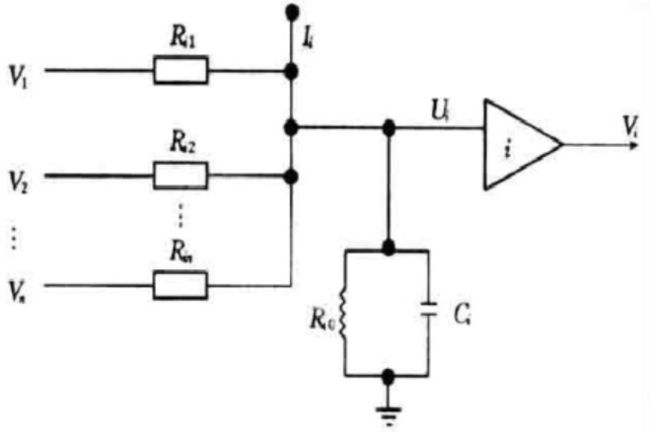
根据以上等效抽象，CHNN的电路拓扑图结构为

TSP问题—Hopfield神经网络算法_第3张图片
CHNN的等效电路图

其中，Ui表示放大电子元件的输入电压，Vi表示输出电压，运算放大器i表示第i个神经元

五、一般性CHNN模型的状态方程推导

设电容C两端的电压为Uc，存储的电荷量为Q，则

电容量

则经过电容C的电流为

电容C的电流

根据基尔霍夫电流定律，CHNN等效电路的电流关系为

基尔霍夫电流定律

令Tij表示神经元之间连接的权值

神经元之间连接的权值

则电流关系化简为

TSP问题—Hopfield神经网络算法_第4张图片
CHNN模型的状态方程

上式就是关于CHNN模型中输入电压ui和ui增量的微分方程关系，也就是CHNN模型的状态方程，其中输入电压vi满足非线性映射规则f

输出电压的非线性映射

六、一般性CHNN模型的能量方程定义

在神经网络的优化过程中，目标函数是用来判断当前网络是否达到稳定，即网络的优化，就是目标函数逼近达到最小值的过程，一般的优化算法有：梯度下降法、牛顿法、启发式优化等

但是在Hopfield网络中，由于网络的权重全程保持不变，神经元当前时刻状态和上一个时刻相关，为此我们采用能量函数来衡量Hopfield网络的稳定性

由于CHNN的能量函数定义为

CHNN的能量函数

能量函数E是单调下降，故Hopfield网络是稳定的

至此，有了Hopfield网络的CHNN模型的状态方程和能量函数，我们就可以来尝试抽象和转化TSP问题

七、CHNN模型下TSP的置换矩阵设计

我们的案例里有8个城市，通过构造NN模型，将每一个城市对应于神经网络的每一个神经元，即案例的TSP问题可以用8x8=64个神经元组成的Hopfield网络来求解

为了满足TSP的规则，我们设计置换矩阵的形式如下

TSP问题—Hopfield神经网络算法_第5张图片
TSP的置换矩阵

置换矩阵负责翻译并遵从TSP的规则：

（1）一个城市只能被访问一次，翻译为：矩阵每行有且只有一个1，其余元素均为0

（2）一次只能访问一个城市，翻译为：矩阵每列有且只有一个1，其余元素均为0

（3）共访问过n个城市，翻译为：矩阵的全部元素中1的数量为n

在神经网络迭代优化过程中，每次神经元输出的状态集合只要满足上述置换矩阵的规则，则证明该组输出状态就是一个TSP问题的解，我们只要在这些解中找到最小代价的解即可

八、CHNN模型下TSP的能量方程定义

对于TSP问题，我们在一般性CHNN能量函数的基础上，需要考虑以下两点问题来设计出TSP的能量函数

（1）TSP的能量函数需要量化的翻译置换矩阵的规则

（2）在TSP问题中的n!个合法路线中，能量函数要有利于量化表示最短路线的解

为此，我们设计TSP能量函数的第一项为

TSP能量函数的第一项

上式翻译为：每一行中的每一个城市x，必须有且只有一个1，符合置换矩阵的第一条规则

设计TSP能量函数的第二项为

TSP能量函数的第二项

上式翻译为：每一列中的每一个城市x，必须有且只有一个1，符合置换矩阵的第二条规则

设计TSP能量函数的第三项为

TSP能量函数的第三项

上式翻译为：整个矩阵有n个1，符合置换矩阵的第三条规则

设计TSP能量函数的第四项为

TSP能量函数的第四项

上式包含神经网络输出中有效解的路径长度信息，dxy表示城市x到城市y的距离

为此，TSP的能量函数E整合为

TSP问题—Hopfield神经网络算法_第6张图片
TSP的能量函数E

其中参数ABCD称为权值，前三项是满足TSP置换矩阵的约束条件，最后一项包含优化目标函数项

九、CHNN模型下TSP的能量方程和状态方程的优化

由于上式定义的能量函数过于复杂，数学家们对能量函数进行了优化，将TSP问题的能量函数改进为

TSP的能量函数E的改进

优化后的能量函数减少了权值参数的个数，且根据能量函数E，将CHNN的动态方程优化为

TSP问题—Hopfield神经网络算法_第7张图片
CHNN的动态方程的优化

在实际编程中，我们可以用这两个函数优化迭代和判定当前Hopfield神经网络的输出状态

十、CHNN模型下TSP输入状态和输出状态的更新方法

我们根据优化后CHNN的动态方程，可以写出Hopfield递归神经网络的输入状态的更新表达式为

输入状态的更新表达式

上式中可以看到Hopfield递归神经网络当前时刻的输入与其上一个时刻关联

由非线性映射，我们写出Hopfield递归神经网络的输出状态的更新表达式为

输出状态的更新表达式

其中输出状态的非线性映射是双曲正切函数

十一、Hopfield求解TSP问题的步骤

至此，我们总结出利用Hopfield神经网络来求解TSP问题的步骤

（1）初始化Hopfield神经网络的初值（如输入电压U0、迭代次数）和权值（A、D）

（2）计算n个城市之间的距离矩阵Dxy

（3）初始化神经网络的输入状态

初始化神经网络的输入状态

其中加入的随机项为

随机项

（4）利用CHNN动态方程计算输入状态的增量

输入状态的增量

（5）由一阶欧拉方法更新神经网络下一个时刻的输入状态

更新下一个时刻的输入状态

（6）由sigmoid函数更新神经网络下个时刻的输出状态

更新下一个时刻的输出状态 

（7）计算当前的能量函数E

计算能量函数E

（8）检查当前神经网络的输出状态集合，是否满足TSP置换矩阵的规则

十二、python编程实现Hopfield

我们用python编程实现出Hopfield神经网络的优化步骤

动态方程计算微分方程du

TSP问题—Hopfield神经网络算法_第8张图片
动态方程计算微分方程du

更新神经网络的输入电压U

更新神经网络的输入电压U

更新神经网络的输出电压V

更新神经网络的输出电压V

计算当前网络的能量

TSP问题—Hopfield神经网络算法_第9张图片
计算当前网络的能量

检查路径的正确性

TSP问题—Hopfield神经网络算法_第10张图片
检查路径的正确性

迭代优化Hopfield神经网络

TSP问题—Hopfield神经网络算法_第11张图片
迭代优化Hopfield神经网络

十三、结果分析

我们设置以下参数来求解TSP案例

TSP问题—Hopfield神经网络算法_第12张图片
初值设置

根据这些初值，Hopfield神经网络在经过10000次迭代优化后，找到的TSP的最优路线解为

TSP问题—Hopfield神经网络算法_第13张图片
Hopfield网络找到的TSP路线

最终Hopfield神经网络找到的最优哈密顿回路为

TSP问题—Hopfield神经网络算法_第14张图片
Hopfield神经网络找到的最优哈密顿回路

可以看到初值设置得当，Hopfield神经网络找到的最优解已经和真实最优解一致

在神经网络优化过程中，能量函数的波动为

TSP问题—Hopfield神经网络算法_第15张图片
能量函数的波动

用Hopfield神经网络求解TSP问题，我们可以总结出以下几点

（1）Hopfield神经网络是求解TSP的一种优化网络算法

（2）Hopfield神经网络通过神经动力学来映射生物神经网络，在参数设置合理的情况下，有可能找到真实最优解，比近似算法计算的效果要好

（3）Hopfield神经网络比较依赖初始权值的设置，会受到初始输入状态和输出状态的随机性影响，不一定每一次都可以找到最优解，有可能找到的是不同的次优解

案例代码见：Hopfield神经网络求解TSP问题

你可能感兴趣的:(TSP问题—Hopfield神经网络算法)

  • 斤斤计较的婚姻到底有多难？ 白心之岂必有为
    很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
  • 关于沟通这件事，项目经理不需要每次都面对面进行 流程大师兄
    很多项目经理都会遇到这样的问题，项目中由于事情太多，根本没有足够的时间去召开会议，那在这种情况下如何去有效地管理项目中的利益相关者？当然，不建议电子邮件也不需要开会的话，建议可以采取下面几种方式来形成有效的沟通，这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题，项目中哪些利益相关者是必须要进行沟通的？可以列出项目中所有的利益相关者清单，同时也整理出项目中哪些
  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 2020-01-25 晴岚85
    郑海燕坚持分享590天2020.1.24在生活中只存在两个问题。一个问题是：你知道想要达成的目标是什么，但却不知道如何才能达成；另一个问题是：你不知道你的目标是什么。前一个是行动的问题，后一个是结果的问题。通过制定具体的下一步行动，可以解决不知道如何开始行动的问题。而通过去想象结果，对结果做预估，可以解决找不着目标的问题。对于所有吸引我们注意力，想要完成的任务，你可以先想象一下，预期的结果究竟是什
  • 小丽成长记（四十三） 玲玲54321
    小丽发现，即使她好不容易调整好自己的心态下一秒总会有不确定的伤脑筋的事出现，一个接一个的问题，人生就没有停下的时候，小问题不断出现。不过她今天看的书，她接受了人生就是不确定的，厉害的人就是不断创造确定性，在Ta的领域比别人多的确定性就能让自己脱颖而出，显示价值从而获得的比别人多的利益。正是这样的原因，因为从前修炼自己太少，使得她现在在人生道路上打怪起来困难重重，她似乎永远摆脱不了那种无力感，有种习
  • 学点心理知识，呵护孩子健康 静候花开_7090
    昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
  • Long类型前后端数据不一致 igotyback 前端
    响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
  • 如何在 Fork 的 GitHub 项目中保留自己的修改并同步上游更新？github_fork_update iBaoxing github
    如何在Fork的GitHub项目中保留自己的修改并同步上游更新？在GitHub上Fork了一个项目后，你可能会对项目进行一些修改，同时原作者也在不断更新。如果想要在保留自己修改的基础上，同步原作者的最新更新，很多人会不知所措。本文将详细讲解如何在不丢失自己改动的情况下，将上游仓库的更新合并到自己的仓库中。问题描述假设你在GitHub上Fork了一个项目，并基于该项目做了一些修改，随后你发现原作者对
  • 本周第二次约练 2cfbdfe28a51
    中原焦点团队中24初26刘霞2021.12.3约练161次，分享第368天当事人虽然是带着问题来的，但是咨询过程中发现，她是经过自己不断地调整和努力才走到现在的，看到当事人的不容易，找到例外，发现资源，力量感也就随之而来。增强画面感，或者说重温，会给当事人带来更深刻的感受。
  • 怎么起诉借钱不还的人？怎样起诉欠款不还的人？ 影子爱学习
    怎么起诉借钱不还的人？怎样起诉欠款不还的人？如果遇到难以解决的法律问题，我们可以匹配专业律师。例如：婚姻家庭（离婚纠纷）、刑事辩护、合同纠纷、债权债务、房产（继承）纠纷、交通事故、劳动争议、人身损害、公司相关法律事务（法律顾问）等咨询推荐手机/微信:15633770876【全国案件皆可】借钱不还起诉对方需要哪些资料起诉欠钱不还的，一般需要的材料包括以下这些：借据、收据、欠条、付款凭证等证据，以及向
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 2020.11.19 隆非凡
    日精进，今日体验：在维修过程中遇到的问题，把源头找到，在进行下一步开始。不要停留在一个点上，合理调整心态，把当下事做好。
  • 使用 FinalShell 进行远程连接（ssh 远程连接 Linux 服务器） 编程经验分享 开发工具服务器sshlinux
    目录前言基本使用教程新建远程连接连接主机自定义命令路由追踪前言后端开发，必然需要和服务器打交道，部署应用，排查问题，查看运行日志等等。一般服务器都是集中部署在机房中，也有一些直接是云服务器，总而言之，程序员不可能直接和服务器直接操作，一般都是通过ssh连接来登录服务器。刚接触远程连接时，使用的是XSHELL来远程连接服务器，连接上就能够操作远程服务器了，但是仅用XSHELL并没有上传下载文件的功能
  • 18-115 一切思考不能有效转化为行动，都TM是扯淡！ 成长时间线
    7月25号写了一篇关于为什么会断更如此严重的反思，然而，之后日更仅仅维持了一周，又出现了这次更严重的现象。从8月2号到昨天8月6号，5天！又是5天没有更文！虽然这次断更时间和上次一样，那为什么说这次更严重？因为上次之后就分析了问题的原因，以及应该如何解决，按理说应该会好转，然而，没过几天严重断更的现象再次出现，想想，经过反思，问题依然没有解决与改变，这让我有些担忧。到底是哪里出了问题，难道我就真的
  • 山东大学小树林支教调研团青青仓木队——翟晓楠 山东大学青青仓木队
    过了半年，又一次启程，又一次回到支教的初心之地。比起上一次的试探与不安，我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同，半个学期中，身体上的，心理上的，太多的逆境让我变得步履维艰，曲曲折折，弯弯绕绕，我仿佛打不起精神，没有胃口，没有动力。感觉走的不顺畅的时候，支教这个旅程，给了我力量。自告奋勇承担起队长这一职务的我，从组织时的复杂和困难的经历，协调各种问题，从无到有，和校长和队
  • 【夜读】提升生活品质的8个建议 茳淮秀水
    停止攀比很多人之所以感觉疲惫，部分原因是来自于跟别人攀比。殊不知，攀比得到的满足只是片刻的，过后往往会感到空虚。过分在意别人的评价，丢失的是自己原有的审美，扰乱的是自己最初的节奏。不妨活得洒脱些，自己内心丰盈了，快乐就能更持久。停止自责想改变自己，先从接纳自己开始。越是过分自责，就越难改变现状，因为如果把精力全耗在自责上，就没有精力用来改变了。遇到问题，我们要用正确的心态去面对。与其一味自责，不如
  • 蘩漪：新女性？利己主义者 赮_红雨
    蘩漪是曹禺《雷雨》笔下的女性形象。对于她的喜爱，曹禺在之前的访谈中，就已经表达得很清楚了，蘩漪是他所倾心的女子的“代替者”。在这个女性身上有着曹禺最精心的描写，但同时她的身上又存在着一些时代的问题。图片发自App首先，繁漪是追求自由和幸福的新女性形象。她是精神悲剧的核心人物，她对周朴园的反抗，具有典型意义。她是位资产阶级家庭出身的小姐，受过五四新思潮的影响，她任性、傲慢，追求人格独立、个性自由和爱
  • 如果做到轻松在股市赚钱？只要坚持这三个原则。 履霜之人
    大A股里向来就有七亏二平一赚的说法，能赚钱的都是少数人。否则股市就成了慈善机构，人人都有钱赚，谁还要上班？所以说亏钱是正常的，或者说是应该的。那么那些赚钱的人又是如何做到的呢？普通人能不能找到捷径去分一杯羹呢？方法是有的，但要做到需要你有极高的自律。第一，控制仓位，散户最大的问题是追涨杀跌，只要涨起来，就把钱往股票上砸，然后被套，隔天跌的受不了，又一刀切，全部割肉。来来回回间，遍体鳞伤。所以散户首
  • 利用LangChain的StackExchange组件实现智能问答系统 nseejrukjhad langchainmicrosoft数据库python
    利用LangChain的StackExchange组件实现智能问答系统引言在当今的软件开发世界中，StackOverflow已经成为程序员解决问题的首选平台之一。而LangChain作为一个强大的AI应用开发框架，提供了StackExchange组件，使我们能够轻松地将StackOverflow的海量知识库集成到我们的应用中。本文将详细介绍如何使用LangChain的StackExchange组件
  • 想明白这个问题，你才能写下去 文自拾
    春节放假的时候，又有一天梦见她，第二天她冒着漫天大雪，傻傻地跑来见我。她说，见见傻傻的我，天很冷，心很暖。她回去后，我写了一篇文章，题目叫——从此梦中只有你。我们没在一起的很长一段时间里，她都在我的心底，一次次出现在我的梦里。我对她说，在一起之前，是胆小且闷骚，在一起之后，我变得不要脸了。不要脸的——去爱你。那文章没写完，火车上，给她看了。我有点小失望，花了好几个小时写，她分分钟就看完，很希望她逐
  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 把握“三度”打造“三有”干部队伍 辛德瑞拉卡卡卡
    “胜败兴亡之分，不得不归咎于人事也”。干部队伍建设工作的好坏，关系到党和国家的发展全局。近日，新疆维吾尔自治区党委书记马兴瑞在部分党群单位走访调研时强调，要努力培养造就忠诚干净担当的高素质专业化干部队伍。各级组织部门应当在培养选拔干部、吸收优秀青年到党内来、培养造就优秀人才上下功夫，切实增强干部投身实践、解决问题、推进工作的能力，着力打造高素质专业化干部队伍。“天生我材必有用”，增强选育有“准度”
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • Kafka 消息丢失如何处理？ 架构文摘JGWZ 学习
    今天给大家分享一个在面试中经常遇到的问题：Kafka消息丢失该如何处理？这个问题啊，看似简单，其实里面藏着很多“套路”。来，咱们先讲一个面试的“真实”案例。面试官问：“Kafka消息丢失如何处理？”小明一听，反问：“你是怎么发现消息丢失了？”面试官顿时一愣，沉默了片刻后，可能有点不耐烦，说道：“这个你不用管，反正现在发现消息丢失了，你就说如何处理。”小明一头雾水：“问题是都不知道怎么丢的，处理起来
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • libyuv之linux编译 jaronho Linuxlinux运维服务器
    文章目录一、下载源码二、编译源码三、注意事项1、银河麒麟系统（aarch64）（1）解决armv8-a+dotprod+i8mm指令集支持问题（2）解决armv9-a+sve2指令集支持问题一、下载源码到GitHub网站下载https://github.com/lemenkov/libyuv源码，或者用直接用git克隆到本地，如：gitclonehttps://github.com/lemenko
  • 走向以教育叙事为载体的教育叙事研究 666小飞鱼
    今天我读了吴松超老师的《给教师的68条建写作建议》中的第23条《如何通过教育叙事走向研究》，吴老师在文中与我们分享了一个德育案例，这是一个反面的案例，意在告知我们在处理问题时，不能就考虑的点太窄，思考要全面。走向教育叙事研究，教师要有敏锐的“感知力”，这个感知力来自于背后专业知识的支撑，思维能力以及广阔的视野和见识等。所以对于同一件事处理方法不同，这个就是教师背后“敏锐力”的不同造成的，也就是说是
  • 2023-10-22 奥雷里亚诺第n
    昨天在B站看到关于猫喜欢挠人的视频，视频教导说猫挠人的话就抓住它的后脖颈然后用手打打挠人的那个爪子。视频本身没什么，但评论区却炸开了锅（真是符合挑食者厌食心理）。令我印象最深刻的一个甚至上升到了关于我是谁这种终极问题。它说，猫就是畜生，它挠人就打它别惯着它，反正我六道轮回成了人就应该保持人的高贵，谁都别想来打破。我顿时汗颜，但看到下面全是类似的言论只不过后面的理由各有不同，本来想骂人的心都凉了一半
  • 梁文道《尽头:怎样是好的阅读和书写》 片段 白夜书摘
    1、写小说的人，有时会强烈地感到一种现实的召唤，想去面对和回应现实。这时他们会觉得自己正站在时代中心，就像黑格尔说的，要把时代精神掌握在自己的小说（不是哲学）里面。但是这也很危险，当一个作家像一个时代那样书写，可能就会出现问题了。2、文字是远比语言大块而且湿冷的木头，又距离我们内心的火花稍远，不容易瞬间点燃起来，这处隙缝，给了我们回身的余地，可以再多看一下想一下设身处地一下；人类过往这最后五千年，
  • HQL之投影查询 归来朝歌 HQLHibernate查询语句投影查询
            在HQL查询中，常常面临这样一个场景，对于多表查询，是要将一个表的对象查出来还是要只需要每个表中的几个字段，最后放在一起显示？ 针对上面的场景，如果需要将一个对象查出来： HQL语句写“from 对象”即可 Session session = HibernateUtil.openSession();
  • Spring整合redis bylijinnan redis
    pom.xml <dependencies> <!-- Spring Data - Redis Library --> <dependency> <groupId>org.springframework.data</groupId> <artifactId>spring-data-redi
  • org.hibernate.NonUniqueResultException: query did not return a unique result: 2 0624chenhong Hibernate
    参考：http://blog.csdn.net/qingfeilee/article/details/7052736 org.hibernate.NonUniqueResultException: query did not return a unique result: 2         在项目中出现了org.hiber
  • android动画效果 不懂事的小屁孩 android动画
    前几天弄alertdialog和popupwindow的时候，用到了android的动画效果，今天专门研究了一下关于android的动画效果，列出来，方便以后使用。 Android 平台提供了两类动画。 一类是Tween动画，就是对场景里的对象不断的进行图像变化来产生动画效果（旋转、平移、放缩和渐变）。 第二类就是 Frame动画，即顺序的播放事先做好的图像，与gif图片原理类似。
  • js delete 删除机理以及它的内存泄露问题的解决方案 换个号韩国红果果 JavaScript
    delete删除属性时只是解除了属性与对象的绑定，故当属性值为一个对象时，删除时会造成内存泄露  （其实还未删除） 举例： var person={name:{firstname:'bob'}} var p=person.name delete person.name p.firstname -->'bob' // 依然可以访问p.firstname，存在内存泄露
  • Oracle将零干预分析加入网络即服务计划 蓝儿唯美 oracle
    由Oracle通信技术部门主导的演示项目并没有在本月较早前法国南斯举行的行业集团TM论坛大会中获得嘉奖。但是，Oracle通信官员解雇致力于打造一个支持零干预分配和编制功能的网络即服务（NaaS）平台，帮助企业以更灵活和更适合云的方式实现通信服务提供商（CSP）的连接产品。这个Oracle主导的项目属于TM Forum Live!活动上展示的Catalyst计划的19个项目之一。Catalyst计
  • spring学习——springmvc（二） a-john springMVC
    Spring MVC提供了非常方便的文件上传功能。 1，配置Spring支持文件上传： DispatcherServlet本身并不知道如何处理multipart的表单数据，需要一个multipart解析器把POST请求的multipart数据中抽取出来，这样DispatcherServlet就能将其传递给我们的控制器了。为了在Spring中注册multipart解析器，需要声明一个实现了Mul
  • POJ-2828-Buy Tickets aijuans ACM_POJ
    POJ-2828-Buy Tickets http://poj.org/problem?id=2828 线段树，逆序插入 #include<iostream>#include<cstdio>#include<cstring>#include<cstdlib>using namespace std;#define N 200010struct
  • Java Ant build.xml详解 asia007 build.xml
    1,什么是antant是构建工具2,什么是构建概念到处可查到，形象来说，你要把代码从某个地方拿来，编译，再拷贝到某个地方去等等操作，当然不仅与此，但是主要用来干这个3,ant的好处跨平台   --因为ant是使用java实现的，所以它跨平台使用简单--与ant的兄弟make比起来语法清晰--同样是和make相比功能强大--ant能做的事情很多，可能你用了很久，你仍然不知道它能有
  • android按钮监听器的四种技术 百合不是茶 androidxml配置监听器实现接口
    android开发中经常会用到各种各样的监听器,android监听器的写法与java又有不同的地方;    1,activity中使用内部类实现接口 ,创建内部类实例  使用add方法  与java类似   创建监听器的实例 myLis lis = new myLis();   使用add方法给按钮添加监听器  
  • 软件架构师不等同于资深程序员 bijian1013 程序员架构师架构设计
            本文的作者Armel Nene是ETAPIX Global公司的首席架构师，他居住在伦敦，他参与过的开源项目包括 Apache Lucene,，Apache Nutch， Liferay 和 Pentaho等。         如今很多的公司
  • TeamForge Wiki Syntax & CollabNet User Information Center sunjing TeamForgeHow doAttachementAnchorWiki Syntax
    the CollabNet user information center http://help.collab.net/   How do I create a new Wiki page? A CollabNet TeamForge project can have any number of Wiki pages. All Wiki pages are linked, and
  • 【Redis四】Redis数据类型 bit1129 redis
    概述 Redis是一个高性能的数据结构服务器，称之为数据结构服务器的原因是，它提供了丰富的数据类型以满足不同的应用场景，本文对Redis的数据类型以及对这些类型可能的操作进行总结。 Redis常用的数据类型包括string、set、list、hash以及sorted set.Redis本身是K/V系统，这里的数据类型指的是value的类型，而不是key的类型，key的类型只有一种即string
  • SSH2整合-附源码 白糖_ eclipsespringtomcatHibernateGoogle
    今天用eclipse终于整合出了struts2+hibernate+spring框架。 我创建的是tomcat项目，需要有tomcat插件。导入项目以后，鼠标右键选择属性，然后再找到“tomcat”项，勾选一下“Is a tomcat project”即可。具体方法见源码里的jsp图片，sql也在源码里。     补充1：项目中部分jar包不是最新版的，可能导
  • [转]开源项目代码的学习方法 braveCS 学习方法
    转自： http://blog.sina.com.cn/s/blog_693458530100lk5m.html http://www.cnblogs.com/west-link/archive/2011/06/07/2074466.html   1）阅读features。以此来搞清楚该项目有哪些特性2）思考。想想如果自己来做有这些features的项目该如何构架3）下载并安装d
  • 编程之美-子数组的最大和（二维） bylijinnan 编程之美
    package beautyOfCoding; import java.util.Arrays; import java.util.Random; public class MaxSubArraySum2 { /** * 编程之美 子数组之和的最大值（二维） */ private static final int ROW = 5; private stat
  • 读书笔记-3 chengxuyuancsdn jquery笔记resultMap配置ibatis一对多配置
    1、resultMap配置 2、ibatis一对多配置 3、jquery笔记 1、resultMap配置 当<select resultMap="topic_data"> <resultMap id="topic_data">必须一一对应。 (1)<resultMap class="tblTopic&q
  • [物理与天文]物理学新进展 comsci
          如果我们必须获得某种地球上没有的矿石,才能够进行某些能量输出装置的设计和建造,而要获得这种矿石,又必须首先进行深空探测,而要进行深空探测,又必须获得这种能量输出装置,这个矛盾的循环,会导致地球联盟在与宇宙文明建立关系的时候,陷入困境       怎么办呢?  
  • Oracle 11g新特性:Automatic Diagnostic Repository daizj oracleADR
    Oracle Database 11g的FDI（Fault Diagnosability Infrastructure）是自动化诊断方面的又一增强。 FDI的一个关键组件是自动诊断库（Automatic Diagnostic Repository-ADR）。 在oracle 11g中，alert文件的信息是以xml的文件格式存在的，另外提供了普通文本格式的alert文件。 这两份log文
  • 简单排序:选择排序 dieslrae 选择排序
    public void selectSort(int[] array){ int select; for(int i=0;i<array.length;i++){ select = i; for(int k=i+1;k<array.leng
  • C语言学习六指针的经典程序，互换两个数字 dcj3sjt126com c
    示例程序，swap_1和swap_2都是错误的，推理从1开始推到2，2没完成，推到3就完成了 # include <stdio.h> void swap_1(int, int); void swap_2(int *, int *); void swap_3(int *, int *); int main(void) { int a = 3; int b =
  • php 5.4中php-fpm 的重启、终止操作命令 dcj3sjt126com PHP
    php 5.4中php-fpm 的重启、终止操作命令: 查看php运行目录命令：which php/usr/bin/php 查看php-fpm进程数：ps aux | grep -c php-fpm 查看运行内存/usr/bin/php  -i|grep mem 重启php-fpm/etc/init.d/php-fpm restart 在phpinfo()输出内容可以看到php
  • 线程同步工具类 shuizhaosi888 同步工具类
    同步工具类包括信号量（Semaphore）、栅栏（barrier）、闭锁（CountDownLatch）   闭锁（CountDownLatch） public class RunMain { public long timeTasks(int nThreads, final Runnable task) throws InterruptedException { fin
  • bleeding edge是什么意思 haojinghua DI
    不止一次，看到很多讲技术的文章里面出现过这个词语。今天终于弄懂了——通过朋友给的浏览软件，上了wiki。  我再一次感到，没有辞典能像WiKi一样，给出这样体贴人心、一清二楚的解释了。为了表达我对WiKi的喜爱，只好在此一一中英对照，给大家上次课。   In computer science, bleeding edge is a term that
  • c中实现utf8和gbk的互转 jimmee ciconvutf8&gbk编码
    #include <iconv.h> #include <stdlib.h> #include <stdio.h> #include <unistd.h> #include <fcntl.h> #include <string.h> #include <sys/stat.h> int code_c
  • 大型分布式网站架构设计与实践 lilin530 应用服务器搜索引擎
    1.大型网站软件系统的特点？ a.高并发，大流量。 b.高可用。 c.海量数据。 d.用户分布广泛，网络情况复杂。 e.安全环境恶劣。 f.需求快速变更，发布频繁。 g.渐进式发展。 2.大型网站架构演化发展历程？ a.初始阶段的网站架构。 应用程序，数据库，文件等所有的资源都在一台服务器上。 b.应用服务器和数据服务器分离。 c.使用缓存改善网站性能。 d.使用应用
  • 在代码中获取Android theme中的attr属性值 OliveExcel androidtheme
    Android的Theme是由各种attr组合而成, 每个attr对应了这个属性的一个引用, 这个引用又可以是各种东西.   在某些情况下, 我们需要获取非自定义的主题下某个属性的内容 (比如拿到系统默认的配色colorAccent), 操作方式举例一则: int defaultColor = 0xFF000000; int[] attrsArray = { andorid.r.
  • 基于Zookeeper的分布式共享锁 roadrunners zookeeper分布式共享锁
    首先，说说我们的场景，订单服务是做成集群的，当两个以上结点同时收到一个相同订单的创建指令，这时并发就产生了，系统就会重复创建订单。等等......场景。这时，分布式共享锁就闪亮登场了。   共享锁在同一个进程中是很容易实现的，但在跨进程或者在不同Server之间就不好实现了。Zookeeper就很容易实现。具体的实现原理官网和其它网站也有翻译，这里就不在赘述了。   官
  • 两个容易被忽略的MySQL知识 tomcat_oracle mysql
    1、varchar(5)可以存储多少个汉字，多少个字母数字？ 　　相信有好多人应该跟我一样，对这个已经很熟悉了，根据经验我们能很快的做出决定，比如说用varchar(200)去存储url等等，但是，即使你用了很多次也很熟悉了，也有可能对上面的问题做出错误的回答。 　　这个问题我查了好多资料，有的人说是可以存储5个字符，2.5个汉字（每个汉字占用两个字节的话），有的人说这个要区分版本，5.0
  • zoj 3827 Information Entropy(水题) 阿尔萨斯 format
    题目链接：zoj 3827 Information Entropy 题目大意：三种底，计算和。 解题思路：调用库函数就可以直接算了，不过要注意Pi = 0的时候，不过它题目里居然也讲了。。。limp→0+plogb(p)=0，因为p是logp的高阶。 #include <cstdio> #include <cstring> #include <cmath&
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他