给定Employee 表 如下
| id | name | position | age |
|---|---|---|---|
| 94002 | John | Sales Manager | 32 |
| 95212 | Jane | Admin Manager | 39 |
| 96341 | John | Admin Secretary | 32 |
| 91234 | Jane | Admin Secretary | 21 |
对于查询语句:
select distinct name, age from Employee;
投影操作的结果为:
(Jane, 21)
(Jane, 39)
(John, 32)
其中 重复元组 (e.g. (John,32)) 被消除。
综上, 我们总结 Projection operation 投影操作 的三步骤:
step 1: scan 操作, 把整个关系表作为输入
step 2: 元祖属性操作, 比如, 去除无关属性,构造新属性 ...
step 3: 消除重复元组 (如果有 distinct), 两种实现: sort-based 和 hash-based
Sort-based Projection 基于排序的投影操作
基于 排序的投影操作需要一个临时的表来存储中间排序结果。
***** 1. 先把 R表 写入一个 temp 表中
for each tuple T in Rel {
T' = mkTuple([attrs],T)
write T' to Temp
}
***** 2. 在temp中, 根据 排序属性进行排序
sort Temp on [attrs]
**** 3. 去重
for each tuple T in Temp {
if (T == Prev) continue
write T to Result
Prev = T
}
例题:
Consider a table R(x,y,z) with tuples:
Page 0: (1,1,'a') (11,2,'a') (3,3,'c')
Page 1: (13,5,'c') (2,6,'b') (9,4,'a')
Page 2: (6,2,'a') (17,7,'a') (7,3,'b')
Page 3: (14,6,'a') (8,4,'c') (5,2,'b')
Page 4: (10,1,'b') (15,5,'b') (12,6,'b')
Page 5: (4,2,'a') (16,9,'c') (18,8,'c')
SQL: create T as (select distinct y from R)
Assuming:
3 memory buffers, 2 for input, one for output
pages/buffers hold 3 R tuples ,6 T tuples
Show how sort-based projection would execute this statement.
------------------------------------------------------
Temp(y)
buffer 0 : 1, 2, 3, 5, 6, 4 --> 1,2,3,4,5,6
buffer 1 : 2,7,3,6,4,2 --> 2,2,3,4,6,7
buffer 2: 1,5,6,2,9,8 --> 1,2,5,6,8,9
sorting...
buffer 0 :1,1,2,2,2,2
buffer 1 :3,3,4,4,5,5
buffer 2: 6,6,6,7,8,9
distinct and write into result:
buffer 0 : 1,2,3,4,5,6
buffer 1: 7,8,9
cost = scan R + write temp + sorting R + remove duplicates + write result
Cost of sort-based Projection
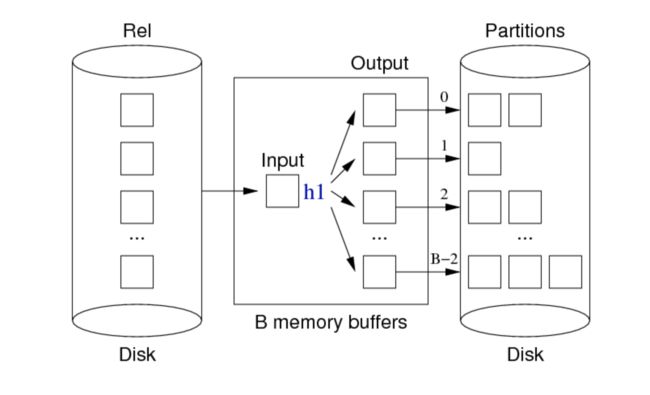
Hash-based Projection 基于散列的投影操作
-
Partitioning phase:散列 子表
-
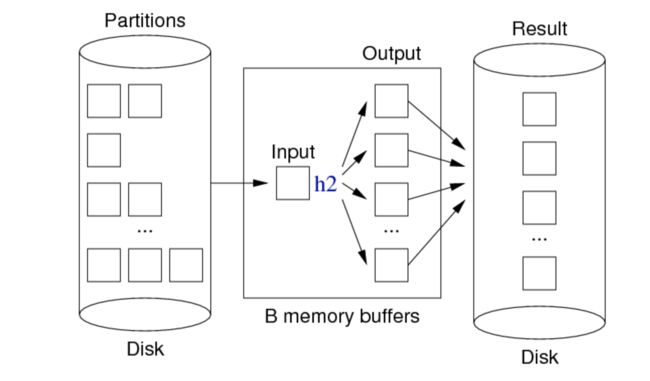
Duplicate elimination phase: 子表去重
for each tuple T in relation Rel {
T' = mkTuple([attrs],T)
H = h1(T', n)
B = buffer for partition[H]
if (B full) write and clear B
insert T' into B
}
for each partition P in 0..n-1 {
for each tuple T in partition P {
H = h2(T, n)
B = buffer for hash value H
if (T not in B) insert T into B
// assumes B never gets full
}
write and clear all buffers
}
例题:
Consider a table R(x,y,z) with tuples:
Page 0: (1,1,'a') (11,2,'a') (3,3,'c')
Page 1: (13,5,'c') (2,6,'b') (9,4,'a')
Page 2: (6,2,'a') (17,7,'a') (7,3,'b')
Page 3: (14,6,'a') (8,4,'c') (5,2,'b')
Page 4: (10,1,'b') (15,5,'b') (12,6,'b')
Page 5: (4,2,'a') (16,9,'c') (18,8,'c')
-- and then the same tuples repeated for pages 6-11
SQL: create T as (select distinct y from R)
Assuming:
4 memory buffers, one for input, 3 for partitioning
pages/buffers hold 3 R tuples (i.e. cR=3), 4 T tuples (i.e. cT=4)
hash functions: h1(x) = x%3, h2(x) = (x%4)%3
Show how hash-based projection would execute this statement.
------------------------------------------------------------------------------
Answer:
Inputs (k values):
1 2 3 5 6 4 2 7 3 6 4 2 1 5 6 2 9 8
1 2 3 5 6 4 2 7 3 6 4 2 1 5 6 2 9 8
1. partition h1(x) = x%3
P0 (via Buf[0]) 3 6 3 6 6 9 3 6 3 6 6 9
P1 (via Buf[1]) 1 4 7 4 1 1 4 7 4 1
P2 (via Buf[2]) 2 5 2 2 5 2 8 2 5 2 2 5 2 8
2. reomve duplicate h2(k) = (k % 4) % 3
P0 3 6 3 6 6 9 3 6 3 6 6 9
B0 3
B1 9
B2 6
---
P1 1 4 7 4 1 1 4 7 4 1
B0 4 7
B1 1
B2 ?
---
P2 2 5 2 2 5 2 8 2 5 2 2 5 2 8
B0 8
B1 5
B2 2
cost of hash-based Projection
- Scan R
- partition and duplicate : 2 b_p
- write result: b_out
total: b_R + 2 b_p + b_out
Index-only Projection 基于索引的投影操作
如果投影属性有索引,那么不需要 access 数据 就可以完成投影操作。