cf题面
洛谷题面
题解:
将所有1连出的边(我们称之为“关键边”)删掉,得到若干个连通块。
由于1号节点不会包含在 \(\geq\) 4的环里,
如果我们单独考虑一个连通块,那么它只可能是下面两种情况之一(这里套用了cf官方题解的图):

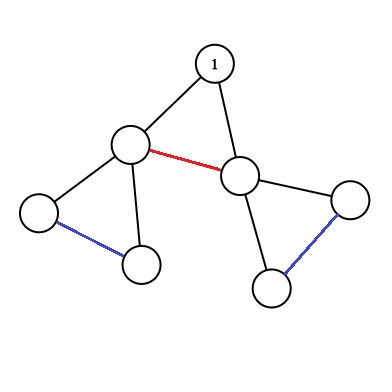
现在考虑题目的限制条件:
一个连通块满足条件的充要条件是:连通块里的所有环对应的边权异或和都能插入一个线性基里。
证明?众所周知,线性基里的数亦或起来不能为0。(不知道的请百度)
然后再回过头来看上述的两种连通块:
第一种:只有1条关键边,那么只有两种贡献:
1.空的线性基(删掉);2.下面连通块得到的线性基(不删)。
第二种:2条关键边,所以有3种情况:
1.空的线性基(删掉);2.下面连通块得到的线性基(删一条边);
3.下面连通块+包含红边的那个环得到的线性基。
接下来考虑合并这些贡献。
由于\(w\)在二进制下只有5位,本质不同的5位的线性基个数只有374个,
所以我们可以把这些合法的线性基都预处理出来,并将每个线性基表示为一个状态。
设 \(f_{i,j}\) 表示前\(i\)个连通块,合并后得到线性基\(j\)的方案数。
转移时一个一个把贡献合并上去就好。(合并就是线性基的合并)
注意到不同的线性基可能本质相同,我们需要让线性基唯一,这个可以参考一下我的insert函数:
IN insert(int *a,int x){
FOR(i,4,0){
if(!x)return 0;
if(!((x>>i)&1))continue;
if(!a[i]){
a[i]=x;
FOR(j,i-1,0)if((a[i]>>j)&1)a[i]^=a[j];
F(j,i+1,4)if((a[j]>>i)&1)a[j]^=a[i];
return 1;
}
x^=a[i];
}
return 0;
} 大概就是如果这一位是1并且有这一位的线性基,就把这个1消掉。
DP数组可以滚动优化。
时间复杂度:O(374* \(log_w\) +(n+m) \(log_w\) +374*n)
代码:
#include
using namespace std;
#define re register int
#define F(x,y,z) for(re x=y;x<=z;x++)
#define FOR(x,y,z) for(re x=y;x>=z;x--)
typedef long long ll;
#define I inline void
#define IN inline int
#define C(x,y) memset(x,y,sizeof(x))
#define STS system("pause")
templateI read(D &res){
res=0;register D g=1;register char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')g=-1;
ch=getchar();
}
while(isdigit(ch)){
res=(res<<3)+(res<<1)+(ch^48);
ch=getchar();
}
res*=g;
}
const int Mod=1e9+7;
IN insert(int *a,int x){
FOR(i,4,0){
if(!x)return 0;
if(!((x>>i)&1))continue;
if(!a[i]){
a[i]=x;
FOR(j,i-1,0)if((a[i]>>j)&1)a[i]^=a[j];
F(j,i+1,4)if((a[j]>>i)&1)a[j]^=a[i];
return 1;
}
x^=a[i];
}
return 0;
}
struct B{
int b[6];
friend bool operator < (B x,B y){
F(i,0,4)if(x.b[i]!=y.b[i])return x.b[i]mp;
struct E{
int to,nt,w;
}e[202000];
#define T e[k].to
int n,m,sn,ans,cnt,X,Y,W,tot,sum,c[440][440],val[101000],dep[101000],head[101000],t[6],vis[101000],f[101000][440];
I Add(int &x,int y){
(x+=y)>=Mod?x-=Mod:0;
}
IN rnk(B a){
//cout<>1;
if(a==bas[mid])return mid;
if(a