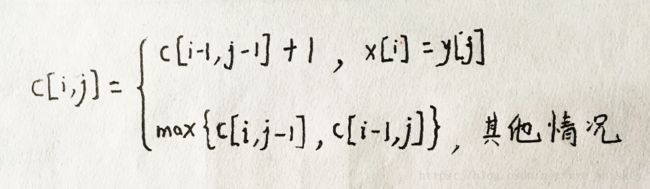动态规划、贪心算法区别

本文整理自MIT算法导论公开课

1. 动态规划（Dynamic progamming）

动态规划是一种设计技巧，而不是一种特定的算法，就像分治法一样。

最长公共子序列问题（Longest common subsequence）--经典动态规划例题

有两个序列，序列x[1_{m]，序列y[1}n]，找到它们的最长公共子序列，子序列不需要在原序列中占用连续的位置（最长公共子串要求连续），子序列可能不唯一。

Ex：
x：A B C B D A B
y：B D C A B A
公共子序列：BDAB BCAB BCBA（LCS(x,y)） LCS代表x,y的最长公共子序列

穷举法

检查x[1_{m]的每个子序列在y[1}n]中也是否存在，找到其中最长的。
运行时间分析：
检查是否存在代价为O(n)
x中的子序列数量为2^m，可以用一个m位的向量来表示，1表示选取那个字符，0表示不选取那个字符。
总运行时间为O(n·2^m)，指数级的运行时间是非常慢的。

动态规划策略

考虑序列x和y的前缀序列。
定义c[i,j]=|LCS(x[1,i],y[1,j])|，则有c[m,n]=|LCS(x,y)|。
动态规划递归方程：

image

递归实现动态规划

LCS(x,y,i,j)//忽略基本情况
if x[i]=y[j]
    c[i,j] ← LCS(x,y,i-1,j-1)+1
else
    c[i,j] ← max{LCS(x,y,i-1,j), LCS(x,y,i,j-1)}
return c[i,j]

在最长公共子序列问题中，可以发现在递归树中有很多相同的子问题，可分析得独立子问题得数量为m·n。

备忘录递归实现动态规划

LCS(x,y,i,j) //忽略基本情况
if c[i,j]=nil
    if x[i]=y[j]
        c[i,j] ← LCS(x,y,i-1,j-1)+1
    else
        c[i,j] ← max{LCS(x,y,i-1,j), LCS(x,y,i,j-1)}
return c[i,j]

最后得出动态规划问题满足的两个特性：

最优子结构，问题的最优解包含了子问题的最优解
重叠子问题，一个递归过程包含一些数量的独立的子问题被重复计算量多次

2. 贪心算法(Greedy algorithms)

最小生成树问题(MST)

世界上最重要的算法之一，在分布式系统中体现的价值尤为重要。
问题描述：输入的数据化为一个连通的无向图G=(V,E)和一个用于给每一条边加上一个实数权值的加权函数w(为了简化描述，下面的分析过程基于边的权值都不同的假设)，输出的结果为一个生成树T，并且它具有最小的权值和。

image.png

MST动态规划分析

最优子结构
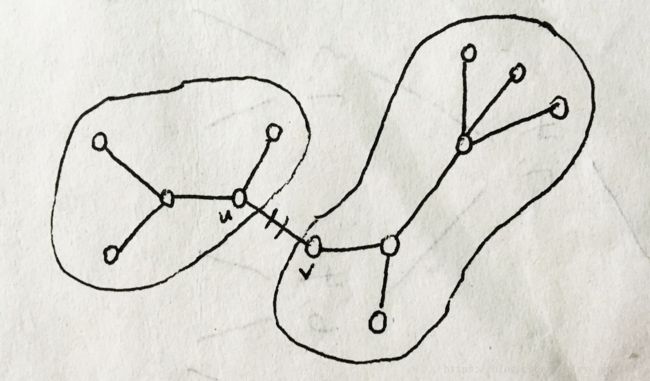
最小生成树MST T（图的其他边都被忽略）：

image

删除(u,v)∈T，那么最小生成树T被分为两个子树T1和T2。
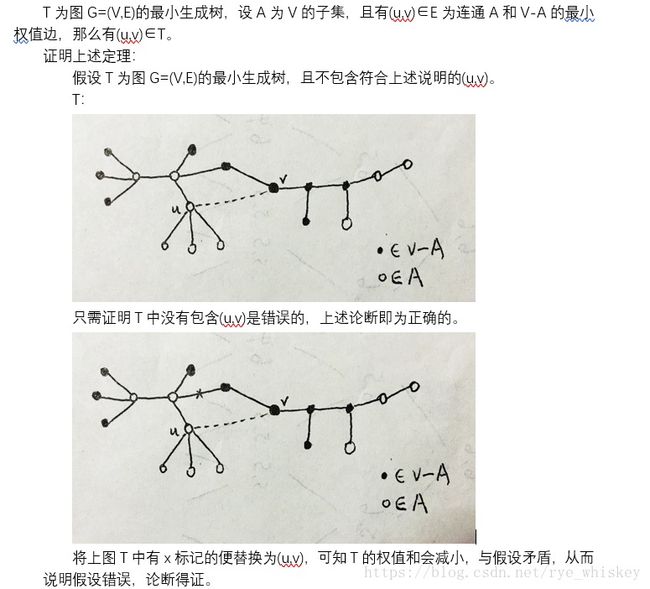
证明定理：
设图G1=(V1,E1)为原图G的一个子图，且满足V1为T1中的所有顶点，而边集E1={(x,y)∈E,x,y∈V1}，那么T1为G1的最小生成树（同理T2也有这样的结果）。
剪贴法（Cut & Paste）:
W(T)=w(u,v)+W(T1)+W(T2)
假设图G1有个比T1权值和更小的生成树T1‘，那么显然，就会有 W(T)=w(u,v)+W(T1’)+W(T2)，与W(T)=w(u,v)+W(T1)+W(T2)相矛盾，所以假设不成立，上述定理得证。
重叠子问题分析：
在删除(u,v)划分子树的过程中，不同的删除顺序中划分出相同的子树。
最小生成树问题具有重叠子问题。
综上可知，最小生成树可以使用动态规划。

贪心算法分析

贪心算法

Prim算法

image

贪心算法特性：

最优子结构，问题的最优解包含了子问题的最优解;
问题中存在一个局部最优解同时也是全局最优解!

贪心算法的关键不在于想到，而在于正确性的证明。要证明一个贪心算法是正确的，需要证明我们可以把一个最优解逐步转化为我们用贪心算法所得到的解，而解不会更差，从而证明贪心算法得到的解和最优解是一样好的（显然，最优解不可能更好)。而要证明一个贪心算法是错误的，只需要找到一个反例就可以了。

3.贪心和动态规划算法的比较：

动态规划和贪心算法都是一种递推算法
均有局部最优解来推导全局最优解

不同点：

贪心算法：

1.贪心算法中，作出的每步贪心决策都无法改变，因为贪心策略是由上一步的最优解推导下一步的最优解，而上一部之前的最优解则不作保留。
2.由（1）中的介绍，可以知道贪心法正确的条件是：每一步的最优解一定包含上一步的最优解。

动态规划算法：

1.全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解
2.动态规划的关键是状态转移方程，即如何由以求出的局部最优解来推导全局最优解
3.边界条件：即最简单的，可以直接得出的局部最优解

贪心算法与动态规划

贪心法的基本思路：
从问题的某一个初始解出发逐步逼近给定的目标，以尽可能快的地求得更好的解。当达到某算法中的某一步不能再继续前进时，算法停止。
该算法存在问题：
1. 不能保证求得的最后解是最佳的；
2. 不能用来求最大或最小解问题；
3. 只能求满足某些约束条件的可行解的范围。实现该算法的过程：
从问题的某一初始解出发；
while 能朝给定总目标前进一步 do
求出可行解的一个解元素；
由所有解元素组合成问题的一个可行解
贪心算法最经典的例子，给钱问题。
比如中国的货币，只看元，有1元2元5元10元20、50、100
如果我要16元，可以拿16个1元，8个2元，但是怎么最少呢？
如果用贪心算，就是我每一次拿那张可能拿的最大的。
比如16，我第一次拿20拿不起，拿10元，OK，剩下6元，再拿个5元，剩下1元
也就是3张 10、5、1。

每次拿能拿的最大的，就是贪心。

但是一定注意，贪心得到的并不是最优解，也就是说用贪心不一定是拿的最少的张数
贪心只能得到一个比较好的解，而且贪心算法很好想得到。
再注意，为什么我们的钱可以用贪心呢？因为我们国家的钱的大小设计，正好可以使得贪心算法算出来的是最优解（一般是个国家的钱币都应该这么设计）。如果设计成别的样子情况就不同了
比如某国的钱币分为 1元3元4元
如果要拿6元钱怎么拿？贪心的话先拿4 再拿两个1 一共3张钱
实际最优呢？两张3元就够了

求最优解的问题，从根本上说是一种对解空间的遍历。最直接的暴力分析容易得到，最优解的解空间通常都是以指数阶增长，因此暴力穷举都是不可行的。
最优解问题大部分都可以拆分成一个个的子问题，把解空间的遍历视作对子问题树的遍历，则以某种形式对树整个的遍历一遍就可以求出最优解，如上面的分析，这是不可行的。

贪心和动态规划本质上是对子问题树的一种修剪。两种算法要求问题都具有的一个性质就是“子问题最优性”。即，组成最优解的每一个子问题的解，对于这个子问题本身肯定也是最优的。如果以自顶向下的方向看问题树（原问题作根），则，我们每次只需要向下遍历代表最优解的子树就可以保证会得到整体的最优解。形象一点说，可以简单的用一个值（最优值）代表整个子树，而不用去求出这个子树所可能代表的所有值。

动态规划方法代表了这一类问题的一般解法。我们自底向上（从叶子向根）构造子问题的解，对每一个子树的根，求出下面每一个叶子的值，并且以其中的最优值作为自身的值，其它的值舍弃。动态规划的代价就取决于可选择的数目（树的叉数）和子问题的的数目（树的节点数，或者是树的高度？）。

贪心算法是动态规划方法的一个特例。贪心特在，可以证明，每一个子树的根的值不取决于下面叶子的值，而只取决于当前问题的状况。换句话说，不需要知道一个节点所有子树的情况，就可以求出这个节点的值。通常这个值都是对于当前的问题情况下，显而易见的“最优”情况。因此用“贪心”来描述这个算法的本质。由于贪心算法的这个特性，它对解空间树的遍历不需要自底向上，而只需要自根开始，选择最优的路，一直走到底就可以了。这样，与动态规划相比，它的代价只取决于子问题的数目，而选择数目总为1。